北京市清华大学附属中学望京学校2023-2024学年七年级下学期期中数学试题(无答案)

这是一份北京市清华大学附属中学望京学校2023-2024学年七年级下学期期中数学试题(无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
满分：100分考试时间：90分钟
一、选择题（每题3分，共24分）
1．在平面直角坐标系中，点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2．下列实数：，，（相邻两个1之间0的个数逐次加1），，3.14，中，无理数的个数是（ ）
A．1个B．2个C．3个D．4个
3．下列运算正确的是（ ）
A．B．C．D．
4．已知方程组，则的值是（ ）
A．2B．C．0D．
5．下列命题中，真命题是（ ）
A．同位角相等B．互补的角是邻补角
C．带根号的数一定是无理数D．对顶角相等
6．如图，O为直线上一点，平分，于点O，若，则的度数是（ ）
A．B．C．D．
7．光线在不同介质中的传播速度不同，因此当光线从水中射向空气时，要发生折射．由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图，当，时，和的度数分别是（ ）
A．，B．，C．，D．，
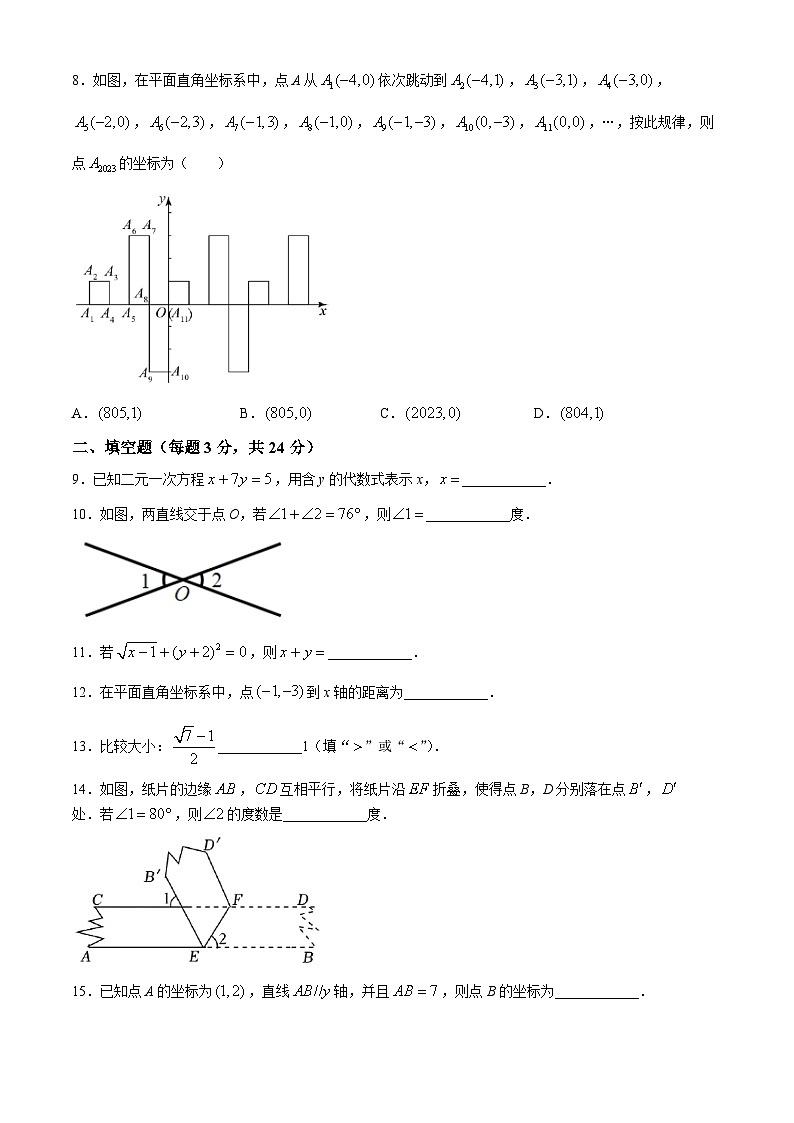
8．如图，在平面直角坐标系中，点A从依次跳动到，，，，，，，，，，…，按此规律，则点的坐标为（ ）
A．B．C．D．
二、填空题（每题3分，共24分）
9．已知二元一次方程，用含y的代数式表示x，____________．
10．如图，两直线交于点O，若，则____________度．
11．若，则____________．
12．在平面直角坐标系中，点到x轴的距离为____________．
13．比较大小：____________1（填“”或“”）．
14．如图，纸片的边缘，互相平行，将纸片沿折叠，使得点B，D分别落在点，处．若，则的度数是____________度．
15．已知点A的坐标为，直线轴，并且，则点B的坐标为____________．
16．三名快递员某天的工作情况如图所示，其中点，，的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数；点，，的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数．
有如下三个结论：
①上午派送快递所用时间最短的是甲；
②下午派送快递件数最多的是丙；
③在这一天中派送快递总件数最多的是乙．
上述结论中，所有正确结论的序号是____________．
三、解答题（17题，22题，23题，24题，25题每题5分，18题，20题，21题每题4分，19题3分，26题，27题每题6分，共52分）
17．计算：
18．解方程组：
19．求出下列式子中x的值：
20．完成下面的证明．已知：如图，，，．求证：平分．
证明：∵，，
∴，．（____________）
∴．
∴____________．（____________）
∴．（两直线平行，同位角相等）
．（____________）
∵，
∴．
∴平分．
21．如图所示的是天安门周围的景点分布示意图，若以正东、正北方向为x轴、y轴的正方向建立坐标系，表示电报大楼的点的坐标为，表示王府井的点的坐标为，请解决下面的问题：
（1）在图中画出相应的平面直角坐标系，并写出美术馆的坐标____________；
（2）“天安门—故宫—景山”所在的直线称为北京城的中轴线，在王府井的小奇同学如果要在最短的时间内（速度相同）赶到中轴线上，则小奇应该直接到达中轴线上的点的坐标为____________，理论依据为____________．
22．已知：用2辆A型车和1辆B型车载满货物一次可运货10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨，某物流公司现有26吨货物，计划A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．
根据以上信息，解答下列问题：
（1）1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨？
（2）请你帮该物流公司设计租车方案；
（3）若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱车方案，并求出最少租车费．
23．如图，在平面直角坐标系中，三角形三个顶点的坐标分别是，，，将三角形向左平移5个单位长度，再向上平移4个单位长度得到三角形，点A，B，C对应点分别为，，．
（1）点的坐标为____________；
（2）①画出三角形；
②三角形的面积为____________；
（3）若y轴上有一点Q，使得三角形的面积为4，则点Q的纵坐标为____________．
24．如图，点O在直线上，，与互余．
（1）求证：；
（2）平分交于点F，若，补全图形，并求的度数．
25．阅读探索：
小明在解方程组时发现若设，，
则方程组可变为，解此方程组得：，
即，所以．
（1）请你模仿运用上述方法解下列方程组；
（2）若已知关于x、y的方程组的解是，请直接写出关于m、n的方程组的解．
26．已知直线，点A是直线上一个定点，点B在直线上运动．点H为平面上一点，且满足．设．
（1）如图1，当时，____________；
（2）过点H作直线l平分，直线l交直线于点C．
①如图2，当时，求的度数；
②当时，直接写出的值．
27．在平面直角坐标系中，对于任意三个点A、B、C我们给出如下定义：“横长”a是指三点中横坐标的最大值与最小值的差，“纵长”b是指三点中纵坐标的最大值与最小值的差，若三个点的横长与纵长相等，我们称这三点为正方点．例如：已知点，点，点，观察并计算A、B、C三点的“横长”，A、B、C三点的“纵长”，因为，所以A、B、C三点为正方点．
（1）在点，，中，能与点A、B为正方点的是____________；
（2）点为y轴上一动点，若A，B，P三点为正方点，则t的值为____________；
（3）已知点D坐标是．平面直角坐标系中的点E满足以下条件：点A，D，E三点是横、纵长都为3的正方点，请在平面直角坐标系中画出所有符合条件的点E组成的图形．