

2020-2021学年第二学期期末教学质量检测八年级下册人教版数学试卷(二)(word版 含答案)
展开绝密★启用前
2020-2021学年第二学期期末教学质量检测(二)
八年级数学试题
满分150考试时间120分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.下列命题正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.有一个角是60°的等腰三角形是等边三角形
C.有一组邻边相等的四边形是菱形
D.对角线相等的四边形是矩形
2.如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的动点,试求PD+PA和的最小值是( )
A.2 B. C.2 D.6
3.若分式有意义,则x的取值应该该满足( )
A.x= B.x= C.x≠ D.x≠
4.使二次根式有意义的a的取值范围是( )
A. B. C. D.a≤5
5.下列各组数是勾股数的是( )
A.3,4,5 B.1.5,2,2.5 C.32,42,52 D.,,
6.下列计算中,正确的是( )
A. B.
C. D.
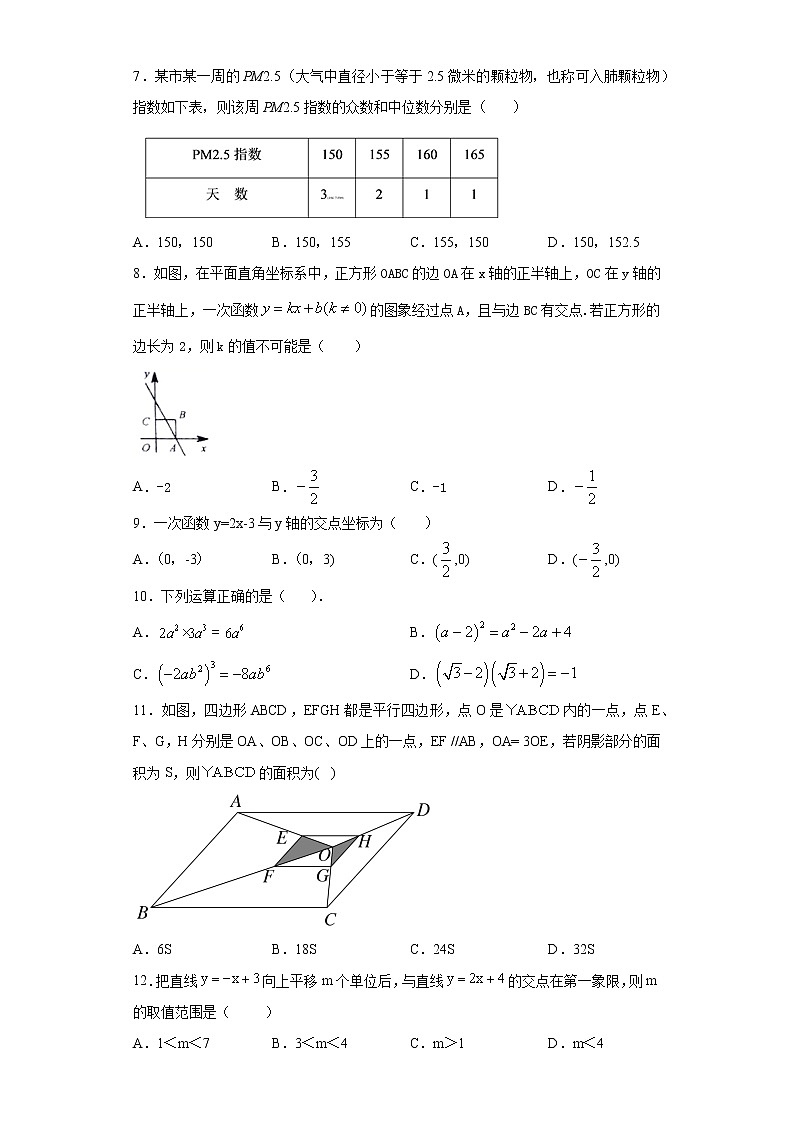
7.某市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物)指数如下表,则该周PM2.5指数的众数和中位数分别是( )
A.150,150 B.150,155 C.155,150 D.150,152.5
8.如图,在平面直角坐标系中,正方形OABC的边OA在x轴的正半轴上,OC在y轴的正半轴上,一次函数的图象经过点A,且与边BC有交点.若正方形的边长为2,则k的值不可能是( )
A.-2 B. C.-1 D.
9.一次函数y=2x-3与y轴的交点坐标为( )
A.(0,-3) B.(0,3) C.(,0) D.(,0)
10.下列运算正确的是( ).
A. B.
C. D.
11.如图,四边形ABCD,EFGH都是平行四边形,点O是内的一点,点E、F、G,H分别是OA、OB、OC、OD上的一点,EF //AB,OA= 3OE,若阴影部分的面积为S,则的面积为( )
A.6S B.18S C.24S D.32S
12.把直线向上平移m个单位后,与直线的交点在第一象限,则m的取值范围是( )
A.1<m<7 B.3<m<4 C.m>1 D.m<4
第II卷(非选择题)
二、填空题
13.如图,在四边形ABCD中,,,,,AB⊥BC,四边形ABCD的面积为___________________.
14.如图,已知一次函数的图像经过点A(5,0)与B(0,-4),那么关于的不等式﹤0的解集是_______.
15.在四边形中,,且,则四边形是______.
16.若关于x的不等式组有且只有四个整数解,且一次函数y=(k+3)x+k+5的图象不经过第三象限,则符合题意的整数k为___.
17.函数中,自变量x的取值范围是_____.
18.请写出任意一组自己喜欢的勾股数:________________.
三、解答题
19.甲,乙两车从城出发前往城.在整个行程中,甲,乙两车都以匀速行驶,汽车离开城的距离与时刻的对应关系如图所示.
请根据相关信息,解答下列问题:
(Ⅰ)填表:
从城出发的时刻
到达城的时刻
甲
5:00
乙
9:00
(Ⅱ)填空:
①,两城的距离为__________;
②甲车的速度为__________,乙车的速度为__________;
③乙车追上甲车用了__________,此时两车离开城的距离是__________;
④当9:00时,甲乙两车相距__________;
⑤当甲车离开城时,甲车行驶了__________;
⑥当乙车出发行驶__________时,甲乙两车相距.
20.如图所示,点是线段的中点,,.
(1)如图1,若,求证是等边三角形;
(2)如图1,在(1)的条件下,若点在射线上,点在点右侧,且是等边三角形,的延长线交直线于点,求的长度;
(3)如图2,在(1)的条件下,若点在线段上,是等边三角形,且点沿着线段从点运动到点,点随之运动,求点的运动路径的长度.
21.已知等腰三角形的周长为24.
(1)求底边长y关于腰长x的函数表达式;(x为自变量)
(2)求自变量x的取值范围.
22.(1)计算:.
(2)计算:.
(3)先化简,再求值:,其中满足.
(4)解方程:.
23.如图,已知∠ABC+∠C=180°,BD平分∠ABC,AE与BD相交于点F,∠EFD=∠D,求证:AE∥BC.
24.某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目
测试成绩/分
甲
乙
丙
笔试
75
80
90
面试
93
70
68
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?
25.如图所示,A、B两个旅游点从2011年至2015年“清明小长假”期间的旅游人数变化情况分别用实线和虚线表示,请解答以下问题:
(1)B旅游点的旅游人数相对上一年,增长最快的是哪一年?
(2)求A、B两个旅游点从2011年到2015年旅游人数的平均数和方差,并从平均数和方差的角度,用一句话对这两个旅游点的情况进行评价;
(3)A旅游点现在的门票价格为每人80元,为保护旅游点环境和游客的安全,A旅游点的最佳接待人数为4万人. A旅游点决定提高门票价格来控制游客数量. 已知游客数量y(万人)与门票价格x(元)之间满足函数关系. 若要使A旅游点的游客人数不超过4万人,则门票价格至少应提高多少元?
参考答案
1.B
【分析】
根据平行四边形的判定、等边三角形的判定、菱形的判定、矩形的判定定理依次判断.
【详解】
A、一组对边平行且相等的四边形是平行四边形,故该项错误;
B、有一个角是60°的等腰三角形是等边三角形,故该项正确;
C、有一组邻边相等的平行四边形是菱形,故该项错误;
D、对角线相等的平行四边形是矩形,故该项错误;
故选:B.
【点睛】
此题考查命题正确与否,掌握平行四边形的判定、等边三角形的判定、菱形的判定、矩形的判定定理是解题的关键.
2.A
【分析】
根据题意作出D关于OB的对称点D′,则D′的坐标是(0,2).则PD+PA的最小值就是AD′的长,利用勾股定理进行计算即可求解.
【详解】
解:作出D关于OB的对称点D′,
则D′的坐标是(0,2).则PD+PA的最小值就是AD′的长.
则OD′=2,
因而AD′=.
则PD+PA和的最小值是2.
故选:A.
【点睛】
本题考查正方形的性质以及最短路线问题,根据题意正确作出P的位置以及运用勾股定理进行计算是解题的关键.
3.C
【分析】
由题意根据分式有意义的条件是分母不等于零列出不等式,解不等式即可得到答案.
【详解】
解:分式有意义,则2x﹣3≠0,
解得,x≠.
故选:C.
【点睛】
本题考查分式有意义的条件,熟练掌握分式有意义的条件即分母不等于零是解题的关键.
4.D
【分析】
根据二次根式的双重非负性,被开方数非负即得.
【详解】
解:由题意得,,
解得.
故选:D.
【点睛】
本题考查二次根式的有意义的条件,熟练掌握二次根式双重非负性是解题关键.
5.A
【详解】
试题解析:A、∵32+42=52,∴是勾股数,故此选项正确;
B、∵1.52+22=2.52,但不是正整数,∴不是勾股数,故此选项错误;
C、∵,∴不是勾股数,故此选项正确;
D、∵()2+()2≠()2,∴不是勾股数,故此选项错误;
故选A.
6.B
【分析】
根据二次根式的加减法则可判断A、D两项,根据二次根式的乘法法则可判断B项,根据算术平方根的定义可判断C项,进而可得答案.
【详解】
解:A、,故本选项计算错误,不符合题意;
B、,故本选项计算正确,符合题意;
C、,故本选项计算错误,不符合题意;
D、,故本选项计算错误,不符合题意;
故选:B.
【点睛】
本题主要考查了二次根式的运算,属于基础题型,熟练掌握二次根式的运算法则是解题的关键.
7.B
【解析】
试题解析:这组数据按照从小到大的顺序排列为:150,150,150,155,155,160,165,
则众数为:150,
中位数为:155.
故选B.
点睛:根据众数和中位数的概念求解.
8.D
【解析】
解:由题意可得:点A(2,0),点C(0,2),把点A,C代入解析式可得:2k+2=0,解得:k=-1,当过点A直线与线段CB的交点从C向B靠近时,k的值为负数,且越来越小,故k≤-1,故k的值不可能是.故选D.
9.A
【解析】
根据y轴上点的横坐标为0.代入直线y=2x-3,可得y=-3,所以与y轴的交点为(0,-3).
故选:A.
10.D
【分析】
根据单项式乘以单项式的运算法则计算可判断A;根据完全平方公式展开可判断B;根据积的乘方和幂的乘方运算可判断C;根据平方差公式的运算可判断D.
【详解】
解:A. ,原选项计算错误,故不符合题意;
B. ,原选项计算错误,故不符合题意;
C. ,原选项计算错误,故不符合题意;
D. ,计算正确,符合题意,
故选:D
【点睛】
此题主要考查了单项式乘以单项式、积的乘方和幂的乘方以及乘法公式,熟练掌握运算法则和乘法公式是解答此题的关键.
11.B
【分析】
过O点作OM⊥AB于点M,延长MO与CD交于点N,易得ON⊥CD,由平行四边形面积公式和三角形面积公式可推出S△OAB+S△OCD=,再由相似三角形面积比等于相似比的平方可得S△OEF=S△OAB,S△OGH=S△OCD,进而得出阴影部分面积与面积之间的关系,即可得出答案.
【详解】
如图,过O点作OM⊥AB于点M,延长MO与CD交于点N,
∵四边形ABCD是平行四边形
∴AB∥CD,AB=CD
∴ON⊥CD
∵S△OAB=,S△OCD=,
∴S△OAB+S△OCD==
∵EF∥AB
∴△OEF∽△OAB,
∴,
∴,即S△OEF=S△OAB,
∵四边形EFGH是平行四边形
∴EF∥GH,EF=GH
又∵EF∥AB,AB∥CD
∴GH∥CD
∴△OGH∽△OCD,
∴,即S△OGH=S△OCD,
∴阴影部分面积S=S△OEF+S△OGH=,
∴
故选B.
【点睛】
本题考查平行四边形的性质和相似三角形的性质,熟练掌握平行四边形的性质得到相似三角形,利用面积比等于相似比的平方建立关系式是解题的关键.
12.C
【分析】
直线向上平移m个单位后可得:,求出直线与直线的交点,再由此点在第一象限列不等式组可得出m的取值范围:
【详解】
解:直线向上平移m个单位后可得:,
联立两直线解析式得:,解得:.
∴交点坐标为.
∵交点在第一象限,
∴
解得:m>1.
故选C.
【点睛】
本题考查一次函数的平移及交点坐标,根据平面直角坐标系中各象限点的特征,判断其所在象限,四个象限的符号特征分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
13.
【分析】
连接AC,可知四边形ABCD的面积=S△ADC+S△ABC,由勾股定理的逆定理得到△ACD是一个直角三角形.则四边形面积可求.
【详解】
解:连接AC
在Rt△ABC中
AC=
∵在△ACD中, +12=52,
即AD2+CD2=AC2,
∴△ACD为直角三角形,
∴S四边形ABCD=S△ABC+S△ACD=AB•BC+AD•CD=×3×4+×2×1=6+.
故答案为:6+
【点睛】
本题考查了勾股定理和它的逆定理,解答关键是利用勾股定理逆定理找到并证明图中的直角三角形.
14.
【分析】
首先利用图象可找到图象在轴下方时,进而得到关于的不等式的解集是.
【详解】
由题意可得:一次函数中,时,图象在轴下方,,
则关于的不等式的解集是,
故答案为:.
【点睛】
本题主要考查了一次函数与一元一次不等式,关键是掌握数形结合思想.认真体会一次函数与一元一次不等式之间的内在联系.
15.平行四边形
【分析】
由,且可知AB∥DC,AB=DC,据此可判断四边形是平行四边形.
【详解】
解:∵,且,
∴AB∥DC,AB=DC,
∴四边形是平行四边形.
故答案是:平行四边形.
【点睛】
此题考查了平面向量的知识及平行四边形的判定.解此题的关键是证明一组对边平行且相等.
16.﹣4.
【解析】
【分析】
根据关于x不等式组 有且只有四个整数解得出k的取值范围,再由一次函数y=(k+3)x+k+5的图象不经过第三象限得出k取值范围,再找出其公共解集即可.
【详解】
解:解不等式组 ,
得,<x≤2,
∵不等式组有且只有四个整数解,
∴其整数解为:﹣1,0,1,2,
∴﹣2≤<﹣1,即﹣4≤k<﹣2.
∵一次函数y=(k+3)x+k+5的图象不经过第三象限,
∴,解得﹣5≤k<﹣3,
∴﹣4≤k<﹣3,
∴k的整数解只有﹣4.
故答案为:﹣4.
【点睛】
本题考查一次函数与一元一次不等式,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解题的关键.
17.x≠1
【分析】
根据分母不等于0,可以求出x的范围;
【详解】
解:(1)x-1≠0,解得:x≠1;
故答案是:x≠1,
【点睛】
考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
18.12,16,20(答案不唯一)
【解析】
由勾股数的定义:“若三个正整数满足,就说是一组勾股数.”可知勾股数很多,比如:12,16,20就是一组勾股数.
19.(Ⅰ)甲;10:00;乙;6:00;(Ⅱ)①300;②60,100;③1.5,150;④60;⑤2;⑥1或2
【分析】
(Ⅰ)根据时间与路程的图像即可进行填表;
(Ⅱ)①看图可以直接得出两城距离;
②根据图像可之甲用时5h走完全程300km,即可得出甲的速度,乙用时3h走完全程300km,得出乙的速度;
③根据图像可以知道乙车追上甲车时是7:30;此时乙追甲追了7:30-6:00=1.5h,此时两车离开城的距离用全程减去已走的路程即可得出;
④用两车行驶的路程相减即可得出路程差相距多少;
⑤用路程除以时间即可得出;
⑥这里要考虑乙追上甲之前以及乙追上甲以后的两种情况.
【详解】
(Ⅰ)看图进行填报即可,甲;10:00;乙;6:00;
(Ⅱ)①看图钟纵轴,两地距离300km;
②甲速:300(10:00-5:00)=3005=60(km/h),乙速:300(9:00-6:00)=100(km/h);
③乙追甲追了7:30-6:00=1.5h,乙所走路程即可得距离300-1001.5=150(km/h)
④9:00时,甲走了60(9-5)=240(km);甲乙两车相距300-240=60(km)
⑤用120km除以速度,12060=2h;
⑥设甲y=kx+b,则 , , y=60t-300
设乙y=mx+n,则,,y=100t-600
两车相距20km,设t时时,两车相距20km,
(60t-300)-(100t-600)=20或(100t-600)-(60t-300)=20或60t-300=280
解得t=7或8或,因为t为时间点,7-6=1h,8-6=2h,-6=3 >3(舍去)
所以符合条件的答案为:1或2
【点睛】
此题主要考查了一次函数图像的应用问题,结合行程问题进行分析,关键是正确从函数图像中得出正确的信息.
20.(1)证明见解析;(2)18;(3)18.
【分析】
(1)利用垂直平分线的性质可得BA=BC,再得,即可证明是等边三角形;
(2)证明,得出,继而得到,即可求得PC的长度;
(3)取BC的中点H,分两种情况证明,得出或,可知点N的运动路径是一条线段,据此求解即可.
【详解】
解:(1)∵,,
,
是线段中点,,
,
是等边三角形;
(2)∵、是等边三角形,
∴,AB=BC,BD=BQ,,
∴,
∴,
,
,
,
,
,
;
(3)取BC的中点H,连接OH,连接CN,
分两种情况讨论:
当M在线段上时,如图2,
∵H是BC的中点,,
∴,
∴是等边三角形,
∵是等边三角形,
∴,OM=ON, ,
∴,
∴,
点从起点到作直线运动,
∵当点M在点B时,CN=BH=9,
∴点M从B运动到H时,点N运动路径的长度等于9;
当点M在线段上时,如图3,
∵H是BC的中点,,
∴,
∴是等边三角形,
∵是等边三角形,
∴,OM=ON, ,
∴,
∴,
点从到终点作直线运动,
∵当点M在点C时,CN=CH=9,
∴点M从H运动到C时,点N运动路径的长度等于9;
综上所述,的路径长度为:.
【点睛】
本题考查了等边三角形的性质与判定及全等三角形的性质与判定,发现或构造全等三角形是解题的关键,本题难度较大,旨在培养学生综合运用所学知识解决复杂问题的能力.
21.(1);(2)
【分析】
(1)根据三角形周长公式即可求解;
(2)根据两边之和大于第三边,两边之差小于第三边列出不等式组即可求解.
【详解】
(1)由题意得,,
∴底边长y关于腰长x的函数表达式为:.
(2)根据三角形得三边关系可得不等式组:
解不等式组,得,
∴x得取值范围是.
【点睛】
本题考查了一次函数的应用,三角形的三边关系,在实际应用题型中一定要注意函数表达式的自变量取值范围.
22.(1);(2);(3),;(4)
【分析】
(1)(2)根据二次根式的乘法和加减法可以解答本题;
(3)根据分式的加减法和除法可以化简题目中的式子,然后将整体代入求值即可解答本题;
(4)根据解分式方程的方法,把分式方程化为整式方程,可以解答本题,注意验根.
【详解】
解:(1)原式=
=;
(2)原式=
=;
(3)原式=
=
=
=,
∵,
∴,
∴原式=
=;
(4)去分母,得,,
去括号,得,,
移项,得,,
合并同类项,得,,
系数化为1,得,,
检验:当时,,
∴是原方程的解.
【点睛】
本题考查了二次根式的混合运算、分式的化简求值以及解分式方程,解答本题的关键是明确它们各自的解答方法,注意分式方程要检验.
23.见解析.
【分析】
根据∠ABC+∠C=180°,可得AB∥CD,得∠ABD=∠D,再根据BD平分∠ABC,可得∠ABD=∠DBC,根据已知条件等量代换后得∠DBC=∠EFD,进而AE∥BC.
【详解】
证明:∵∠ABC+∠C=180°,
∴AB∥CD,
∴∠ABD=∠D,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠D=∠DBC,
∵∠EFD=∠D,
∴∠DBC=∠EFD,
∴AE∥BC.
【点睛】
本题主要考查平行线的性质与判定及角平分线的定义,熟练掌握知识点是解题的关键.
24.(1)a=25;甲民主评议的得分50(分);乙民主评议的得分是80(分);丙民主评议的得分是: 70(分)(2)丙会被选中.
【解析】
【分析】
(1)用1-40%-35%即可得到a的值,再分别用200乘以三人的得票率,求出三人民主评议的得分各是多少即可;
(2)根据加权平均数的计算方法列式计算,分别求出三人的得分各是多少;然后比较大小,判断出三人中谁的得分最高即可.
【详解】
(1)a%=1-40%-35%,所以a=25,
甲民主评议的得分是:200×25%=50(分);
乙民主评议的得分是:200×40%=80(分);
丙民主评议的得分是:200×35%=70(分);
(2)甲的成绩是:(75×4+93×3+50×3)÷(4+3+3)=729÷10=72.9(分),
乙的成绩是:(80×4+70×3+80×3)÷(4+3+3)=770÷10=77(分),
丙的成绩是:(90×4+68×3+70×3)÷(4+3+3)=774÷10=77.4(分),
∵77.4>77>72.9,∴丙的得分最高,将被选中.
25.(1)、2014;(2)、从2011至2015年清明小长假期间,A、B两个旅游点平均每年的旅游人数均为3万人,但A旅游点较B旅游点的旅游人数波动更大一些;(3)、20元.
【解析】
试题分析:(1)认真审图不难看出B旅游点的旅游人数相对上一年增长最快的是2004年;
(2)根据平均数和方差的计算公式求出甲乙的平均数与方差,然后根据方差的大小两个旅游点的情况进行评价;
(3)根据函数的解析式y=5-x100≤4来确定应提高票价多少元.
试题解析:(1)B旅游点的旅游人数相对上一年增长最快的是2004年;
(2)xA=1+2+3+4+55=3(万人),
xB=3+3+2+4+35=3(万人).
SA2=15[(1-3)2+(2-3)2+(3-3)2+(4-3)2+(5-3)2]=2,
SB2=15[(3-3)2+(3-3)2+(2-3)2+(4-3)2+(3-3)2]=25.
从2011至2015年清明小长假期间,A.B两个旅游点平均每年的旅游人数均为3万人,但A旅游点较B旅游点的旅游人数波动更大一些;
(3)由题意,得5-x100≤4,
解得x≥100,
x-80≥100-80=20.
答:A旅游点的门票至少要提高20元.
考点:1.一元一次不等式的应用;2.折线统计图;3.算术平均数;4.方差.
2020-2021学年人教版数学八年级下册期末综合检测试卷(word版 含答案): 这是一份2020-2021学年人教版数学八年级下册期末综合检测试卷(word版 含答案),共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年第二学期期末教学质量检测八年级下册人教版数学试卷(三)(word版 含答案): 这是一份2020-2021学年第二学期期末教学质量检测八年级下册人教版数学试卷(三)(word版 含答案),共23页。试卷主要包含了请将答案正确填写在答题卡上,下列计算正确的是,在平面直角坐标系中,已知点A,下列命题等内容,欢迎下载使用。
2020-2021学年第二学期期末教学质量检测八年级下册人教版数学试卷(四)(word版 含答案): 这是一份2020-2021学年第二学期期末教学质量检测八年级下册人教版数学试卷(四)(word版 含答案),共25页。试卷主要包含了请将答案正确填写在答题卡上,如图,直线,点A1,要使式子有意义,的取值范围是,下列能够成直角三角形的是,下列计算正确的是等内容,欢迎下载使用。












