

(海南省海口市专用)2021年中考数学考前押题卷(word版 含答案)
展开海口市2021年中考数学考前押题卷
一、选择题(本大题满分36分,每小题3分)在下列各题的四个备选答案中,有且只有一个是正确的.
1.(本题3分)一个正有理数在增大时,它的绝对值( ).
A.在减小 B.不变 C.在增大 D.不一定变
2.(本题3分)下列计算正确的是( )
A. B. C. D.
3.(本题3分)计算的结果是( )
A. B.x C.3 D.0
4.(本题3分)截止到4月18日0时,全球感染新型冠状病毒肺炎的人数已经突破人,“山川异域,风月同天”,携手抗“疫”,刻不容缓.将用科学记数法表示为( )
A. B. C. D.
5.(本题3分)某班体育课上老师记录了位女生分钟仰卧起坐的成绩(单位:个)分别为:,,,,,,,这组数据的中位数和众数分别是( )
A., B., C., D.,
6.(本题3分)下列各点在反比例函数图象上的是( )
A. B. C. D.
7.(本题3分)已知当x=2时,代数式ax3+bx+6的值是﹣7,则当x=﹣2时,代数式ax3+bx+6的值是( )
A.19 B.13 C.5 D.﹣19
8.(本题3分)不等式组的整数解为( )
A. B.5 C.3 D.3,4,5
9.(本题3分)如图所示,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为( )
A.22° B.28° C.32° D.38°
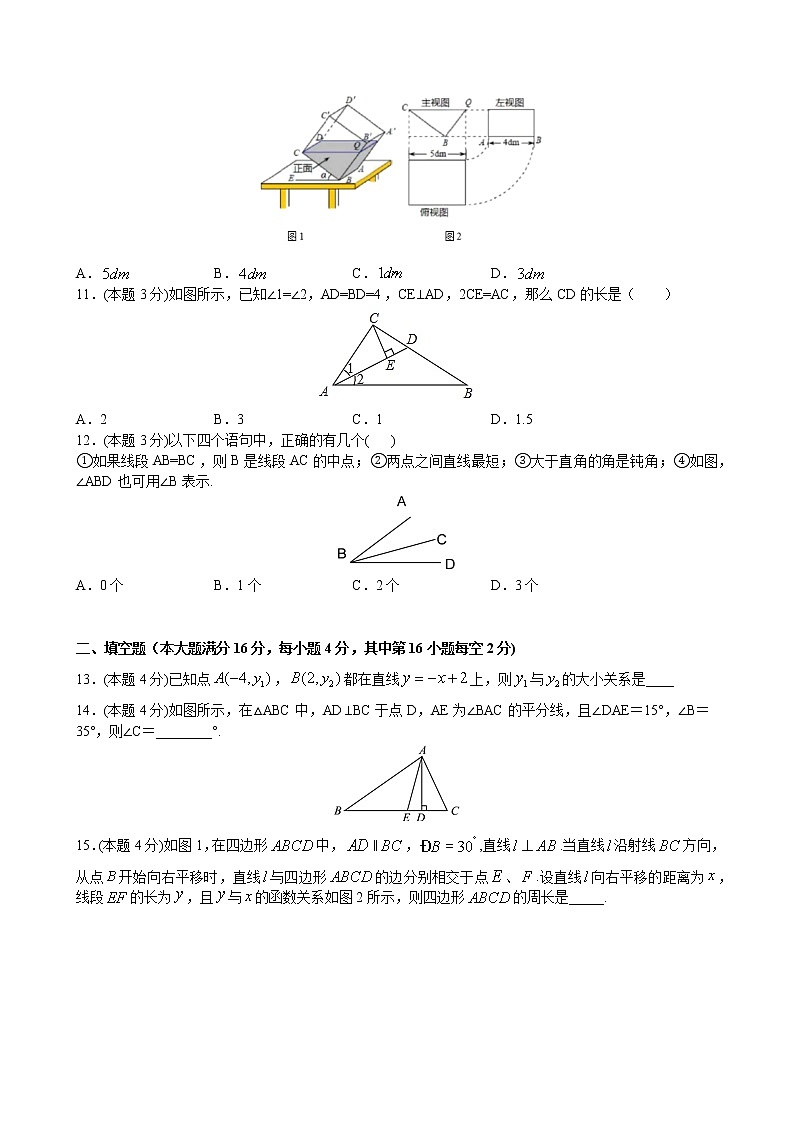
10.(本题3分)一透明的敞口正方体容器装有一些液体,棱始终在水平桌面上,容器底部的倾斜角为(,如图1所示).如图1,液面刚好过棱,并与棱交于点,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.则此时的长为( )
A. B. C. D.
11.(本题3分)如图所示,已知∠1=∠2,AD=BD=4,CE⊥AD,2CE=AC,那么CD的长是( )
A.2 B.3 C.1 D.1.5
12.(本题3分)以下四个语句中,正确的有几个( )
①如果线段AB=BC,则B是线段AC的中点;②两点之间直线最短;③大于直角的角是钝角;④如图,∠ABD也可用∠B表示.
A.0个 B.1个 C.2个 D.3个
二、填空题(本大题满分16分,每小题4分,其中第16小题每空2分)
13.(本题4分)已知点,都在直线上,则与的大小关系是____
14.(本题4分)如图所示,在△ABC中,AD⊥BC于点D,AE为∠BAC的平分线,且∠DAE=15°,∠B=35°,则∠C=________°.
15.(本题4分)如图1,在四边形中,∥,,直线.当直线沿射线方向,从点开始向右平移时,直线与四边形的边分别相交于点、.设直线向右平移的距离为,线段的长为,且与的函数关系如图2所示,则四边形的周长是_____.
16.(本题4分)在数轴上,点表示1,现将点沿轴做如下移动,第一次点向左移动3个单位长度到达,第二次将点向右移动6个单位长度到达点,第三次将点向左移动9个单位长度到达点,按照这种移动规律移动下去,第次移动到点,那么表示的数是____.
三、解答题(本大题满分68分)
17.(本题12分)计算:
(1)计算:
(2)化简:
18.(本题10分)某校运动会需购买、两种奖品.若购买种奖品3件和种奖品2件,共需60元;若购买种奖品5件和种关品3件,共需95元.
(1)求、两种奖品单价各是多少元?
(2)学校计划购买、两种奖品共100件,购买费用不超过1150元,且种奖品的数量不大于种奖品数量的3倍.设购买种奖品件,购买费用为元,写出(元)与(件)之间的函数表达式,并求最少费用的值.
19.(本题8分)2020年春节联欢晚会传承创新亮点多,收视率较往年大幅增长.成都高新区某学校对部分学生就2020年春晚的关注程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图(其中A表示“非常关注”;B表示“关注”;C表示“关注很少”;D表示“不关注”).
请你根据统计图中所提供的信息解答下列问题:
(1)直接写出m=______;估计该校1800名学生中“不关注”的人数是______人;
(2)在一次交流活动中,老师决定从本次调查回答“关注”的同学中随机选取2名同学来谈谈他们的想法,而本次调查回答“关注”的这些同学中只有一名男同学,请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率.
20.(本题10分)如图,小甬的家在某住宅楼的最顶层,他家对面有一建筑物,他很想知道建筑物的高度,他首先量出A到地面的距离()为,又测得从A处看建筑物底部C的俯角为,看建筑物顶部D的仰角为,且都与地面垂直,点A,B,C,D在同一平面内.
(1)求与之间的距离(结果保留根号).
(2)求建筑物的高度(结果精确到).
(参考数据:)
21.(本题13分)如图1,在正方形ABCD中,E、F分别为边AB、BC 的中点,连接AF、DE交于点G.
(1)求证:AF⊥DE;
(2)如图2,连接BG,求证:BG平分∠EGF;
(3)如图3,连接BD交AF于点H, 设ADG的面积为S,求证:BG2=2S.
22.(本题15分)已知:如图,直线交坐标轴于A、C两点,抛物线过A、C两点.
(1)求抛物线的解析式;
(2)若点P为抛物线位于第三象限上一动点,连接PA,PC,试问△PAC是否存在最大值,若存在,请求出△APC取最大值以及点P的坐标,若不存在,请说明理由;
(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.
参考答案
1.C
【解析】∵正有理数的绝对值=正有理数
∴正有理数在增大时,它的绝对值在增大
故选:C.
2.C
【解析】解:A、,故A错误;
B、,故B错误;
C、,故C正确;
D、,故D错误;
故选:C.
3.C
【解析】原式===3.
故选C.
4.D
【解析】=,
故选:D.
5.B
【解析】把这些数从小到大排列为:28,35,35,38,38,38,48,
最中间的数是38,
则中位数是38;
∵38出现了3次,出现的次数最多,
∴这组数据的众数是38;
故选B.
6.C
【解析】解:由,即,xy=-5,经排查只有C符合;
故答案为C.
7.A
【解析】∵当x=2时,代数式ax3+bx+6的值是-7,
∴8a+2b+6=-7,
∴8a+2b=-13,
当x=-2时,ax3+bx+6=-8a-2b+6=-(8a+2b)+6=-(-13)+6=13+6=19.
故选A.
8.D
【解析】解:
解不等式①,得:
解不等式②,得:
∴不等式组的解集为:
∴不等式组的整数解为:3,4,5
故选:D.
9.B
【解析】如图,
∵a∥b,
∴∠1=∠C=50°,
又∠1=∠A+∠B,
∴∠A=∠1-∠B=50°-22°=28°,
故选B.
10.D
【解析】解:根据题意,得CQ与BE的位置关系是:CQ∥BE,CQ=5,BC=AB=4,
在Rt△BCQ中,BQ==3(dm).
11.A
【解析】解:在Rt△AEC中,∵=,∴∠1=∠2=30°,
∵AD=BD=4,∴∠B=∠2=30°,∴∠ACD=180°﹣30°×3=90°,∴CD=AD=2.
故选A.
12.A
【解析】解:A中,错误,只是其中一种情况
B中,错误,两点之间线段最短
C中,错误,大于直角的角亦可以是平角
D中,错误,不可以,因为有数个表示法
故选A
13.y1>y2
【解析】解:∵点A(-4,y1)和点(2,y2)都在直线y=-x+2上,
∴y1=4+2=6,y2=-2+2=0,
∵6>0,
∴y1>y2.
故答案为:y1>y2.
14.65
【解析】∵∠DAE=15°,∠ADE=90°,
∴∠AED=90°-∠DAE=75°,
∴∠BAE=∠AED-∠B=75°-35°=40°,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=80°,
∴∠C=180°-∠B-∠BAC=65°,
故答案为65.
15.
【解析】由题意和图像易知BC=5,AD=7-4=3
当BE=4时(即F与A重合),EF=2
又∵且∠B=30°
∴AB=,
∵当F与A重合时,把CD平移到E点位置可得三角形AED′为正三角形
∴CD=2
∴AB+BC+CD+AD=+5+2+3=10+
故答案时.
16.-3029
【解析】第一次点A向左移动3个单位长度至点,则表示的数,1−3=−2;
第2次从点向右移动6个单位长度至点,则表示的数为−2+6=4;
第3次从点向左移动9个单位长度至点,则表示的数为4−9=−5;
第4次从点向右移动12个单位长度至点,则表示的数为−5+12=7;
第5次从点向左移动15个单位长度至点,则表示的数为7−15=−8;
…;
发现序号是奇数的点在负半轴上,
:−2,
:−5=−2+(−3)×1
:−8=−2+(−3)×2,
A2n+1:−2+(−3)×n
则点表示:−2−3×
故答案为:−3029.
17.(1);(2)
【解析】(1)原式=;
(2)原式=
18.(1)奖品的单价是10元,奖品的单价是15元.(2);1125.
【解析】(1)设奖品的单价是元,奖品的单价是元,由题意,得
,解得.
答:奖品的单价是10元,奖品的单价是15元.
(2)由题意得
,
且,解得,,
,,,
,
∵为整数,
,71,72,73,74,75,
,,
随的增大而减小,即当时,有最小值,
(元).
19.(1)25;330;(2).
【解析】解:(1)∵了解很少的有30人,占50%,
∴接受问卷调查的学生共有:30÷50%=60(人);
∴m%=×100%=25%,
该校1800名学生中“不关注”的人数是1800×=330(人);
故答案为:25,330;
(2)由题意列树状图:
由树状图可知,所有等可能的结果有12 种,选取到两名同学中刚好有这位男同学的结果有6种,
∴选取到两名同学中刚好有这位男同学的概率为=.
20.(1);(2)
【解析】解:(1)如图,作于M,
则四边形为矩形,,
∴,
在中,,
∴m,
∴与之间的距离是;
(2)在中,,
∴,
∴,
∴建筑物的高度约为.
21.(1)见解析;(2)见解析;(3)见解析
【解析】(1)∵四边形ABCD是正方形,
∴AD=AB=BC,∠DAE=∠ABF=90°,
∵E、F分别为边AB、BC 的中点,
∴AE=BF,
∴ΔDAE≌ΔABF,
∴∠ADE=∠BAF,
∵∠DAG+∠EAG=90°,
∴∠DAG+∠ADG=90°,
∴∠AGD=90°,
∴AF⊥DE;
(2)如图2,过点B作BM⊥AF,垂足为M,则BM//GE,
∵AE=BE,
∴AG=GM,
设BF=a,则AB=2a,AF=a,
∵,
∴,
∴BM=a,
∴AM==a,
∴GM=BM=a,
∴ΔBMG为等腰直角三角形,
∴∠BGM=45°,∠BGE=90°-45°=45°,
∴∠BGM=∠BGE,
∴BG平分∠EGF;
(3)ΔADG的面积为S,则AG·DG=2S,
过点B作BM⊥AF,垂足为M,
由(2)知:GM=AG,BM=AM,BG2=2BM2,
∵∠AGD=∠AMB=90°,∠ADG=∠BAM,AB=AD,
∴ΔDAG≌ΔABM,
∴BM=AG,AM=DG,
∴AG=DG,AG·DG=2AG2=2S,
即AG2=S ,
∴BM2=S,
∴BG2=2BM2=2S.
.
22.(1);(2)存在,△PAC的面积最大值为,点P的坐标为(,);(3)点M的坐标为:或或(,)或(,).
【解析】解:(1)交x轴于A(-3,0),交y轴于C(0,-3),
∵抛物线经过点A(-3,0),点C(0,-3),
∴,解得,
∴抛物线解析式为:;
(2)如图2,过点P作PQ⊥x轴,垂足为Q,直线PQ,AC交于点P,
设点P的坐标为(,),则点D的坐标为(,),
∴线段PD的长为:()-()=,
∵,,
∴====,
∵,∴当时候,△PAC的面积又最大值,最大值为,
此时点P的坐标为(,);
(3)①如图3,当点M在对称轴左侧时,构造矩形EFCG,设点M的坐标为(,),
∵△NMC是以∠NMC为直角的等腰直角三角形
∴∠NME+∠CMF=90°,∠FCM+∠CMF=90°
∴∠NME=∠FCM
又∵∠E=∠F=90°,MN=MC
∴△MEN≌△CFM,
∵抛物线的对称轴为直线x=-1,
∴MF==,NE=,
∵MF=NE,∴,
解得(舍),,
故点M的坐标为;
②如图6,作MF⊥y轴,垂足为F,MF交对称轴于点E;
设点M的坐标为(,),则ME= ,CF= ,
由①同理可证△MNE≌△CFM,
∵ME=CF,故,
解得:(舍),,
故点M的坐标为(,);
③如图5,当点M在对称轴的右侧时,过点M作EF∥x轴,分别交对称轴与y轴于点E和点F.
设点M的坐标为(,),
由①同理可证△MEN≌△MFC,抛物线对称轴为直线x=-1,
则ME= =,CF= = ,
∵ME=CF,∴,解得:(舍),,
故的点M的坐标 为;
④如图4,作ME⊥对称轴,垂足为E,ME交NC,交点为F.
设点M的坐标为(,),则ME= ,CF= ,
由①同理可证△MNE≌△CFM,
∵ME=CF,故,
解得:,(舍),
故点M的坐标为(,);
综上可得点M的坐标为:或或(,)或(,).













