2021年黑龙江省哈尔滨市松北区调研测试三数学试题（word版 含答案）

2021年初中毕业学年调研测试（三）

数学试卷

考生须知：

1.本试卷满分为120分，考试时间为120分钟。

2.答题前，考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚，将

“条形码”准确粘贴在条形码区域内。

3.请接照题号的顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草纸、试题纸上答题无效。

4.选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米的黑色字迹的签字笔书写，字体工整、笔迹清楚。

5.保持卡面整洁，不要折叠、不要弄脏、不要弄皱，不准使用涂改液、修正带、刮纸刀。

第Ⅰ卷选择题（共30分）（涂卡）

一、填空题（每题3分，共30分）

1.今年2月份某市一天的最高气温为10℃，最低气温为℃，那么这一天的最高气温比最低气温高（    ）

A.℃ B.17℃ C.5℃ D.11℃

2.下列各式中计算正确的是（    ）

A.  B.

C.  D.

3.下列图案中是中心对称图形但不是轴对称图形的是（    ）

A. B. C. D.

4.如图是由五个完全一样的正方体搭建而成的立体图形，它的主视图是（    ）

A. B. C. D.

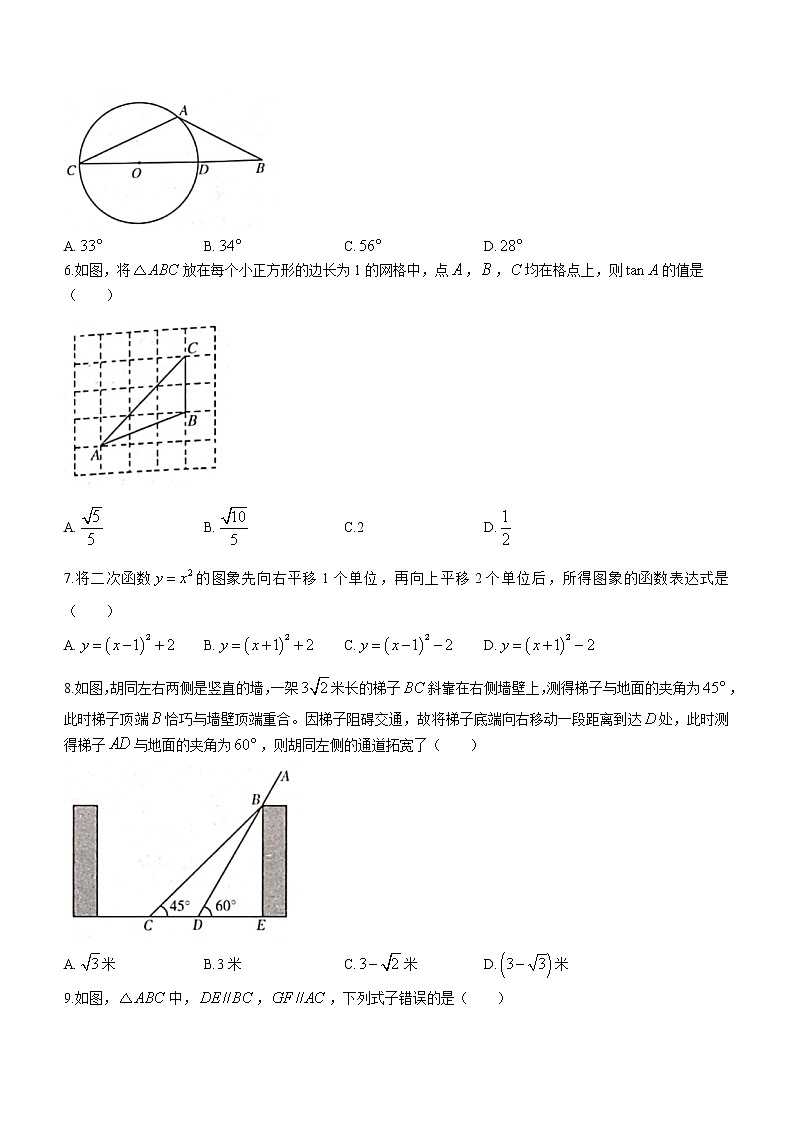
5.如图，为的切线，为弦，连接交于点，若经过圆心，，则的度数为（    ）

A. B. C. D.

6.如图，将放在每个小正方形的边长为1的网格中，点，，均在格点上，则的值是（    ）

A. B. C.2 D.

7.将二次函数的图象先向右平移1个单位，再向上平移2个单位后，所得图象的函数表达式是（    ）

A. B. C. D.

8.如图，胡同左右两侧是竖直的墙，一架米长的梯子斜靠在右侧墙壁上，测得梯子与地面的夹角为，此时梯子顶端恰巧与墙壁顶端重合。因梯子阻碍交通，故将梯子底端向右移动一段距离到达处，此时测得梯子与地面的夹角为，则胡同左侧的通道拓宽了（    ）

A.米 B.3米 C.米 D.米

9.如图，中，，，下列式子错误的是（    ）

A. B. C. D.

10.、两地相距，甲、乙两人沿同一条路从地到地，，分别表示甲、乙两人离开地的距离（）与时间（）之间的关系。以下说法正确的是（    ）

A.乙车出发1.5小时后甲才出发

B.两人相遇时，他们离开地

C.甲的速度是

D.乙的速度是

第Ⅱ卷非选择题（共90分）

二、填空题（每小题3分，共计30分）

11.中国财政部2021年3月18日发布数据显示。前2个月，全国一般公共预算收入约为41800亿元。将41800用科学记数法表示应为______.

12.函数的自变量的取值范围为______.

13.因式分解：______.

14.不等式组的解集是______.

15.已知二次函数，当时，随的增大而增大，则的取值范围是______.

16.如图，在平面直角坐标系中，点是函数（，）图象上的一点，轴于点，的面积为6.若点也在此函数的图象上，则的值为______.

17.已知一个扇形的弧长为，面积为，则此扇形的圆心角是______.

18.在一个不透明的布袋中装有4个白球和个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球，摸到白球的概率是，则______.

19.在三角形中，，为高，两条高所在的直线相交于点，若，则的大小为______.

20.如图，是矩形的对角线，，，点，分别是线段，上的点，连接，.当，且时，______.

三、解答题（其中21-22题各7分，23~24题各8分，25~27题各10分，共计60分）

21.（本题7分）

先化简，再求代数式的值，其中.

22.（本题7分）

如图是由边长为1的小正方形构成的网格（下面所画三角形顶点都在小正方形顶点上）.

（1）在图1中画出以为直角边的等腰直角三角形，并且直接写出线段的长度；

（2）在图2中画出一个以为一腰的等腰三角形，使.

23.（本题8分）

为有效控制新型冠状病毒的传染，目前，国家正全面推开新冠疫苗的免费接种工作。某社区为了解其辖区内居民的接种情况，随机抽查了一部分居民进行问卷调查，把调查的结果分为A（已经接种）、B（准备接种）、C（观望中）、D（不接种）四种类别，并绘制了两幅不完整的统计图，请根据图中提供的信息解答下列问题：

（1）此次抽查的居民人数为______人；

（2）请补全条形统计图，同时求出C类别所在扇形的圆心角度数；

（3）若该社区共有居民4000人，请你估计该社区已接种新冠疫苗的居民约有多少人？

24.（本题8分）

在正方形中，是中点，是上一点，且.

（1）如图1，求证：；

（2）如图2，连接，延长交的延长线于点，过点作交于点，垂足为，交于点，在不添加任何辅助线的情况下，请直接写出图2中的所有等腰三角形.

25.（本题10分）

“你怎么样，中国便是怎么样；你若光明，中国便不黑暗”.2019年，一场新冠肺炎疫情牵扯着人们的心灵，各界人士齐心协力，众志成城.针对资源急需问题，某医疗设备公司紧急复工，但受疫情影响，医用防护服生产车间仍有7人不能到厂生产。为了应对疫情，已复产的工人加班生产，由原来每天工作8小时增加到10小时，每小时完成的工作量不变。原来每天能生产防护服800套，现在每天能生产防护服650套.

（1）求原来生产防护服的工人有多少人；

（2）复工10天后，未到的工人同时到岗加入生产，每天生产时间仍然为10小时.公司决定将复工后生产的防护服14500套捐献给某地，则至少还需要生产多少天才能完成任务？

26.（本题10分）

如图，四边形内接于，为直径，和交于点，.

（1）求的度数；

（2）过作的平行线，交于，试判断线段，，之间满足的等量关系，并说明理由；

（3）在（2）条件下过，分别作，的垂线，垂足分别为，，连接，交于，若，，求的半径.

27.（本题10分）

在平面直角坐标系中，点为坐标原点，抛物线交轴负半轴于点，交轴正半轴于点，交轴于点，.

（1）如图1，求抛物线的解析式；

（2）如图2，点在抛物线上，且点在第二象限，连接交轴于点，若，求点的坐标；

（3）如图3，在（2）的条件下，点在抛物线上，且点在第三象限，点在上，，过点作轴的垂线，点为垂足，连接并延长交于点，若，求的长.

参考答案

1.B   2.B   3.C   4.A   5.B   6.D   7.A   8.D   9.C   10.D

11.   12.   13.   14.   15.   16.3   17.   18.8

19.或

【解析】

20.

【解析】解∶过点作于点，

∴≌（AAS），

∴，

∵，

∴，，

∴，

∵，∴，

∴，

∴，，

∴.

21.解∶原式，

当时，原式.

22.解∶（1）如图，即为所求作，.

（2）如图，即为所求作.

23.解∶（1）200；

（2）类人数∶（人），

补全条形统计图如下∶

类别所在扇形的圆心角度数是∶

（3）（人），

答∶估计该社区已经接种新冠疫苗的居民约有1200人.

24.（1）证明∶∵四边形为正方形，

∴，.

∵是中点，∴，.

∵，∴，∴.

∴∽.∴.

∵，

∴，∴.

（2）解∶等腰三角形有∶，，，.

25.解∶（1）设原来生产防护服的工人有人，

由题意得，，

解得∶.

经检验，是原方程的解.

答∶原来生产防护服的工人有20人；

（2）设还需要生产天才能完成任务.

（套），

即每人每小时生产5套防护服.

由题意得，，

解得.

答∶至少还需要生产8天才能完成任务.

26.解∶（1）∵为直径，∴，

∴，

∵，∴，

∴；

（2）线段，，之间满足的等量关系为∶.理由如下∶

如图2，设，，

∵，∴，

又，∴，

过作，使，连接，

∵，，，

∴≌（SAS），

∴，，

∴.

∵，，，

∴≌（SAS），∴，

∵在中，，

∴；

（3）如图3，延长，交于，

由（2）知，

∴，

∴，

∴，即，

∴，

∴，

∴，，

∵，

∴，

∵平分，∴，

设，，∴，

∵，∴，

∴，，

∵，

∴，

整理得∶，

解得∶（舍去），.

∴，∴，

∴的半径为.

27.解∶（1）∵二次函数，

∴当时，，，∴，

∵，，，

∴，，

∴，解得，

∴抛物线的解析式为；

（2）过点作轴的垂线，点为垂足，设点的横坐标为，则点的纵坐标为，

∵点在第二象限，∴，

∵，，∴，

在中，，

∵，

∴，，解得（舍去），，

∴点的纵坐标为，

∴点的坐标为；

（3）连接，∵，，，

∴≌（SSS），∴；

过点作轴的垂线，点为垂足，

∵，∴，

∵，

∴四边形为矩形；∵，∴四边形为正方形；

取的中点，连接，过点作的垂线交的延长线于点，

在中，，∴；

∵，∴，∴；

∵；

∴，∴≌（SAS），

∴，

∵，∴，

∵，，，

∴；

在中，，，，

∴，∴，

在中，，，

在中，，∴；

在中，，

∴，∵四边形为正方形，

∴设，，，，，

∵，∴，

在中，，

在中，，

∴，

解得（舍去），；

∴.

过点作轴的垂线，垂足为，设点的横坐标为，则点的纵坐标为，

∵点在第三象限，

∴，

在中，，

∴，

∵，∴，

∴，解得（舍去），，

∴，.

在中，，∴