初中数学人教版七年级上册第四章 几何图形初步4.2 直线、射线、线段教课ppt课件

这是一份初中数学人教版七年级上册第四章 几何图形初步4.2 直线、射线、线段教课ppt课件，共18页。PPT课件主要包含了线段长短的比较与运算，线段长短的比较，差倍分，度量法，叠合法，思想方法，方程思想，分类思想，基本作图，知识回顾等内容，欢迎下载使用。

1. 体会文字语言、符号语言和图形语言的相互转化.
2. 了解两点间距离的意义，理解“两点之间，线段最短”的线段性质，并学会运用.
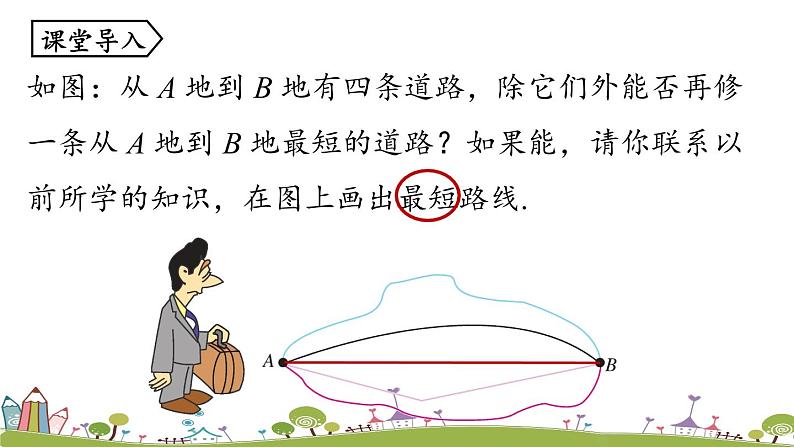
如图：从 A 地到 B 地有四条道路，除它们外能否再修一条从 A 地到 B 地最短的道路？如果能，请你联系以前所学的知识，在图上画出最短路线.
经过比较，我们可以得到一个关于线段的基本事实：
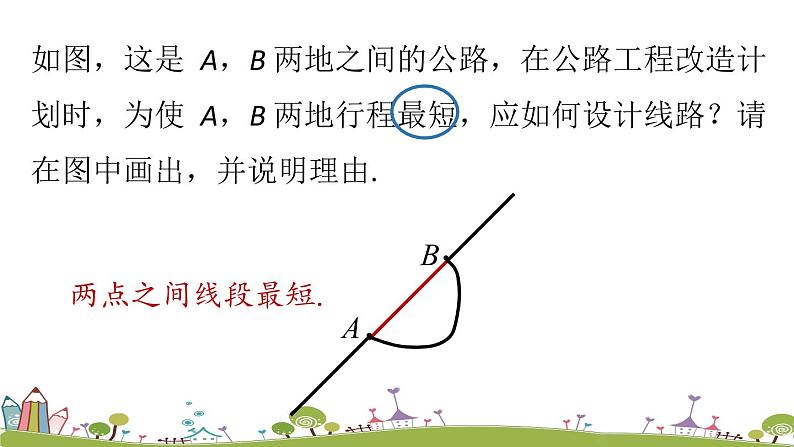
两点的所有连线中，线段最短.
简单说成：两点之间，线段最短.
知识点 关于线段的基本事实及两点的距离
如图，这是 A，B 两地之间的公路，在公路工程改造计划时，为使 A，B 两地行程最短，应如何设计线路？请在图中画出，并说明理由.
由于“两点之间，线段最短”，这样做增加桥的长度，一方面使这座桥能容纳更多的游人来观光，另一方面也增加了游人在桥上行走的路程，有利于游人更好地观赏湖面风光.
如图，公园里修建了曲折迂回的桥，这与修一座直的桥相比，对游人观赏湖面风光能起到什么作用？用你所学数学知识说明其中的道理.
连接两点间的线段的长度，叫做这两点的距离.
例1 如图，已知 A，B，C，D 为四个居民小区，现要建一个购物中心，不考虑其他因素，请你画图确定购物中心 O 的位置，使它到四个居民小区的距离之和最小.
解：如图，连接 AC，BD 相交于点 O，点 O 就是购物中心的位置.
1.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分，发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是 .
解：结合线段的性质，知能正确解释这一现象的数学知识是“两点之间，线段最短”.
2.如图所示，某同学的家在 A 处，星期日他到书店去买书，若想尽快赶到书店 B ，则最近的路线是( )A. A→C→D→BB. A→C→F→BC. A→C→E→F→BD. A→C→M→B
解：根据线段的基本事实，可得 C，B两点之间的最短距离是线段 CB 的长度，所以若想尽快赶到书店，则最近的路线是 A→C→F→B.
3.如图，点 A 和点 B 分别在棱长为20 cm的正方体盒子上相邻的两个面的中心位置，一只虫子由点 A 爬到点 B，则这只虫子爬行的最短路程是 .
解：将正方体盒子中含 A，B 两点的两个面展开，如图所示，连接 AB，由“两点之间，线段最短”可知，虫子沿展开图中的线段 AB 爬行的路线最短. 因为线段 AB 的长度与正方体盒子的棱长相等，所以这只虫子爬行的最短路程为 20 cm.
连接两点间的线段的长度.
1.把一条弯曲的河流改成直道，可以缩短航程，用数学知识解释其道理为( )A．两点确定一条直线B．经过两点有且仅有一条直线C．直线可以向两端无限延伸D．两点之间，线段最短
2.如图,一观测塔底座部分是长方体,现在从下底面 A 点修建钢筋扶梯,经过点 M,N 到点 D' ,再进入顶部的观测室,已知 AB=BC,试确定使扶梯的总长度最小的点 M，N 的位置.
将长方体相应的三个面展开
解:如图, 将长方体的三个面展开,连接 AD, 分别与 BB' , CC' 交于点 M, N,点 M, N 即为所求.
3.在同一个学校上学的小明、小亮、小红三位同学分别住在 A，B，C 三个住宅区，如图所示，A，B，C 三点共线，且 AB=40米，BC=100米，他们打算合租一辆车去上学. 在三个住宅区之间只设一个停靠点，为使三位同学步行到停靠点的路程之和最小，你认为停靠点应该设在何处?