2020-2021学年高一下学期数学人教A版（2019）必修第二册期末模拟测试卷

这是一份2020-2021学年高一下学期数学人教A版（2019）必修第二册期末模拟测试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.给出下列三个结论:①若,则;②若,则;③若,则.其中正确的结论有( )
A.0个B.1个C.2个D.3个
2.设向量，当向量与平行时，( )
A.B.2C.1D.
3.已知复数z满足,则z的共轭复数的虚部为( )
A.B.C.D.
4.若复数，则z的共轭复数为( )
A.B.C.D.
5.某空间几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
6.一个四棱锥的三视图如图所示，则该四棱锥的体积为( )
A． B． C． D．
7.某中学高中部共有80名教师，初中部共有120名教师，其性别比例如图所示，现从中按分层抽样抽取25人进行优质课展示，则应抽取高中部男教师的人数为( )
A.3B.6C.7D.9
8.某产品的广告费用与销售额的统计数据如下表:
根据上表可得回归方程中的为,据此模型预报广告费用为万元时销售额为( )
A. 万元B. 万元C. 万元D. 万元
9.袋中装有红色、黑色、粉色共6个除颜色外其他均相同的小球，其中红色球比黑色球多一个，粉色球个数不超过一个且三种颜色的球都有，现从袋中一次取出3个球，则3个小球颜色各不相同的概率是( )
A.B.C.D.
10.某商场为吸引客流量，凭借满99元的购物小票，可以兑换五个奥运福娃“贝贝”“晶晶”“欢欢”“迎迎”“妮妮”中的任意两个，则两个福娃中含有“贝贝”的概率是( )
A.B.C.D.
11.一盒中有12个乒乓球，其中9个新球，3个旧球，从盒中任取3个球来用，用完后放回盒中，此时盒中旧球个数X是一个随机变量，则( )
A.B.C.D.
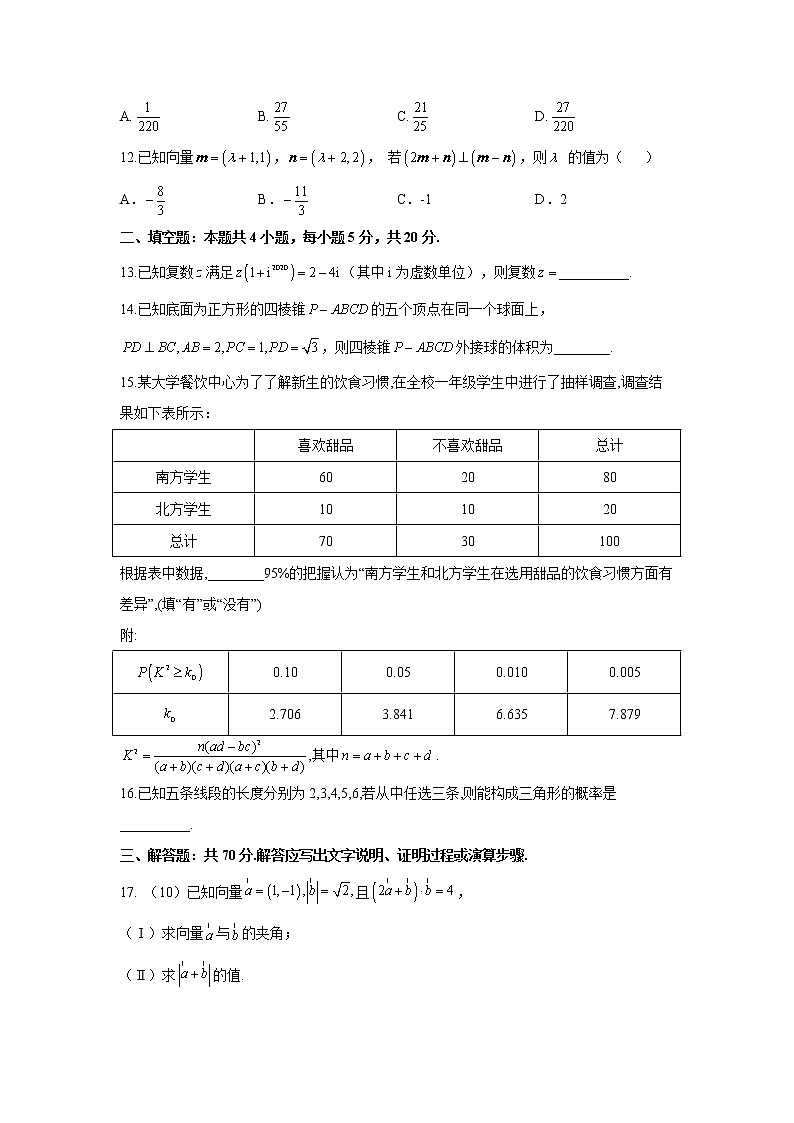
12.已知向量，， 若，则的值为（ ）
A． B． C．-1 D．2
二、填空题：本题共4小题，每小题5分，共20分.
13.已知复数z满足（其中i为虚数单位），则复数__________.
14.已知底面为正方形的四棱锥的五个顶点在同一个球面上，，则四棱锥外接球的体积为________.
15.某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示：
根据表中数据,________95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”,(填“有”或“没有”)
附:
,其中.
16.已知五条线段的长度分别为2,3,4,5,6,若从中任选三条,则能构成三角形的概率是__________.
三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.
17. （10）已知向量且，
（Ⅰ）求向量与的夹角；
（Ⅱ）求的值.
18. （12分）已知复数是纯虚数,i是虚数单位.
(1)求复数z的共轭复数;
(2)若复数所表示的点在第二象限,求实数m的取值范围.
19. （12分）如图，在四棱锥中，平面，，，．
(1)求证：；
(2)当几何体的体积等于时，求四棱锥 的侧面积．
20. （12分）某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表。
(1)分别估计这类企业中产值增长率不低于的企业比例、产值负增长的企业比例；
(2)求这类企业产值增长率的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表）。（精确到）附：.
21. （12分）某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组：第一组,,第二组,,第八组,,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图；
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值)；
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.
22. （12分）如图,矩形ABCD所在平面与所在平面垂直,M是上异于C,D的点.
(1)证明:平面平面BMC.
(2)在线段AM上是否存在点P,使得平面PBD?说明理由
答案以及解析
一、选择题
1.答案：A
解析：①忽略了0与0的区别，；②混淆了两个向量的模相等和两个实数相等，两个向量的模相等只能说明它们的长度相等，它们的方向并不确定；③两个非零向量平行，可以得出它们的方向相同或相反，未必得到它们的模相等.
2.答案：A
解析：与平行，.
.
3.答案：D
解析：依题意,复数，所以z的共轭复数的虚部为，故选D.
4.答案：C
解析：，.
5.答案：C
解析：本题考查由三视图还原几何体、几何体的体积.根据题中三视图可以看出原几何体为一个四棱锥割去半个圆锥，故其体积为.故选C.
6.答案：A
解析：由三视图知，该几何体是一个直四棱锥，底面是一个直角梯形，底面积为，高为2，因此，这个四棱锥的体积为
7.答案：B
解析：高中部的男教师人数为，所以应抽取高中部男教师的人数为.
8.答案：B
解析：由表可计算，
，
∵点在回归直线上，且为，
所以，
解得，
故回归方程为，
令，得。
9.答案：B
解析：设黑色球有x个，则红色球有.个由题意可知，粉色球有1个，则，解得，所以共有3个红色球，2个黑色球，1个粉色球.令1,2,3分别表示三个红色球，a,b表示两个黑色球，
0表示粉色球，则从袋中一次取出3个小球有123，
12a，12b，120,13a，13b，130,1a0,1ab，1b0,23a，23b，
230,2ab，2a0,2b0,3ab，3a0,3b0，ab0，共20种情况，其中颜色各不相同的有1a0,1b0,2a0,2b0,3a0,3b0，共6种情况，记“3个小球颜色各不相同”为事件A，则，故选B.
10.答案：C
解析：从五个福娃中任选两个的情况有（贝贝，晶晶），（贝贝，欢欢），（贝贝，迎迎），（贝贝，妮妮），（晶晶，欢欢），（晶晶，迎迎），（晶晶，妮妮），（欢欢，迎迎），
（欢欢，妮妮），（迎迎，妮妮），共10种，其中含有“贝贝”
的情况有（贝贝，晶晶），（贝贝，欢欢），（贝贝，迎迎），
（贝贝，妮妮），共4种，则两个福娃中含有“贝贝”的概率,故选C.
11.答案：D
解析：因为从盒中任取3个球来用，用完后放回盒中，此时盒中旧球个数为，即旧球增加1个，所以取出的三个球为1个新球，2个旧球，所以，故选D.
12.答案：A
解析：因为，且，
所以，解得.
二、填空题
13.答案：
解析：因为，所以.
14.答案：.
解析：由题意知，所以平面，而平面，则平面平面.由条件知，所以.如图，取的中点G连
接，交于点O，则O为正方形的中心，过点G作平面的垂线，则点O在该垂线上，所以O为四棱锥外接球的球心，由于，所以四棱锥外接球的体积为.
15.答案：有
解析：根据表中数据,计算观测值.对照临界值知,有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异.
16.答案：0.7
解析：基本事件为(2,3,4),(2,3,5),(2,3,6),(2,4,5),(2,4,6),(2,5,6),(3,4,5),(3,4,6),(3,5,6),(4,5,6),共10 种,其中能构成三角形的有(2,3,4),(2,4,5),(2,5,6),(3,4,5),(3,4,6),(3,5,6),(4,5,6),共7种情况,故所求事件的概率0.7.
三、解答题
17.答案：（Ⅰ）由得 因
向量与的夹角为
（Ⅱ）
18.答案：（1）∵，
∴．
又∵是纯虚数，∴，∴，即．
所以
（2）∵，，∴，
又∵复数所表示的点在第二象限，∴解得，
即时，复数所表示的点在第二象限．
19.答案：
(1)解：取的中点F，连结，
则直角梯形中，，
即：
平面，平面

又
(2)解：

，，
又
四棱锥的侧面积为

20.答案：(1)根据产值增长率频数分布表得，所调查的100个企业中产值增长率不低于的企业频率为。
产值负增长的企业频率为。
用样本频率分布估计总体分布得这类企业中产值增长率不低于的企业比例为，产值负增长的企业比例为。
(2)，，。所以，这类企业产值增长率的平均数与标准差的估计值分别为。
21.答案：(1)由频率分布直方图得第七组的频率为：
.
完成频率分布直方图如下：
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分为：
(3)样本成绩属于第六组的有人,样本成绩属于第八组的有人,
从样本成绩属于第六组和第八组的所有学生中随机抽取2名,
基本事件总数,
他们的分差的绝对值小于10分包含的基本事件个数,
他们的分差的绝对值小于10分的概率.
22.答案：（1）由题设知，平面平面ABCD，交线为CD.
因为,平面ABCD,
所以平面CMD.
又平面CMD，故.
因为M为异于C,D的点，且DC为直径，所以.
又，所以平面BMC.
又平面AMD，所以平面平面BMC.
（2）当P为AM的中点时，平面PBD.
证明如下：连接AC,BD并交于点O.因为四边形ABCD为矩形，所以O为AC的中点.
因为P为AM的中点，
所以.
又因为平面PBD,平面PBD,
所以平面PBD.
广告费用 (万元)
4
2
3
5
销售额 (万元)
49
26
39
54
喜欢甜品
不喜欢甜品
总计
南方学生
60
20
80
北方学生
10
10
20
总计
70
30
100
0.10
0.05
0.010
0.005
2.706
3.841
6.635
7.879
y的分组
企业数
2
24
53
14
7