高考数学一轮复习第五章 5.3

这是一份高考数学一轮复习第五章 5.3，共17页。试卷主要包含了向量的夹角，平面向量的数量积，向量数量积的运算律，平面向量数量积的有关结论等内容，欢迎下载使用。

§5.3　平面向量的数量积


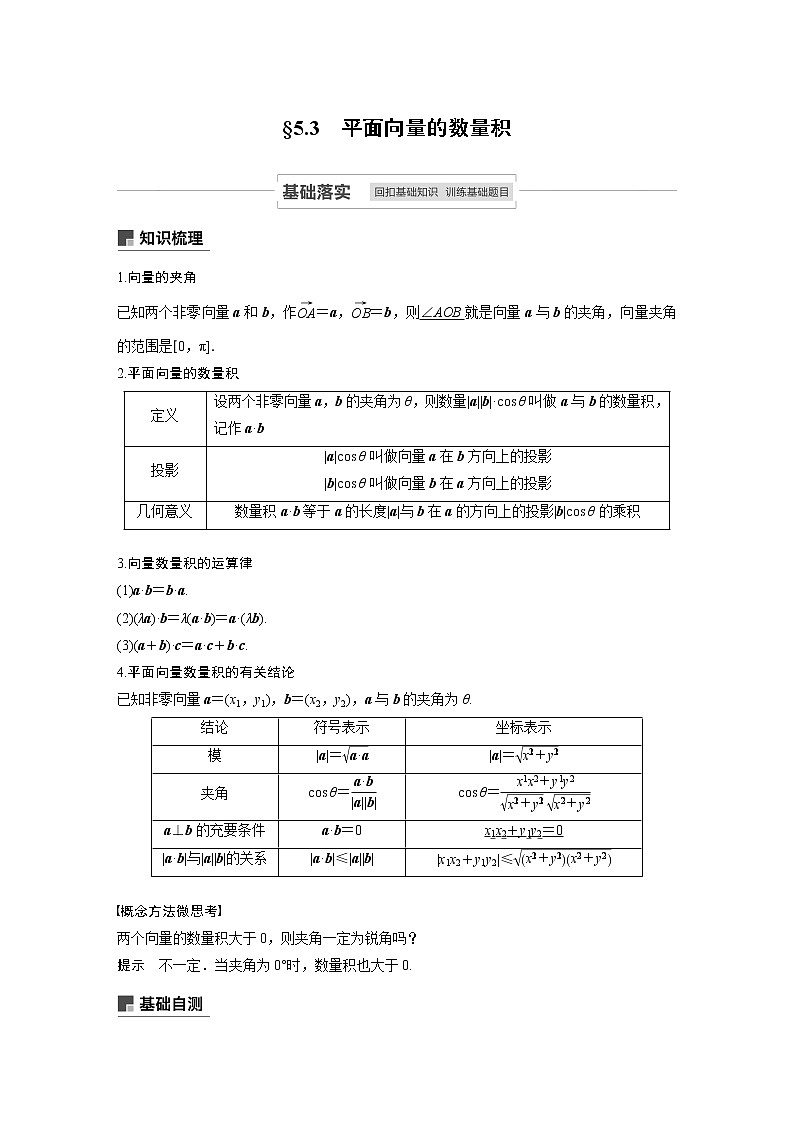
1.向量的夹角
已知两个非零向量a和b，作＝a，＝b，则∠AOB就是向量a与b的夹角，向量夹角的范围是[0，π].
2.平面向量的数量积
定义
设两个非零向量a，b的夹角为θ，则数量|a||b|·cos θ叫做a与b的数量积，记作a·b
投影
|a|cos θ叫做向量a在b方向上的投影
|b|cos θ叫做向量b在a方向上的投影
几何意义
数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cos θ的乘积

3.向量数量积的运算律
(1)a·b＝b·a.
(2)(λa)·b＝λ(a·b)＝a·(λb).
(3)(a＋b)·c＝a·c＋b·c.
4.平面向量数量积的有关结论
已知非零向量a＝(x1，y1)，b＝(x2，y2)，a与b的夹角为θ.
结论
符号表示
坐标表示
模
|a|＝
|a|＝
夹角
cos θ＝
cos θ＝
a⊥b的充要条件
a·b＝0
x1x2＋y1y2＝0
|a·b|与|a||b|的关系
|a·b|≤|a||b|
|x1x2＋y1y2|≤

概念方法微思考
两个向量的数量积大于0，则夹角一定为锐角吗？
提示　不一定．当夹角为0°时，数量积也大于0.

题组一　思考辨析
1．判断下列结论是否正确(请在括号中打“√”或“×”)
(1)两个向量的夹角的范围是.(　×　)
(2)由a·b＝0可得a＝0或b＝0.(　×　)
(3)(a·b)c＝a(b·c)．(　×　)
(4)若a·b<0，则a和b的夹角为钝角．(　×　)
题组二　教材改编
2．已知向量a＝(2,1)，b＝(－1，k)，a·(2a－b)＝0，则k＝________.
答案　12
解析　∵2a－b＝(4,2)－(－1，k)＝(5,2－k)，
由a·(2a－b)＝0，得(2,1)·(5,2－k)＝0，
∴10＋2－k＝0，解得k＝12.
3．已知|a|＝2，|b|＝6，a·b＝－6，则a与b的夹角θ＝________.
答案　
解析　cos θ＝＝＝－，
又因为0≤θ≤π，所以θ＝.
题组三　易错自纠
4．已知a，b为非零向量，则“a·b>0”是“a与b的夹角为锐角”的(　　)
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
答案　B
解析　根据向量数量积的定义可知，若a·b>0，则a与b的夹角为锐角或零角，若a与b的夹角为锐角，则一定有a·b>0，所以“a·b>0”是“a与b的夹角为锐角”的必要不充分条件，故选B.
5．已知矩形ABCD中，||＝6，||＝4，若点M，N满足＝3，＝2，则·等于(　　)
A．20 B．15 C．9 D．6
答案　C
解析　因为ABCD为矩形，建系如图．A(0,0)，M(6,3)，N(4,4)．

则＝(6,3)，＝(2，－1)，
·＝6×2－3×1＝9.
6．(多选)在△ABC中，＝c，＝a，＝b，在下列命题中，是真命题的为(　　)
A．若a·b>0，则△ABC为锐角三角形
B．若a·b＝0，则△ABC为直角三角形
C．若a·b＝c·b，则△ABC为等腰三角形
D．若(a＋c－b)·(a＋b－c)＝0，则△ABC为直角三角形
答案　BCD
解析　①若a·b>0，则∠BCA是钝角，△ABC是钝角三角形，A错误；②若a·b＝0，则⊥，△ABC为直角三角形，B正确；③若a·b＝c·b，b·(a－c)＝0，·(－)＝0，·(＋)＝0，取AC的中点D，则·＝0，所以BA＝BC，即△ABC为等腰三角形，C正确；④若(a＋c－b)·(a＋b－c)＝0，则a2＝(c－b)2，即b2＋c2－a2＝2b·c，即＝－cos A，由余弦定理可得cos A＝－cos A，即cos A＝0，即A＝，即△ABC为直角三角形，D正确，综上真命题为BCD.
7．已知向量a，b的夹角为60°，|a|＝2，|b|＝1，则|a＋2b|＝________.
答案　2
解析　方法一　|a＋2b|＝
＝
＝
＝＝2.
方法二　(数形结合法)
由|a|＝|2b|＝2知，以a与2b为邻边可作出边长为2的菱形OACB，如图，则|a＋2b|＝||.

又∠AOB＝60°，所以|a＋2b|＝2.
平面向量数量积的基本运算
例1　如图，在梯形ABCD中，AB∥CD，CD＝2，∠BAD＝，若·＝2·，则·＝________.

答案　12
解析　方法一　(几何法)
因为·＝2·，
所以·－·＝·，
所以·＝·，
因为AB∥CD，CD＝2，∠BAD＝，
所以2||＝||·||cos ，
化简得||＝2.
故·＝·(＋)＝||2＋·
＝(2)2＋2×2cos ＝12.
方法二　(坐标法)如图，建立平面直角坐标系xAy.

依题意，可设点D(m，m)，C(m＋2，m)，B(n,0)，其中m>0，n>0，
则由·＝2·，
得(n,0)·(m＋2，m)＝2(n,0)·(m，m)，
所以n(m＋2)＝2nm，化简得m＝2.
故·＝(m，m)·(m＋2，m)＝2m2＋2m＝12.
思维升华　平面向量数量积的三种运算方法
(1)当已知向量的模和夹角时，可利用定义法求解，即a·b＝|a||b|cos〈a，b〉．
(2)当已知向量的坐标时，可利用坐标法求解，即若a＝(x1，y1)，b＝(x2，y2)，则a·b＝x1x2＋y1y2.
(3)利用数量积的几何意义求解．
跟踪训练1　(1)在正三角形ABC中，D是BC上的点，若AB＝3，BD＝1，则·＝________.
答案　
解析　如图所示，·＝·(＋)＝9＋3×cos 120°＝.

(2)已知梯形ABCD中，AB∥CD，AB＝2CD，且∠DAB＝90°，AB＝2，AD＝1，若点Q满足＝2，则·等于(　　)
A．－ B. C．－ D.
答案　D
解析　以A为坐标原点，AB所在直线为x轴，AD所在直线为y轴，建立平面直角坐标系，如图所示，

则B(2,0)，C(1,1)，D(0,1)，
又＝2，∴Q，
∴＝，＝，
∴·＝＋1＝.故选D.
平面向量数量积的应用
命题点1　求向量的模
例2　(1)(2020·遵义统考)已知两个单位向量a和b的夹角为120°，k∈R，则|ka＋b|的最小值为(　　)
A. B. C．1 D.
答案　B
解析　|ka＋b|2＝k2a2＋2ka·b＋b2
因为a和b是单位向量，且夹角为120°，
所以|ka＋b|2＝k2a2＋2ka·b＋b2
＝k2|a|2＋2k|a||b|cos〈a，b〉＋|b|2
＝k2－k＋1
＝2＋≥，
所以|ka＋b|≥，
所以|ka＋b|的最小值为.
(2)(2020·四川双流中学诊断)如图，在△ABC中，M为BC的中点，若AB＝1，AC＝3，与的夹角为60°，则||＝________.

答案　
解析　∵M为BC的中点，
∴＝(＋)，
∴||2＝(＋)2
＝(||2＋||2＋2·)
＝(1＋9＋2×1×3cos 60°)＝，
∴||＝.
命题点2　求向量的夹角
例3　(1)(2020·昆明一中检测)已知向量a＝，|b|＝2，且a·b＝1，则a与b的夹角为(　　)
A．30° B．45° C．60° D．90°
答案　C
解析　|a|＝＝1，
∴cos〈a，b〉＝＝，
∴a与b的夹角为60°.
(2)已知e1，e2是互相垂直的单位向量．若e1－e2与e1＋λe2的夹角为60°，则实数λ的值是________．
答案　
解析　由题意知|e1|＝|e2|＝1，e1·e2＝0，
|e1－e2|＝
＝
＝＝2.
同理|e1＋λe2|＝.
所以cos 60°＝
＝
＝＝，
解得λ＝.
思维升华　(1)求解平面向量模的方法
①利用公式|a|＝.
②利用|a|＝.
(2)求平面向量的夹角的方法
①定义法：cos θ＝，θ的取值范围为[0，π]．
②坐标法：若a＝(x1，y1)，b＝(x2，y2)，则cos θ＝.
③解三角形法：把两向量的夹角放到三角形中．
跟踪训练2　(1)(2019·江西省临川一中模拟)已知向量a＝(3,4)，b＝(－1，k)，且a⊥b，则a＋4b与a的夹角为________．
答案　
解析　因为a⊥b，故a·b＝0，所以－3＋4k＝0，
故k＝，故a＋4b＝(－1,7)，
设a＋4b与a的夹角为θ，
则cos θ＝＝＝，
因θ∈[0，π]，故θ＝.
(2)(2019·日照模拟) 已知向量a，b，c满足|a|＝4，|b|＝2，〈a，b〉＝，(c－a)·(c－b)＝
－1，则|c－a|的最大值为________．
答案　＋1
解析　设＝a，＝b，＝c，以OA所在的直线为x轴，O为坐标原点建立平面直角坐标系(图略)，
∵|a|＝4，|b|＝2，a与b的夹角为，
则A(4,0)，B(2,2)，设C(x，y)，
∵(c－a)·(c－b)＝－1，∴x2＋y2－6x－2y＋9＝0，
即(x－3)2＋(y－1)2＝1，∴点C在以(3,1)为圆心，1为半径的圆上，|c－a|表示点A，C的距离，即圆上的点与A(4,0)的距离，∵圆心到A的距离为，
∴|c－a|的最大值为＋1.
平面向量与三角函数、解三角形
例4　(2019·石家庄模拟)已知向量a＝(sin x，cos x)，b＝(cos x，cos x)，f (x)＝a·b.
(1)求函数f (x)＝a·b的最小正周期；
(2)在△ABC中，BC＝，sin B＝3sin C，若f (A)＝1，求△ABC的周长．
解　(1)f (x)＝sin xcos x＋cos2x
＝sin 2x＋cos 2x＋，
f (x)＝sin＋，
所以f (x)的最小正周期T＝＝π.
(2)由题意可得sin＝，
又0 所以2A＋＝，故A＝.
设角A，B，C的对边分别为a，b，c，则a2＝b2＋c2－2bccos A.
所以a2＝b2＋c2－bc＝7，
又sin B＝3sin C，所以b＝3c.
故7＝9c2＋c2－3c2，解得c＝1.
所以b＝3，△ABC的周长为4＋.
思维升华　平面向量与三角函数的综合问题的解题思路
(1)题目条件给出向量的坐标中含有三角函数的形式，运用向量共线或垂直或等式成立等，得到三角函数的关系式，然后求解．
(2)给出用三角函数表示的向量坐标，要求的是向量的模或者其他向量的表达形式，解题思路是经过向量的运算，利用三角函数在定义域内的有界性，求得值域等．
跟踪训练3　在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，已知向量m＝，n＝(c，b－2a)，且m·n＝0.
(1)求∠C的大小；
(2)若点D为边AB上一点，且满足＝，||＝，c＝2，求△ABC的面积．
解　(1)因为m＝(cos B，cos C)，n＝(c，b－2a)，m·n＝0，
所以ccos B＋(b－2a)cos C＝0，
在△ABC中，由正弦定理得，
sin Ccos B＋(sin B－2sin A)cos C＝0，
sin A＝2sin Acos C，
又sin A≠0，
所以cos C＝，而C∈(0，π)，所以∠C＝.
(2)由＝知，－＝－，
所以2＝＋，
两边平方得4||2＝b2＋a2＋2bacos∠ACB＝b2＋a2＋ba＝28.①
又c2＝a2＋b2－2abcos∠ACB，
所以a2＋b2－ab＝12.②
由①②得ab＝8，
所以S△ABC＝absin∠ACB＝2.

1．(2019·江西省临川第一中学模拟)已知向量a＝(2,1)，b＝(m，－1)，且a⊥(a－b)，则m的值为(　　)
A．1 B．3 C．1或3 D．4
答案　B
解析　因为a＝(2,1)，b＝(m，－1)，
所以a－b＝(2－m,2)，
因为a⊥(a－b)，则a·(a－b)＝2(2－m)＋2＝0，
解得m＝3.故选B.
2．(2019·全国Ⅱ)已知＝(2,3)，＝(3，t)，||＝1，则·等于(　　)
A．－3 B．－2 C．2 D．3
答案　C
解析　因为＝－＝(1，t－3)，所以||＝＝1，解得t＝3，所以＝(1,0)，所以·＝2×1＋3×0＝2，故选C.
3．(2020·拉萨模拟)已知向量a，b的夹角为，且a＝(2，－1)，|b|＝2，则|a＋2b|等于(　　)
A．2 B．3 C. D.
答案　C
解析　由已知|a|＝＝，
a·b＝|a||b|cos ＝0，
∴|a＋2b|2＝(a＋2b)2＝a2＋4a·b＋4b2
＝()2＋4×22＝21，
∴|a＋2b|＝.故选C.
4．(2019·湖南省桃江县第一中学模拟)已知向量a，b满足|a|＝，|b|＝1，且|b＋a|＝2，则向量a与b的夹角的余弦值为(　　)
A. B. C. D.
答案　D
解析　由题意可知，|b＋a|2＝b2＋2a·b＋a2＝3＋2a·b＝4，解得a·b＝，∴cos〈a，b〉＝＝＝，故选D.
5．(2019·东莞模拟)已知非零向量m，n满足|n|＝4|m|，且m⊥(2m＋n)，则m，n的夹角为(　　)
A. B. C. D.
答案　D
解析　∵|n|＝4|m|，且m⊥(2m＋n)，
∴m·(2m＋n)＝2m2＋m·n＝2|m|2＋|m||n|cos〈m，n〉＝0，
且|m|≠0，|n|≠0，
∴2|m|＋|n|cos〈m，n〉＝0，
∴cos〈m，n〉＝－＝－，
又0≤〈m，n〉≤π，∴〈m，n〉＝.故选D.
6．已知向量a＝(sin θ，)，b＝(1，cos θ)，|θ|≤，则|a－b|的最大值为(　　)
A．2 B. C．3 D．5
答案　B
解析　由已知可得|a－b|2＝(sin θ－1)2＋(－cos θ)2＝5－4sin.因为|θ|≤，所以0≤θ＋≤，所以当θ＝－时，|a－b|2的最大值为5－0＝5，
故|a－b|的最大值为.
7．(多选)设a，b是两个非零向量．则下列命题为假命题的是(　　 )
A．若|a＋b|＝|a|－|b|，则a⊥b
B．若a⊥b，则|a＋b|＝|a|－|b|
C．若|a＋b|＝|a|－|b|，则存在实数λ，使得b＝λa
D．若存在实数λ，使得b＝λa，则|a＋b|＝|a|－|b|
答案　ABD
解析　对于A，若|a＋b|＝|a|－|b|，
则|a|2＋|b|2＋2a·b＝|a|2＋|b|2－2|a||b|，
得a·b＝－|a||b|≠0，a与b不垂直，所以A为假命题；
对于B，由A解析可知，若a⊥b，则|a＋b|≠|a|－|b|，所以B为假命题；
对于C，若|a＋b|＝|a|－|b|，
则|a|2＋|b|2＋2a·b＝|a|2＋|b|2－2|a||b|，
得a·b＝－|a||b|，则cos θ＝－1，
则a与b反向，因此存在实数λ，使得b＝λa，所以C为真命题．
对于D，若存在实数λ，使得b＝λa，
则a·b＝λ|a|2，－|a||b|＝λ|a|2，由于λ不能等于0，
因此a·b≠－|a||b|，则|a＋b|≠|a|－|b|，
所以D不正确．
故选ABD.
8．(多选)设a，b，c是任意的非零平面向量，且相互不共线，则下列命题中的真命题是(　　 )
A．(a·b)c－(c·a)b＝0
B．|a|－|b|＜|a－b|
C．(b·c)a－(a·c)b不与c垂直
D．(3a＋2b)·(3a－2b)＝9|a|2－4|b|2
答案　BD
解析　由于b，c是不共线的向量，因此(a·b)c与(c·a)b相减的结果应为向量，故A错误；
由于a，b不共线，故a，b，a－b构成三角形，因此B正确；
由于[(b·c)a－(c·a)b]·c＝(b·c)(a·c)－(c·a)(b·c)＝0，故C中两向量垂直，故C错误；
根据向量数量积的运算可以得出D是正确的．
故选BD.
9．(2020·景德镇模拟)已知两个单位向量a，b的夹角为30°，c＝ma＋(1－m)b，b·c＝0，则m＝________.
答案　4＋2
解析　b·c＝b·[ma＋(1－m)b]＝ma·b＋(1－m)b2
＝m|a||b|cos 30°＋(1－m)|b|2＝m＋1－m＝0，
所以m＝4＋2.
10．(2019·天津模拟)已知菱形ABCD的边长为2，∠ABC＝60°，点E，F分别在边AD，DC上，＝(＋)，＝，则·＝________.
答案　
解析　连接AC，BD交于点O，以O为原点，以，的方向分别为x轴、y轴的正方向建立直角坐标系，如图所示，

∵菱形边长为2，∠ABC＝60°，
∴A(－1,0)，B(0，－)，C(1,0)，D(0，)，
∵＝(＋)，
∴E为AD的中点，∴E，
∵＝，∴F，
∴＝，＝，
∴·＝－＋＝.
11．已知|a|＝4，|b|＝3，(2a－3b)·(2a＋b)＝61.
(1)求a与b的夹角θ；
(2)求|a＋b|；
(3)若＝a，＝b，求△ABC的面积．
解　(1)因为(2a－3b)·(2a＋b)＝61，
所以4|a|2－4a·b－3|b|2＝61.
又|a|＝4，|b|＝3，所以64－4a·b－27＝61，
所以a·b＝－6，所以cos θ＝＝＝－.
又0≤θ≤π，所以θ＝.
(2)|a＋b|2＝(a＋b)2＝|a|2＋2a·b＋|b|2
＝42＋2×(－6)＋32＝13，
所以|a＋b|＝.
(3)因为与的夹角θ＝，
所以∠ABC＝π－＝.
又||＝|a|＝4，||＝|b|＝3，
所以S△ABC＝||||·sin∠ABC
＝×4×3×＝3.
12．已知向量a＝(cos x，sin x)，b＝(3，－)，x∈[0，π]．
(1)若a∥b，求x的值；
(2)记f (x)＝a·b，求f (x)的最大值和最小值以及对应的x的值．
解　(1)因为a＝(cos x，sin x)，b＝(3，－)，a∥b，所以－cos x＝3sin x.
若cos x＝0，则sin x＝0，与sin2x＋cos2x＝1矛盾，
故cos x≠0，于是tan x＝－.
又x∈[0，π]，所以x＝.
(2)f (x)＝a·b＝(cos x，sin x)·(3，－)
＝3cos x－sin x＝2cos.
因为x∈[0，π]，所以x＋∈，
从而－1≤cos≤.
于是，当x＋＝，即x＝0时，f (x)取得最大值3；
当x＋＝π，即x＝时，f (x)取得最小值－2.

13．(2019·衡阳模拟)在△ABC中，∠A＝120°，·＝－3，点G是△ABC的重心，则||的最小值是(　　)
A. B. C. D.
答案　B
解析　设BC的中点为D，
因为点G是△ABC的重心，
所以＝＝×(＋)＝(＋)，
再令||＝c，||＝b，
则·＝bccos 120°＝－3，所以bc＝6，
所以||2＝(||2＋2·＋||2)
＝(c2＋b2－6)≥(2bc－6)＝，
所以||≥，
当且仅当b＝c＝时取等号，故选B.
14．(多选)如图所示，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝2，CD＝1，BC＝a(a＞0)，P为线段AD(含端点)上一个动点，设＝x，·＝y，对于函数y＝f (x)，以下四个结论中正确的是(　　 )

A．当a＝2时，函数的值域为[1,4]
B．∀a∈(0，＋∞)，都有f (1)＝1成立
C．∀a∈(0，＋∞)，函数f (x)的最大值都等于4
D．若f (x)在(0,1)上单调递减，则a∈(0，]
答案　BCD
解析　如图所示，建立直角坐标系．

∵在直角梯形ABCD中，AB∥CD，AB⊥BC，AB＝2，CD＝1，BC＝a(a＞0)，
∴B(0,0)，A(－2,0)，D(－1，a)，C(0，a)．
∵＝x(0≤x≤1)．
∴＝＋＝(－2,0)＋x(1，a)＝(x－2，xa)，
＝＋＝－(x－2，xa)＋(0，a)＝(2－x，a－xa)．
∴y＝f (x)＝·＝(2－x，－xa)·(2－x，a－xa)
＝(2－x)2－ax(a－xa)
＝(a2＋1)x2－(4＋a2)x＋4(0≤x≤1)．
当a＝2时，y＝f (x)＝5x2－8x＋4＝52＋，
∵0≤x≤1，∴当x＝时，f (x)取得最小值；
又f (0)＝4，f (1)＝1，∴f (x)max＝f (0)＝4.
综上可得，函数f (x)的值域为，因此A不正确．
由y＝f (x)＝(a2＋1)x2－(4＋a2)x＋4.
可得∀a∈(0，＋∞)，都有f (1)＝1成立，因此B正确；
由y＝f (x)＝(a2＋1)x2－(4＋a2)x＋4.
可知对称轴x0＝.
当0＜a≤时，x0≥1，
∴函数f (x)在[0,1]上单调递减，
因此当x＝0时，函数f (x)取得最大值4.当a＞时，0＜x0＜1，函数f (x)在[0，x0)上单调递减，在(x0，1]上单调递增．
又f (0)＝4，f (1)＝1，
∴f (x)max＝f (0)＝4.因此C正确．
f (x)在(0,1)上单调递减，
则a∈(0，]，因此D正确．
故选BCD.


15．若向量a，b，c满足a≠b，c≠0，且(c－a)·(c－b)＝0，则的最小值是(　　)
A. B．2 C．2 D.
答案　C
解析　设向量a＝，b＝，c＝，
则由(c－a)·(c－b)＝0得·＝0，
即C的轨迹为以AB为直径的圆，圆心为AB的中点M，半径为||，
因此|c|＝||≤||＋r＝|＋|＋||
＝|＋|＋|－|
＝|a＋b|＋|a－b|，
从而≥2，故选C.
16.在如图所示的平面直角坐标系中，已知点A(1,0)和点B(－1,0)，||＝1，且∠AOC＝θ，其中O为坐标原点．

(1)若θ＝，设点D为线段OA上的动点，求|＋|的最小值；
(2)若θ∈，向量m＝，n＝(1－cos θ，sin θ－2cos θ)，求m·n的最小值及对应的θ值．
解　(1)设D(t,0)(0≤t≤1)，
由题意知C，
所以＋＝，
所以|＋|2＝2＋，
所以当t＝时，|＋|最小，最小值为.
(2)由题意得C(cos θ，sin θ)，m＝＝(cos θ＋1，sin θ)，
则m·n＝1－cos2θ＋sin2θ－2sin θcos θ
＝1－cos 2θ－sin 2θ＝1－sin，
因为θ∈，所以≤2θ＋≤，
所以当2θ＋＝，即θ＝时，sin取得最大值1，即m·n取得最小值1－.
所以m·n的最小值为1－，此时θ＝.