初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定教学演示课件ppt

这是一份初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定教学演示课件ppt，共29页。PPT课件主要包含了相似三角形的判定定理，知识点1，判定定理1，∵DE∥BC，判定定理2，两个判定定理，且∠A∠C，且∠B∠B，运用判定定理1和2，知识点2等内容，欢迎下载使用。

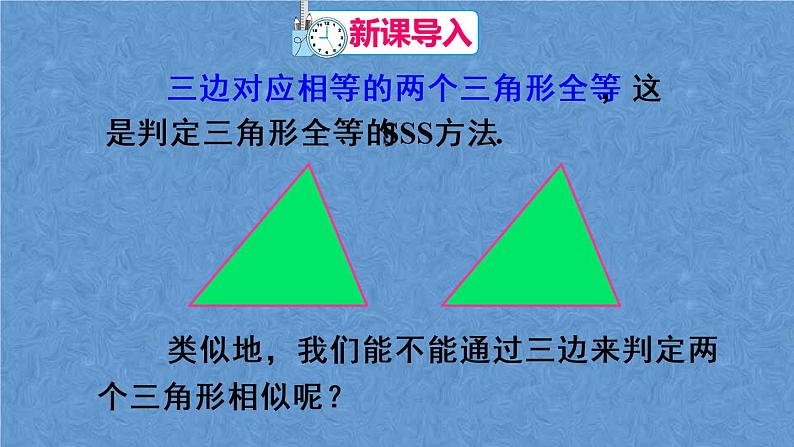
三边对应相等的两个三角形全等，这是判定三角形全等的SSS方法.
类似地，我们能不能通过三边来判定两个三角形相似呢？
学习目标： 1.知道三边成比例的两个三角形相似，知道两边成比例且夹角相等的两个三角形相似. 2.能够运用这两个判定定理解决简单的证明和计算问题.
任意画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的k倍. 度量这两个三角形的角，他们分别相等吗？这两个三角形相似吗？与同学交流一下，看看是否有同样的结论.
通过测量结果，可以发现，这两个三角形相似. 我们用上面的定理进行证明.
如图，在△ABC和△A'B'C'中，求证△ABC∽△A'B'C'
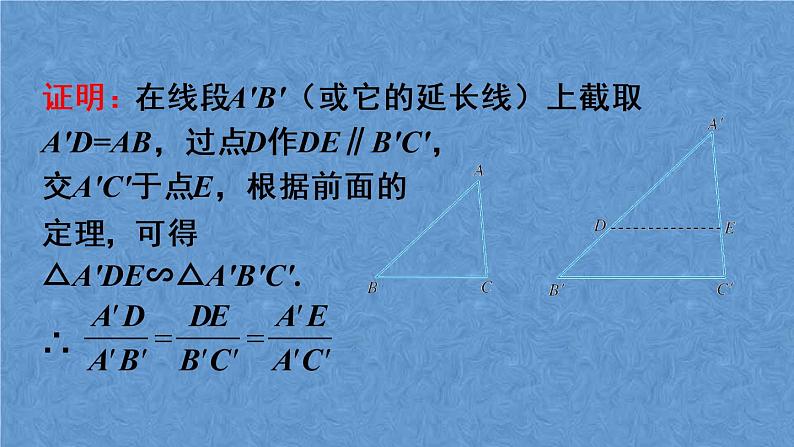
证明：在线段A'B'（或它的延长线）上截取A'D=AB，过点D作DE∥B'C'，交A'C'于点E，根据前面的定理，可得△A'DE∽△A'B'C'.∴
又 ，A'D=AB
∴ ,
∴DE=BC，A'E=AC
∴△A'DE≌△ABC
∴△ABC∽△A'B'C'
△ A'DE是证明的中介，它把△ABC与△A'B'C'联系起来.
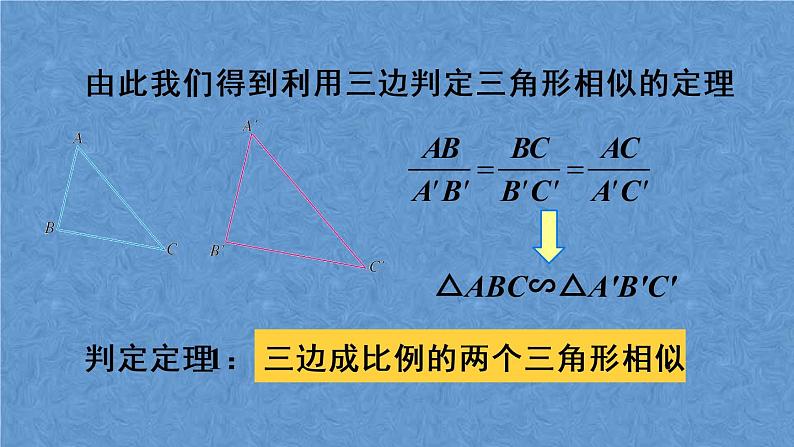
由此我们得到利用三边判定三角形相似的定理
△ABC∽△A'B'C'
三边成比例的两个三角形相似.
全等三角形还可以用SAS来判定，那么相似三角形呢？能不能通过两边和夹角来判定两个三角形相似呢？
证明：在A'B'上截取A'D=AB，作DE∥B'C'交A'C'于点E.
∴△A'DE∽△A'B'C'
由此我们得到另一个判定三角形相似的定理
两边成比例且夹角相等的两个三角形相似.
1.下列条件能判定△ABC与△A′B′C′相似的是（ ）
A. B. C. D.
2.下列四个选项中的三角形，与图中的三角形相似的是（ ）
A. B. C. D.
对于△ABC和△A'B'C'，如果 ∠B=∠B'，这两个三角形一定相似吗？试着画画看？
有两种情况，所以以上条件下，△ABC和△A'B'C'不一定相似.
若把∠B换成∠C，情况一样。
例1 根据下列条件，判断△ABC与△A'B'C'是否相似，并说明理由：
（1）AB=4cm, BC=6cm, AC=8cm, A'B'=12cm, B'C'=18cm, A'C'=24cm;
（2）∠A=120°, AB=7cm, AC=14cm, ∠A'=120°, A'B'=3cm, A'C'=6cm.
∴ △ABC∽△A'B'C'
1.根据下列条件，判断△ABC与△A'B'C'是否相似，并说明理由：
（1）∠A=40°, AB=8cm, AC=15cm, ∠A'=40°, A'B'=16cm, A'C'=30cm.
（2）AB=10cm, BC=8cm, AC=16cm, A'B'=16cm, B'C'=12.8cm, A'C'=25.6cm;
相似，因为两边成比例，夹角相等.
相似，因为三边成比例.
2.图中的两个三角形是否相似？为什么？
1.（1）判断图1中两三角形是否相似；
解：（1）相似. 设小方格边长为1，则AB=2, BC=2 ，AC=2 ,EF=2，ED= , DF= .∵ ∴△DEF∽△ABC.
（2）求图2中x和y的值.
∴∠B=∠D=98°，
∴x=40.5 y=98
2.如图，△ABC中，D、E分别是AB、AC上的点，且AD=5，DE=4，AE= , DB=7，BC= ,EC= , 那么△ADE∽△ABC吗？为什么？
解： △ADE∽△ABC
∴ △ADE∽△ABC
3.如图，已知△ABD∽△ACE．求证：△ABC∽△ADE.
证明：∵ △ABD∽△ACE∴∠BAD=∠CAE,∴∠BAD+∠DAC= ∠CAE+ ∠DAC即∠BAC=∠DAE. 又∵∴△ABC∽△ADE.
相似三角形的两条判定定理
在△ABC中,∠B=30°，AB=5cm，AC=4cm，在△A′B′C′中，∠B′=30°，A′B′=10cm，A′C′=8 cm，这两个三角形一定相似吗？若相似，说说是用哪个判定方法;若不相似，请说明理由.
解：不一定. 虽然∠B=∠B', 但∠B和∠B'不是对应边的夹角，∴这两个三角形不一定相似.（见知识点2思考）