（江苏省无锡市专用）备战2021年中考数学押题卷（试题 答案）

这是一份（江苏省无锡市专用）备战2021年中考数学押题卷（试题 答案），共21页。

无锡市备战2021年中考数学押题卷
一、选择题（本大题共10小题，每小题3分，共计30分.在每小题所给出的四个选项中，恰有一项是符合题目要求的.)
1．(本题3分)的相反数是（ ）
A．9 B． C． D．6
2．(本题3分)化简的结果是（ ）
A． B． C． D．
3．(本题3分)下列汽车的徽标中，是中心对称图形的是 （ ）
A． B． C． D．
4．(本题3分)有一组数据：．这组数据的中位数是（ ）
A． B． C． D．
5．(本题3分)如图是由5个相同的小立方块组成的立体图形，则它的俯视图是（ ）

A． B． C． D．
6．(本题3分)如图，在△ABC中，点D在AB边上，且AD=2BD，过点D作DE∥BC交AC于点E，若AE=2，则AC的长是（ ）

A．4 B．3 C．2 D．1
7．(本题3分)一元二次方程根的判别式的值为（ ）
A．8 B．-8 C． D．
8．(本题3分)在四边形ABCD中，如果∠A＋∠B＋∠C=260°，那么∠D的度数为（ ）

A．120° B．110° C．100° D．90°
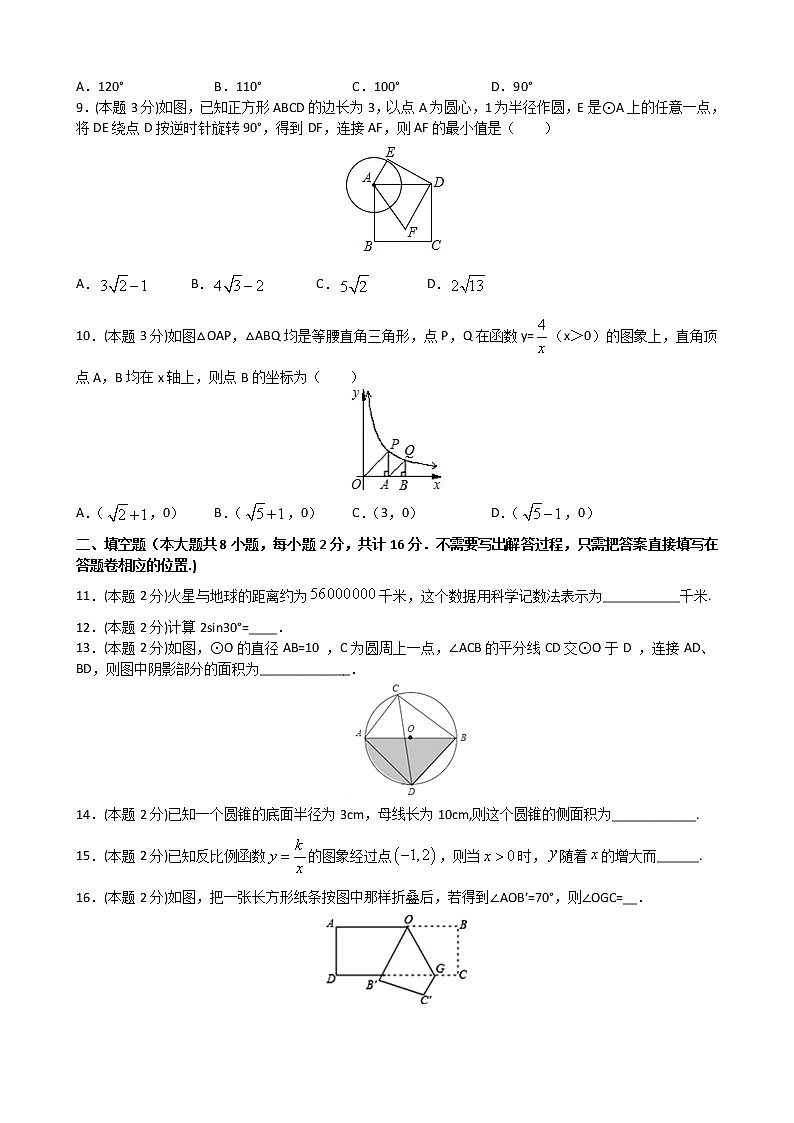
9．(本题3分)如图，已知正方形ABCD的边长为3，以点A为圆心，1为半径作圆，E是⊙A上的任意一点，将DE绕点D按逆时针旋转90°，得到DF，连接AF，则AF的最小值是（ ）

A． B． C． D．
10．(本题3分)如图△OAP，△ABQ均是等腰直角三角形，点P，Q在函数y=（x＞0）的图象上，直角顶点A，B均在x轴上，则点B的坐标为（　　）

A．（，0） B．（，0） C．（3，0） D．（，0）
二、填空题（本大题共8小题，每小题2分，共计16分．不需要写出解答过程，只需把答案直接填写在答题卷相应的位置.)
11．(本题2分)火星与地球的距离约为千米，这个数据用科学记数法表示为___________千米.
12．(本题2分)计算2sin30°=____．
13．(本题2分)如图，⊙O的直径AB=10 ，C为圆周上一点，∠ACB的平分线CD交⊙O于D ，连接AD、BD，则图中阴影部分的面积为_____________．

14．(本题2分)已知一个圆锥的底面半径为3cm，母线长为10cm,则这个圆锥的侧面积为____________.
15．(本题2分)已知反比例函数的图象经过点，则当时，随着的增大而______.
16．(本题2分)如图，把一张长方形纸条按图中那样折叠后，若得到∠AOB′=70°，则∠OGC=__．

17．(本题2分)已知y=3x-1且0≤x≤，令S=xy，则函数S的取值范围是__．
18．(本题2分)如图，正方形纸片的边长为4，是边的中点，连接，折叠该纸片，使点落在上的点，并使折痕经过点，得到折痕，点在上，则的长为_____．

三、解答题（本大题共10小题，共84分．解答时应写出文字说明、证明过程或演算步骤.)
19．(本题8分)（1）计算：；
（2）先化简，再求值：（-4）÷，其中x=1．





20．(本题8分)已知关于的一元二次方程有两个实数根．
（1）求的取值范围．
（2）若为正整数，且该方程的根都是整数，求的值及方程的根.







21．(本题8分)已知：在△ABC中,∠ABC=60°,CD平分∠ACB交AB于点D,点E在线段CD上(点E不与点C．D重合)，且∠EAC=2∠EBC．
(1)如图1,若∠EBC=27°,且EB=EC,则∠DEB=___°,∠AEC=___°.
(2)如图2，①求证：AE+AC=BC；
②若∠ECB=30°，且AC=BE，求∠EBC的度数．






22．(本题8分)中学时代是人生的黄金时代，是学校体育教育的重要时期.某校为了提高学生的身体素质，积极组织学生参加“阳光大课间”活动，体育老师随机抽取本校的部分同学，调查他们最喜爱的“阳光大课间”活动项目（“阳光大课间”设有跳绳、跳远、广播体操、跑步四个活动项目），并将调查结果绘制成如下两幅不完整的统计图.请结合图中的信息，解答下列问题：

（1）参与调查的学生有______人，扇形统计图中跳绳对应的圆心角度数为______度；
（2）补全条形统计图；
（3）为激发同学们的活动热情，九年级（1）班决定从跳绳、跳远、广播体操、跑步四项活动中随机选取两项进行班级友谊赛，求选取的项目中恰好有跑步的概率.






23．(本题6分)勤俭节约一直是中华民族的传统美德，某中学校团委准备以“勤俭节约”为主题开展一次演讲比赛，为此先对同学们每月零花钱的数额进行一些了解，随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表．
组别
分组（单位：元）
人数
A
0≤x＜30
4
B
30≤x＜60
a
C
60≤x＜90
b
D
90≤x＜120
8
E
120≤x＜150
2
根据以上图表，解答下列问题：
（1）填空：这次调查的同学共有　 　人，a+b＝　 　，m＝　 　；
（2）求扇形统计图中扇形B的圆心角的度数；
（3）该校共有1200名学生，请估计每月零花钱的数额在60≤x＜90范围的人数．


24．(本题8分)已知如图△ABC中，以AB为直径的⊙O与AC，BC的交点分别为D，E．
（1）∠A＝68°，求∠CED的大小.
（2）当DE＝BE时，证明：△ABC为等腰三角形．







25．(本题8分)点在线段上，．
(1) 如图1，，两点同时从，出发，分别以，的速度沿直线向左运动；

①在还未到达点时，的值为 ；
②当在右侧时(点与不重合)，取中点，的中点是，求的值；
(2) 若是直线上一点，且．则的值为 ．













26．(本题10分)如图，已知A，B，C三点的坐标分别为A(0，5)，B(8，0)，C(8，－1)，OB上有一动点P，设P(x，0)．
(1)用含x的代数式表示AP＋PC的长；
(2)点P在什么位置(即求P点坐标)时，AP＋PC的长最小？最小值是多少？









27．(本题10分)定义：把函数（m＞0）的图象叫做正值双曲线．把函数（m＜0）的图象叫做负值双曲线．
（1）请写出正值双曲线的两条性质；
（2）如图，直线l经过点A（﹣1，0），与负值双曲线（m＜0）交于点B（﹣2，﹣1）．P是射线AB上的一点，过点P作x轴的平行线分别交该负值双曲线于M，N两点（点M在点N的左边）．
①求直线l的解析式和m的值；
②是否存在点P，使得S△AMN＝4S△APM？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由．








28．(本题10分)如图①，已知抛物线y＝ax2﹣4amx+3am2（a、m为参数，且a＞0，m＞0）与x轴交于A、B两点（A在B的左边），与y轴交于点C．
（1）求点B的坐标（结果可以含参数m）；
（2）连接CA、CB，若C（0，3m），求tan∠ACB的值；
（3）如图②，在（2）的条件下，抛物线的对称轴为直线l：x＝2，点P是抛物线上的一个动点，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的的等腰直角三角形．若存在，求出所有符合条件的点P的坐标，若不存在，请说明理由．


参考答案
1．A
【解析】，∴的相反数是9．
故选：A．
2．B
【解析】 ，故选B.
3．A
【解析】A是中心对称图形，符合题意；
B、C、D不是中心对称图形，不符合题意．
故选A．
4．B
【解析】解：这组数据的中位数是40
故选B．
5．C
【解析】几何体的俯视图是C中图形，故选C．
6．B
【解析】由平行线分线段成比例定理得出比例式可得=2，求出CE=AE=1，即可得出AC=AE+CE=3；
故选B．
7．B
【解析】
故答案为：B．
8．C
【解析】∵在四边形ABCD中,∠A+∠B+∠C+∠D=360°,且∠A+∠B+∠C=260°，
∴∠D=100°，
故选C
9．A
【解析】如图1，连接FC，AF，

∵ED⊥DF，
∴∠EDF=∠EDA+∠ADF=90°，
∵四边形ABCD是正方形，
∴AD=CD，∠ADC=90°，
∴∠ADF+∠CDF=90°，
∴∠EDA=∠CDF，
在△ADE和△CDF中，
∵，
∴△ADE≌△CDF，
∴CF=AE=1，
∴AF＞AC-CF，即AF＞AC-1，
∴当F在AC上时，AF最小，如图2，

∵正方形ABCD的边长为3，
∴AC=3，
∴AF的最小值是3-1；
故选A．
10．B
【解析】解：∵△OAP是等腰直角三角形，
∴PA=OA ，
∴设P点的坐标是（a，a），
把（a，a）代入解析式得到a=2，
∴P的坐标是（2，2），
则OA=2，
∵△ABQ是等腰直角三角形，
∴BQ=AB，
∴设点Q的纵坐标是b，
∴点Q的横坐标是b+2，
把Q的坐标代入解析式y=，
∴，
∴b=﹣1，
∴b+2=﹣1+2=+1，
∴点B的坐标为（+1，0），
故选：B．
11．
【解析】用科学记数法表示为：
故答案为：
12．1．
【解析】原式=2×=1．故答案为1．
13．
【解析】详解：如图，连接OD．
∵AB是直径，且AB=10，∴∠ACB=90°，AO=BO=DO=5．
∵CD平分∠ACB，∴∠ABD=∠ACD=∠ACB=45°，∴∠AOD=90°，则阴影部分的面积是S扇形AOD+S△BOD=+×5×5=+．
故答案为：+．

14．30πcm2.
【解析】这个圆锥的侧面积=π×3×10=30πcm2.
故答案为30πcm2.
15．增大
【解析】解：将点（-1,2）代入解析式得，
k=xy=-1×2=-2，
则函数解析式为故函数图象位于二、四象限，
∴当x＞0时，y随x的增大而增大．
故答案为：增大．
16．125°
【解析】解：∵四边形OB′C′G由四边形OBCG折叠而成，∠AOB′=70°，
∴∠BOG== = 55°，
∵AB∥CD，
∴∠OGC=180°-55°=125°．
故答案为125°．
17．≤S≤
【解析】∵y=3x－1，S=xy，
∴S=x（3x－1）=3x2－x


∵0≤x≤，
∴≤S≤，
故答案为：≤S≤.
18．
【解析】解：在正方形ABCD中，∠BAD=∠D =90°，

∴∠BAM+∠FAM=90°，
又∵是边的中点，
∴DE=2，
在Rt△ADE中，AE=
∵由折叠的性质可得△ABF≅△GBF，
∴AB=BG，∠FBA=∠FBG
∴BF垂直平分AG，
∴AM=MG，∠AMB=90°，
∴∠BAM+∠ABM=90°，
∴∠ABM=∠FAM
∴△ABM~△ADE，
∴= ，
∴= ，
∴AM=，  
 ∴AG=，
∴GE=AE-AG=-=．
19．（1）-1；（2）x-2，-1
【解析】解：（1）原式=
==
=-1；
（2）原式=•
=•
=x-2，
当x=1时，原式=1-2=-1．
20．（1）；（2）的值为或，方程的根为，．
【解析】（1）由题意：b2-4ac≥0，
即：22-4(2k-4)≥0，
所以；
（2）因为，为正整数，
所以k=1或k=2，
当k=1时，原方程为：x2+2x-2=0，
（x+1）2=3，
解得：x=，
因为方程的根为整数，所以x=不符合题意，舍去；
当k=2时，原方程为：x2+2x=0，
解得：，，均为整数，符合题意，
综上，的值为或，方程的根为，．
21．（1）27°,99°;（2）①见解析；②20°；
【解析】(1)∵EB=EC，
∴∠EBC=∠ECB=27°，
∵CD平分∠ACB，
∴∠ACD=∠ECB=27°，
∵∠EAC=2∠EBC=54°，
∴∠AEC=180°−27°−54°=99°，
故答案为27°,99°;
(2)①证明：如图1，在BC上取一点M，使BM=ME，

∴∠MBE=∠MEB，
∵∠EAC=2∠MBE，∠EMC=∠MBE+∠MEB=2∠MBE，
∴∠EAC=∠EMC，
在△ACE与△MCE中，
，
∴△ACE≌△MCE，
∴AE=ME，CM=AC，
∴AE=BM，
∴BC=BM+CM=AE+AC；
②如图2在BC上取一点M,使BM=ME,连接AM,

∵∠ECB=30°，
∴∠ACB=60°,由①可知;△AMC是等边三角形(M点与B点重合)，
∴AM=AC=BE，
在△EMB与△MEA中，
，
∴∠EBC=∠MAE，
∵∠MAC=60°，
∵∠EAC=2∠EBC=2∠MAE，
∴∠MAE=20°,∠EAC=40°，
∴∠EBC=20°.
22．（1）120，144；（2）详见解析；（3）.
【解析】（1）由条形统计图可知喜欢广播体操的学生有30人，由扇形统计图可知喜欢广播体操的人数占调查总人数的，
∴参与调查的学生总人数为（人）；
由条形统计图可知喜欢跳绳的学生有48人，
∴扇形统计图中跳绳对应的圆心角度数为.
故答案为：120，144；
（2）喜欢跳远的学生人数为（人），
补全条形统计图如图：

（3）将跳绳、跳远、广播体操、跑步分别用、、、表示，列表如下：

























由列表可知共有12种等可能的结果，其中九年级（1）班选取项目中有跑步的结果有6种，则（九年级（1）班选取的项目中恰好有跑步）.
故答案为：.
23．（1）50，36,52；（2）72°；（3）864.
【解析】解：（1）∵被调查的同学共有4÷8%＝50人，
∴a＝50×20%＝10，b＝50﹣（4+10+8+2）＝26，
则a+b＝36，m%＝×100%＝52%，即m＝52，
故答案为50、36、52；
（2）扇形统计图中扇形B的圆心角的度数为360°×20%＝72°；
（3）估计每月零花钱的数额在60≤x＜90范围的人数为1200×＝864人．
24．（1）∠CED＝68°；（2）证明见解析.
【解析】（1）∵四边形ABED为⊙O的内接四边形，
∴∠A+∠BED＝180°，
∵∠BED+∠CED=180°，∠A=68°，
∴∠CED＝∠A＝68°.
（2）∵AB为直径，
∴∠ADB＝90°，
∵ED＝EB，
∴∠EDB＝∠EBD，
∵∠CDE+∠EDB＝90°，∠C+∠EBD＝90°，
∴∠C＝∠CDE，
∵四边形ABED为⊙O的内接四边形，
∴∠ADE+∠ABC=180°，
∵∠CDE+∠ADE=180°，
∴∠CDE＝∠ABC，
∴∠C＝∠ABC，
∴△ABC为等腰三角形．
25．（1）①；②;（2）或或或
【解析】解：（1）①AP=AC-PC，CQ=CB-QB，
∵BC=2AC，P、Q速度分别为1cm/s、2cm/s，
∴QB=2PC，
∴CQ=2AC-2PC=2AP，
∴
②设运动秒
，
分两种情况
A:在右侧，
，分别是，的中点
，，

∴
B:在左侧，
，分别是，的中点
，，

∴
（2）∵BC=2AC．
设AC=x，则BC=2x，
∴AB=3x，
①当D在A点左侧时，
|AD-BD|=BD-AD=AB=CD，
∴CD=6x，
∴ ；
②当D在AC之间时，
|AD-BD|=BD-AD=CD，
∴2x+CD-x+CD=CD，
x=-CD（不成立），
③当D在BC之间时，
|AD-BD|=AD-BD=CD，
∴x+CD-2x+CD=CD，
CD=x，
∴；
|AD-BD|=BD-AD=CD，
∴2x-CD-x-CD=CD，
∴CD=
；
④当D在B的右侧时，
|AD-BD|=BD-AD=CD，
∴2x-CD-x-CD=CD，
CD=6x，
∴．
综上所述，的值为或或或
26．（1）AP＋PC＝＋；（2）当点P的坐标为 时，AP＋PC的长最小，AP＋PC的长的最小值是10.
【解析】解：由勾股定理得：
AP＝＝，
CP＝＝，
所以AP＋PC＝＋.
(2)如图，当点P为线段AC与线段OB的交点时，AP＋PC的长最小．

设直线AC对应的函数表达式为y＝kx＋5.
将点C(8，－1)代入得k＝－，所以y＝－x＋5.
当y＝0时，x＝，所以P，
即当点P的坐标为时，AP＋PC的长最小．
此时，AP＋PC的长即为线段AC的长．AC＝＝10.
所以AP＋PC的长的最小值是10.
27．（1）①当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而减小；②无论x取何值，y＞0；③图象与坐标轴没有交点；④图象分布在第一、二象限，等等；（2）①m的值为﹣2；②P 和，
【解析】解：（1）①当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而减小；②无论x取何值，y＞0；③图象与坐标轴没有交点；④图象分布在第一、二象限，等等；
（2）①设直线l的解析式为y＝kx+b．
∵直线l过点A（﹣1，0）和点B（﹣2，﹣1），
∴解得，
∴直线l的解析式为y＝x+1．
m的值为﹣2；

②若存在，设点P的坐标为（p，p+1），则点M（，p+1），点N（﹣，p+1）．
∴S△AMN＝|﹣﹣|×|p+1|＝2，
若点P在线段AB上，
则S△APM＝（p﹣）×[﹣（p+1）]＝（﹣P2﹣P+2）．
∵S△AMN＝4S△APM，
∴2＝4×（﹣P2﹣P+2），即P2+P﹣1＝0．
解得p1＝，p2＝（舍去），
若点P与点B重合，△APM不存在；
若点P在线段AB的延长线上，则S△APM＝（﹣p）×[﹣（p+1）]＝（P2+P﹣2）．
∵S△AMN＝4S△APM，
∴2＝4×（P2+P﹣2），即P2+P﹣3＝0．
解得p3＝，p4＝（舍去）．
故存在点P（，）和（，），使得S△AMN＝4S△APM．
28．（1）B（3m，0）；（2）tan∠ACB＝；
（3）点P的坐标是：（）或（）或（）或（）．
【解析】解：（1）令y＝0，则有ax2﹣4amx+3am2＝0，
解得：x1＝m，x2＝3m，
∵m＞0，A在B的左边，
∴B（3m，0）；
（2）如图1，过点A作AD⊥BC，垂足为点D，

由（1）可知B（3m，0），则△BOC为等腰直角三角形，
∵OC＝OB＝3m，
∴BC＝3m，
又∵∠ABC＝45°，
∴∠DAB＝45°，
∴AD＝BD，
∵AB＝2m，
∴m，CD＝2m，
∴tan∠ACB＝；
（3）∵由题意知x＝2为对称轴，
∴2m＝2，
即m＝1，
∵在（2）的条件下有（0，3m），
∴3m＝3am2，
解得m＝，即a＝1，
∴抛物线的解析式为y＝x2﹣4x+3，
①当P在对称轴的左边，如图2，过P作MN⊥y轴，交y轴于M，交l于N，

∵△OPF是等腰直角三角形，且OP＝PF，
易得△OMP≌△PNF，
∴OM＝PN，
∵P（m，m2﹣4m+3），
则﹣m2+4m﹣3＝2﹣m，
解得：m＝或，
∴P的坐标为（，）或（）；
②当P在对称轴的右边，
如图3，过P作MN⊥x轴于N，过F作FM⊥MN于M，

同理得△ONP≌△PMF，
∴PN＝FM，
则﹣m2+4m﹣3＝m﹣2，
解得：x＝或；
P的坐标为（）或（）；
综上所述，点P的坐标是：（）或（）或（）或（）．