专题11 新定义问题（4）-2021年中考数学二轮复习经典问题专题训练

专题11  新定义问题（4）

【规律总结】

※知识精要

新定义型问题是学习型阅读理解题，是指题目中首先给出一个新定义（新概念或新公式），通过阅读题

目提供的材料，理解新定义，再通过对新定义的理解来解决题目提出的问题。其主要目的是通过对新定义

的理解与运用来考查学生的自主学习能力，便于学生养成良好的学习习惯。

※要点突破

解决此类题的关键是（1）深刻理解“新定义”——明 确“新定义”的条件、原理、方法、步骤和结论;（2）重视“举例”，利用“举例”检验是否理解和正确运用“新定义”；归纳“举例”提供的做题方法；归纳“举例”提供的分类情况；（3）依据新定义，运用类比、归纳、联想、分类讨论以及数形结合的数学思想方法解决题目中需要解决的问题。

【典例分析】

例1．（2020·江西南昌市·七年级期末）对平面上任意一点(a，b)，定义f，g两种变换：f(a，b)＝(﹣a，b)，如f(1，2)＝(﹣1，2)；g(a，b)＝(b，a)，如g(1，2)＝(2，1)，据此得g[f(5，﹣9)]＝（　　）

A．(5，﹣9) B．(﹣5，﹣9) C．(﹣9，﹣5) D．(﹣9，5)

【答案】C

【分析】

根据f，g两种变换的定义自内而外进行解答即可．

【详解】

解：由题意得，f（5，﹣9）]＝（﹣5，﹣9），

∴g[f（5，﹣9）]＝g（﹣5，﹣9）＝（﹣9，﹣5），

故选：C．

【点睛】

本题考查了新定义坐标变换，根据题意、弄懂两种变换的方法是解答本题的关键．

例2．（2019·浙江省义乌市望道中学七年级月考）对于正数规定，例如，计算__________．

【答案】

【分析】

根据规定式子可得，从而可得，由此即可得．

【详解】

因为对于正数规定，

所以，

所以，

则原式，

，

，

故答案为：．

【点睛】

本题考查了有理数加法运算的规律型问题，根据规定的运算式子，找出规律是解题关键．

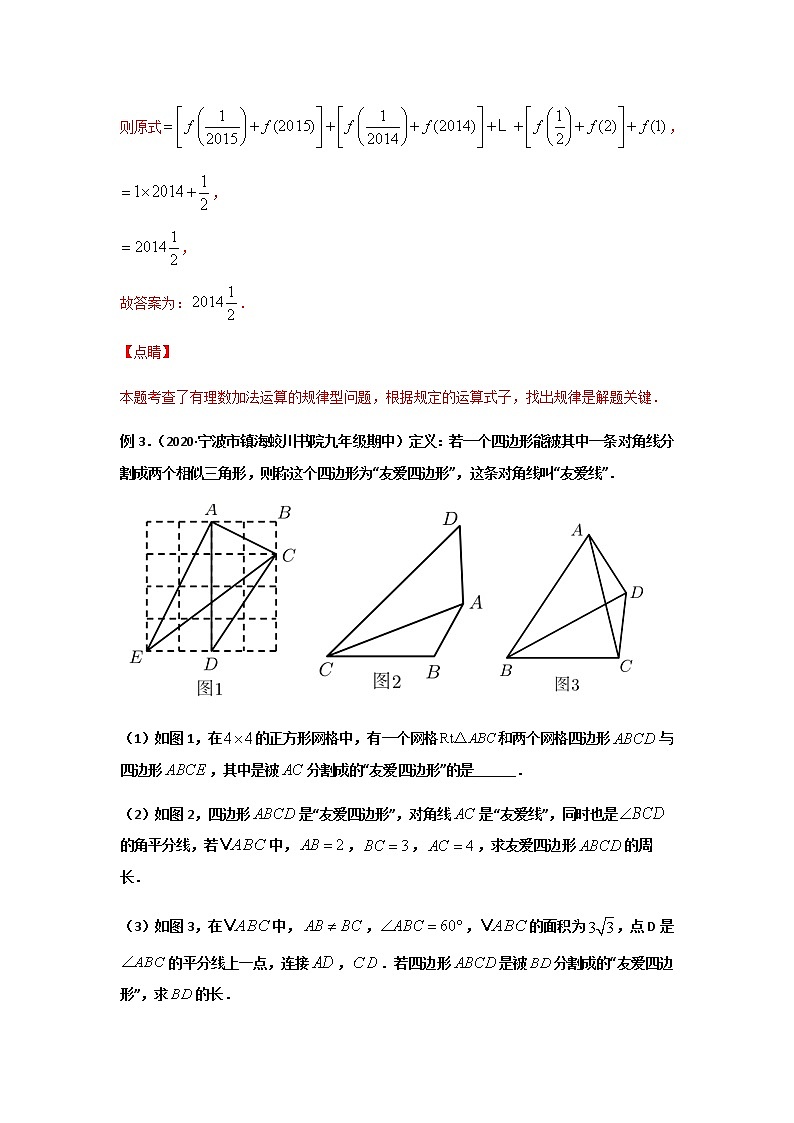
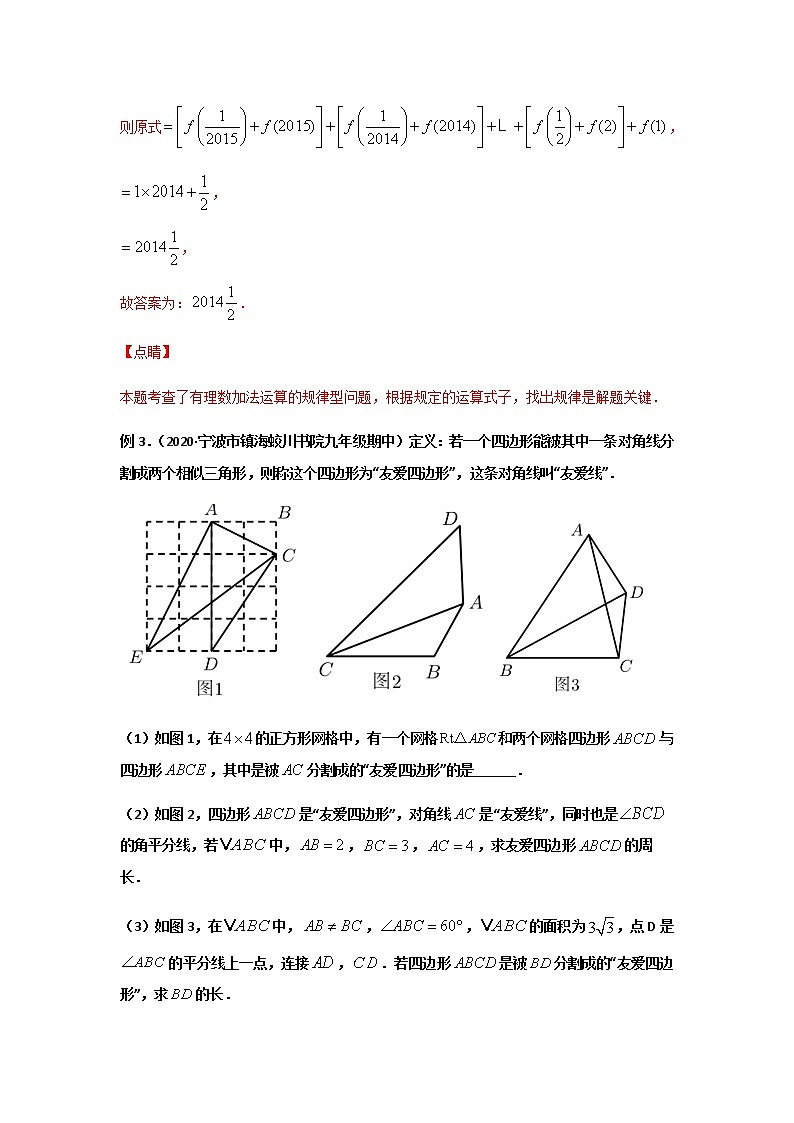
例3．（2020·宁波市镇海蛟川书院九年级期中）定义：若一个四边形能被其中一条对角线分割成两个相似三角形，则称这个四边形为“友爱四边形”，这条对角线叫“友爱线”．

（1）如图1，在的正方形网格中，有一个网格和两个网格四边形与四边形，其中是被分割成的“友爱四边形”的是______．

（2）如图2，四边形是“友爱四边形”，对角线是“友爱线”，同时也是的角平分线，若中，，，，求友爱四边形的周长．

（3）如图3，在中，，，的面积为，点D是的平分线上一点，连接，．若四边形是被分割成的“友爱四边形”，求的长．

【答案】（1）四边形ABCE；（2）13或10；（2）2

【分析】

（1）根据勾股定理分别求出三个三角形的各边长，根据三边对应成比例的三角形相似、“友爱四边形”的定义判断；

（2）根据旋转变换的性质、平行线的性质、两角相等的两个三角形相似证明；

（3）AM⊥BC，根据含30°的直角三角形的特殊性质及勾股定理用AB表示出AM，根据三角形的面积公式得到BC×AB＝12，根据相似三角形的性质列式计算，得到答案．

【详解】

解：（1）∵AB＝2，BC＝1，AD＝4，

∴由勾股定理得，AC＝＝，CD＝＝，

AE＝＝2，CE＝＝5，

∴＝＝＝，

∴ABC∽EAC，

∴四边形ABCE是“友爱四边形”，

∵≠，

∴ABC与ACD不相似，

∴四边形ABCD不是“友爱四边形”，

故答案为：四边形ABCE；

（2）∵AC平分∠BCD，

∴∠ACB=∠ACD，

当∠B=∠DAC时，ABC∽DAC，

则＝＝，

∵，，，

∴＝＝，

解得AD＝，CD＝，

∴友爱四边形的周长为；

当∠B=∠D时，ABC∽ADC，

则＝＝＝1，

∵，，，

∴＝＝1，

解得AD＝2，CD＝3，

∴友爱四边形的周长为，

综上所述，友爱四边形的周长为13或10；

（3）如图3，过点A作AM⊥BC于M，

则∠AMB＝90°，

∵，

∴∠BAM＝30°，

∴BM＝AB，

∴在Rt△ABM中，AM＝

＝

＝AB，

∵ABC的面积为3，

∴BC×AB＝3，

∴BC×AB＝12，

∵四边形ABCD是被BD分割成的“友爱四边形”，且AB≠BC，

∴ABD∽DBC

∴，

∴BD2＝AB×BC＝12，

∴BD＝＝2．

【点睛】

本题考查的是相似三角形的判定和性质、旋转变换的性质、三角形的面积计算，掌握相似三角形的判定定理和性质定理、理解“友爱四边形”的定义是解题的关键．

【好题演练】

一、单选题

1．（2020·广东深圳市·九年级二模）定义：在平面直角坐标系中，过一点分别作坐标轴的垂线，若与坐标轴围成的周长与面积相等，则这个点叫做和谐点，这个矩形叫做和谐矩形．已知点P(m，n)是抛物线y＝x2+k上的和谐点，对应的和谐矩形的面积为16，则k的值可以是（    ）

A．﹣12 B．0 C．4 D．16

2．（2020·全国八年级专题练习）在平面直角坐标系中，对于点和点，给出下列定义：若，则称点为点的限变点，例如：点的限变点的坐标是，点的限变点的坐标是，如果一个点的限变点的坐标是，那个这个点的坐标是（    ）

A． B． C． D．

二、填空题

3．（2020·全国七年级单元测试）我们规定：若关于x的一元一次方程ax＝b的解为b+a，则称该方程为“和解方程“．

例如：方程2x＝﹣4的解为x＝﹣2，而﹣2＝﹣4+2，则方程2x＝﹣4为“和解方程”．请根据上述规定解答下列问题：

（1）已知关于x的一元一次方程3x＝a是“和解方程”，则a的值为_____；

（2）已知关于x的一元一次方程﹣2x＝ab+b是“和解方程“，并且它的解是x＝b，则a+b的值为_____．

4．（2020·浙江杭州市·九年级）已知两个正数a，b，可按规则扩充为一个新数c在a，b，c三个数中取两个较大的数，按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作，（1）若，按上述规则操作三次，扩充所得的数是_________；（2）若，经过6次操作后扩充所得的数为（m，n为正整数），则的值为________．

三、解答题

6．（2020·首都师范大学附属育新学校九年级月考）在平面直角坐标系中，旋转角满足，对图形与图形给出如下定义：将图形绕原点逆时针旋转得到图形．为图形上任意一点，为图形上的任意一点，称长度的最小值为图形与图形的“转后距”．已知点，点，点．

（1）当时，记线段为图形．

①画出图形；

②若点为图形，则“转后距”为_________；

③若线段为图形，求“转后距”；

（2）已知点在点的左侧，点，记线段为图形，线段为图形，对任意旋转角，“转后距”大于1，直接写出的取值范围．

6．（2020·成都市田家炳中学七年级期中）阅读理解：定义：A，B，C为数轴上三点，若点C到点A的距离是它到点B的时距离的n（n为大于1的常数）倍，则称点C是（A，B）的n倍点，且当C是（A，B）的n倍点或（B，A）的n倍点时，我们也称C是A和B两点的n倍点．例如，在图1中，点C是（A，B）的2倍点，但点C不是（B，A）的2倍点．

（1）特值尝试．

①若，图1中，点________是（D，C）的2倍点．（填A或B）

②若，如图2，M，N为数轴上两个点，点M表示的数是，点N表示的数是4，数________表示的点是（M，N）的3倍点．

（2）周密思考：

图2中，一动点P从N出发，以每秒2个单位的速度沿数轴向左运动t秒，若P恰好是M和N两点的n倍点，求所有符合条件的t的值．（用含n的式子表示）

（3）拓展应用：

数轴上两点间的距离不超过30个单位长度时，称这两点处于“可视距离”．若（2）中满足条件的M和N两点的所有n倍点P均处于点N的“可视距离”内，请直接写出n的取值范围．（不必写出解答过程）