



专题50 多线段的最值问题-2021年中考数学二轮复习经典问题专题训练
展开专题50 多线段的最值问题
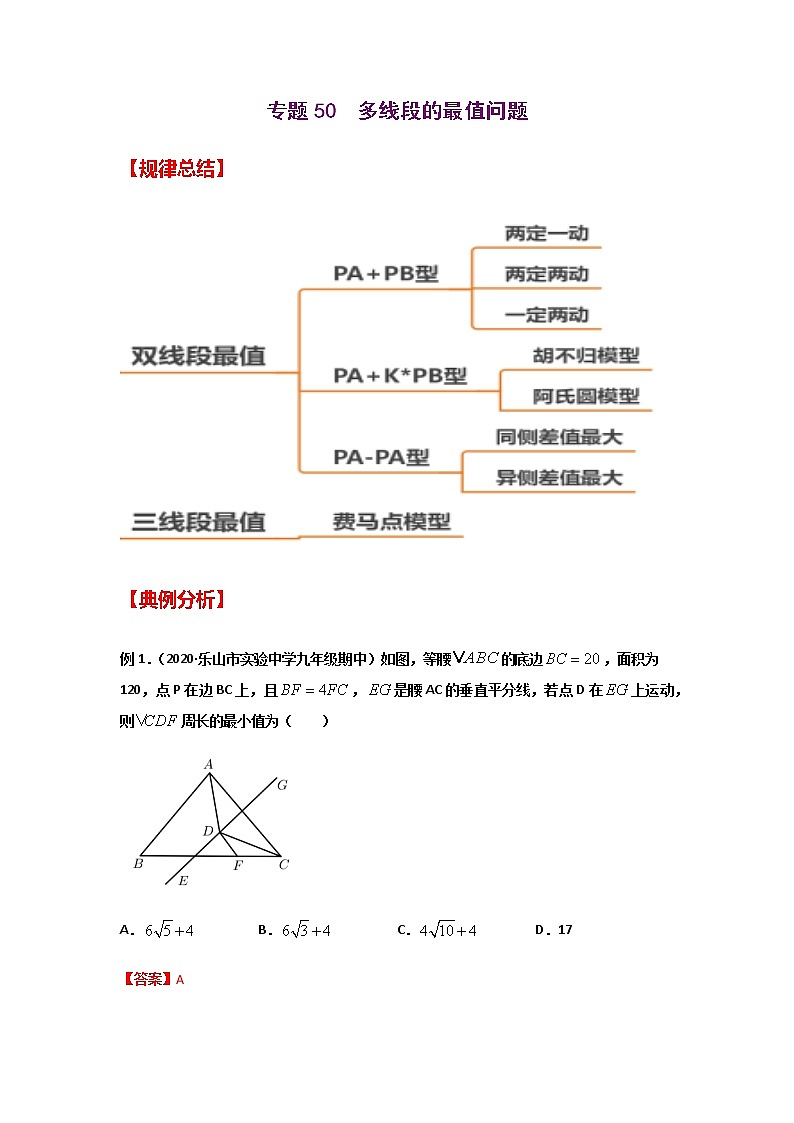
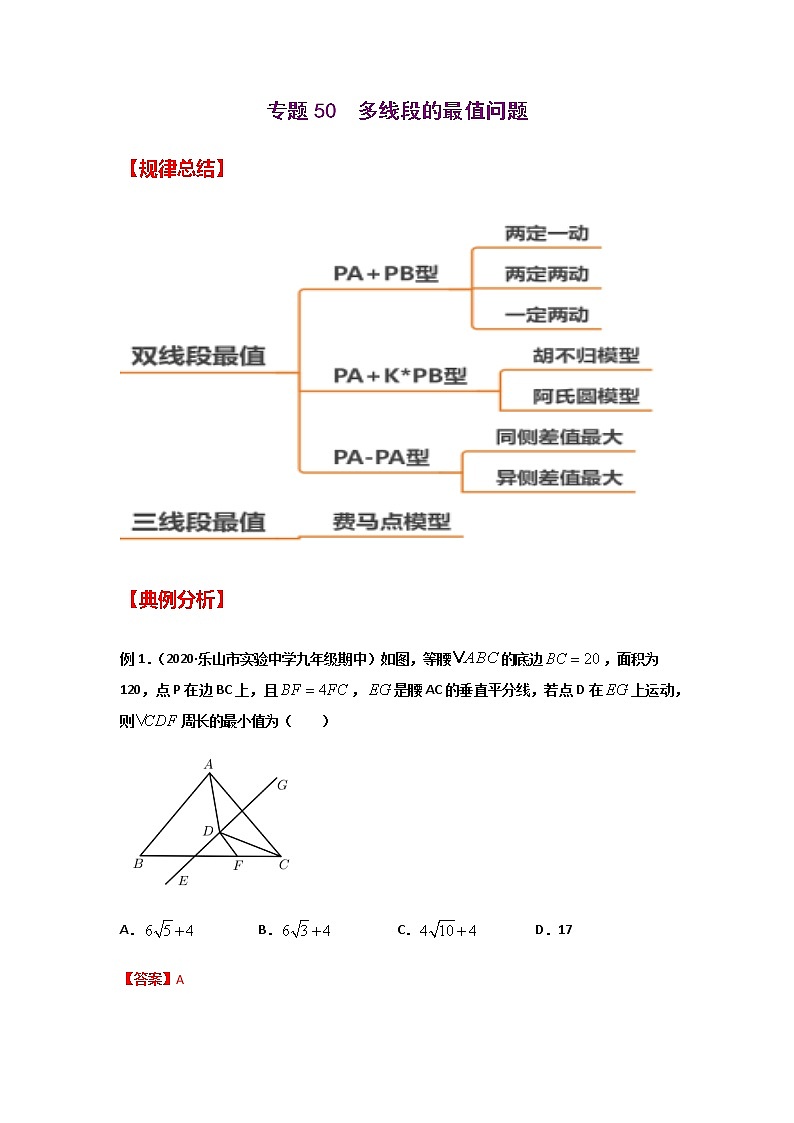
【规律总结】
【典例分析】
例1.(2020·乐山市实验中学九年级期中)如图,等腰的底边,面积为120,点P在边BC上,且,是腰AC的垂直平分线,若点D在上运动,则周长的最小值为( )
A. B. C. D.17
【答案】A
【分析】
根据题意连接交与,再依据垂直平分线性质得出,进而利用两点间线段最短求出AF的值即可得出周长的最小值.
【详解】
解:如图,连接交与,
因为是的垂直平分线,所以,
的周长,
因为为定值,
所以当最小时,周长最小
因为两点之间线段最短,所以最小值为,
过作于点,
因为,所以,
因为面积为,,所以,
因为,所以,
,
在中,
根据勾股定理得,,
所以,
所以的周长.
故选:A.
【点睛】
本题考查等腰三角形和垂直平分线性质,熟练掌握垂直平分线上到两个端点的距离相等以及等腰三角形三线合一的性质是解题的关键.
例2.(2020·浙江嘉兴市·八年级期末)如图,内有一定点P,且,在上有一动点Q,上有一动点R,若周长最小,则最小周长是___________.
【答案】
【分析】
作点P关于OA的对称点,关于OB的对称点,连接与OA、OB分别相交于点Q、R,根据轴对称的性质可得,,从而得到△PQR的周长,并且此时有最小值,连接,再求出为等腰直角三角形,再根据等腰直角三角形的性质求解即可.
【详解】
解:如图,作点P关于OA的对称点,关于OB的对称点,
连接与OA、OB分别相交于点Q、R,
所以,,,
所以,的周长,
由两点之间线段最短得,此时周长最小,
连接,
则
所以,
所以,为等腰直角三角,
所以,,
即最小周长是.
故答案为.
【点睛】
本题考查了轴对称确定最短路线问题,轴对称的性质,等腰直角三角形的判定与性质,勾股定理的应用,难点在于作辅助线得到与周长相等的线段.
例3.(2020·浙江金华市·九年级期末)如图1,抛物线与x轴交于点,与y轴于点B,在x轴上有动点,过点E作x轴的垂线交直线于点N,交抛物线于点P,过点P作于点M.
(1)求a的值和直线的函数表达式;
(2)设的周长为的周长为,若,求m的值;
(3)如图2,当,将线段绕点O逆时针旋转得到,旋转角为,连接,求的最小值.
【答案】(1),;(2)m=;(3).
【分析】
(1)把点代入抛物线解析式,得方程即可求出a,再根据AB两点用待定系数法可以确定直线AB解析式;
(2)由△PNM∽△ANE,推出,列出方程即可解决问题;
(3)在y轴上 取一点使得,构造相似三角形,可以证明就是的最小值
【详解】
解:(1)把点代入抛物线解析式得:16a+4(a+3)+3=0,
解得:,
∴抛物线解析式为:,
∴A(4,0),B(0,3),
设直线AB解析式为y=kx+b,则,
解得,
∴直线AB解析式为
(2)如图1,
∵PM⊥AB,PE⊥OA,
∴∠PMN=∠AEN,
∵∠PNM=∠ANE,
∴△PNM∽△ANE,
∵NE//OB,
,
∵A(4,0),B(0,3),
∴,,
∴,
∴,
∵抛物线解析式为,
∴,
∴,
解得m=或4,
经检验m=4是分式方程的增根,
∴m=;
(3)如图2,在y轴上 取一点使得连接,
∵,,
∴,
,
∵ ,
∴,
,
∴,
∴,
∴当B、、三点共线时,最小(两点间线段最短),此时旋转角为,
即最小值=.
【点睛】
本题主要考查了二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、一次函数的解析式、相似三角形的性质和判定、旋转的性质,列出关于m的方程是解题答问题(2)的关键,解题的关键是构造相似三角形,找到线段就是.
【好题演练】
一、单选题
1.(2020·广西贵港市·中考真题)如图,动点在边长为2的正方形内,且,是边上的一个动点,是边的中点,则线段的最小值为( )
A. B. C. D.
2.(2021·广东肇庆市·八年级期末)如图,等边△ABC中,BD⊥AC于D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为( )
A.3cm B.4cm C.5cm D.6cm
二、填空题
3.(2020·广州白云广雅实验学校九年级月考)如图,在平面直角坐标系中,抛物线的顶点为D,且与轴分别交于A、B两点(点A在点B的左边),P为抛物线对称轴上的动点,则的最小值是_____
4.(2020·陕西渭南市·九年级期末)如图,是⊙的一条弦,点是⊙上一动点,且,点、分别是、的中点,直线与⊙交于、两点,若⊙的半径为,则的最大值为_______
三、解答题
5.(2021·渝中区·重庆巴蜀中学八年级期末)已知:如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,直线分别交x轴,y轴于点D,E,且直线于点C.
(1)如图1,在y轴上有一长为的线段(点P在点Q上方),当线段在y轴正半轴移动时,求的最小值.
(2)如图2,将沿直线方向平移至点E恰好位于x轴上时,记作,再将绕点逆时针旋转,旋转角度为,旋转中的三角形记作,在旋转过程中,边所在的直线分别交直线于点K,H,当为等腰三角形时,请求出点的坐标.
6.(2020·辽宁沈阳市·九年级期末)如图,在边长为16的菱形中,、为对角线,,点、分别是边、边上的动点,连接、、.
(1)当点、点分别是边,边的中点时.
①求证:是等边三角形;
②若点是对角线上的动点,连接,,则直接写出的最小值为______;
(2)若点是对角线上的动点,连接、,则直接写出的最小值为______;
(3)若,交于点,点、点分别是线段、线段上的动点,连接、,则直接写出的最小值为______.
中考数学 最值问题经典100题(专题练习): 这是一份中考数学 最值问题经典100题(专题练习),文件包含中考数学初中数学最值问题经典100题教师版专题练习docx、中考数学初中数学最值问题经典100题学生版专题练习docx等2份试卷配套教学资源,其中试卷共152页, 欢迎下载使用。
中考数学二轮复习培优专题42 几何中的最值问题之和长度有关的最值之多线段的最值 (含解析): 这是一份中考数学二轮复习培优专题42 几何中的最值问题之和长度有关的最值之多线段的最值 (含解析),共31页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
中考数学二轮复习培优专题42几何中的最值问题之和长度有关的最值之多线段的最值 (含答案): 这是一份中考数学二轮复习培优专题42几何中的最值问题之和长度有关的最值之多线段的最值 (含答案),共31页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













