人教版数学七年级下册期中综合测评卷(三)

人教版数学七年级下册期中综合测评卷(三)

一、选择题(本大题共10小题,每小题4分,满分40分)

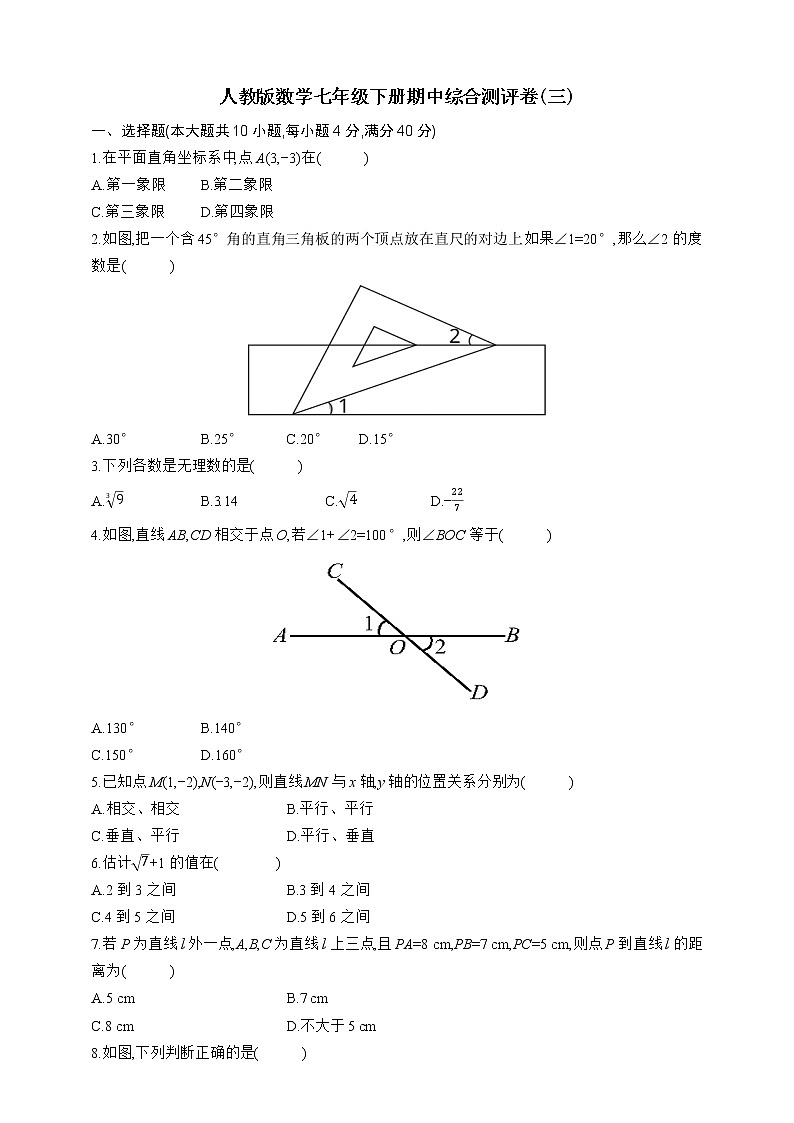
1.在平面直角坐标系中,点A(3,-3)在(      )

A.第一象限 B.第二象限 

C.第三象限 D.第四象限

2.如图,把一个含45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是(      )

A.30° B.25°  C.20° D.15°

3.下列各数是无理数的是(      )

A. B.3.14 C.  D.-

4.如图,直线AB,CD相交于点O,若∠1+∠2=100°,则∠BOC等于(      )

A.130° B.140° 

C.150° D.160°

5.已知点M(1,-2),N(-3,-2),则直线MN与x轴,y轴的位置关系分别为(      )

A.相交、相交          B.平行、平行

C.垂直、平行          D.平行、垂直

6.估计+1的值在(        )

A.2到3之间  B.3到4之间

C.4到5之间  D.5到6之间

7.若P为直线l外一点,A,B,C为直线l上三点,且PA=8 cm,PB=7 cm,PC=5 cm,则点P到直线l的距离为(      )

A.5 cm       B.7 cm

C.8 cm       D.不大于5 cm

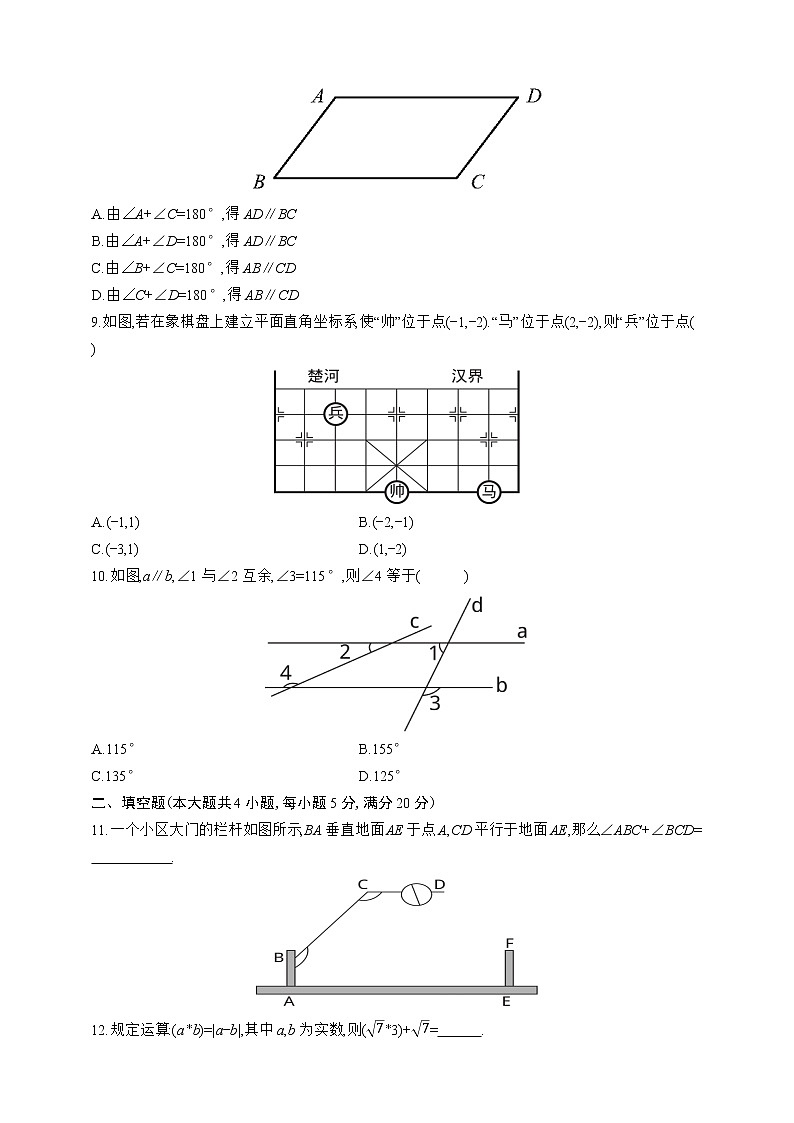
8.如图,下列判断正确的是(      ) 

A.由∠A+∠C=180°,得AD∥BC 

B.由∠A+∠D=180°,得AD∥BC

C.由∠B+∠C=180°,得AB∥CD 

D.由∠C+∠D=180°,得AB∥CD

9.如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2).“马”位于点(2,-2),则“兵”位于点(     )

A.(-1,1)   B.(-2,-1) 

C.(-3,1)   D.(1,-2)

10.如图,a∥b,∠1与∠2互余,∠3=115°,则∠4等于(      )

A.115°   B.155° 

C.135°   D.125°

二、填空题(本大题共4小题,每小题5分,满分20分)

11.一个小区大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,那么∠ABC+∠BCD=　270      　. 

12.规定运算:(a*b)=|a-b|,其中a,b为实数,则(*3)+=　  　. 

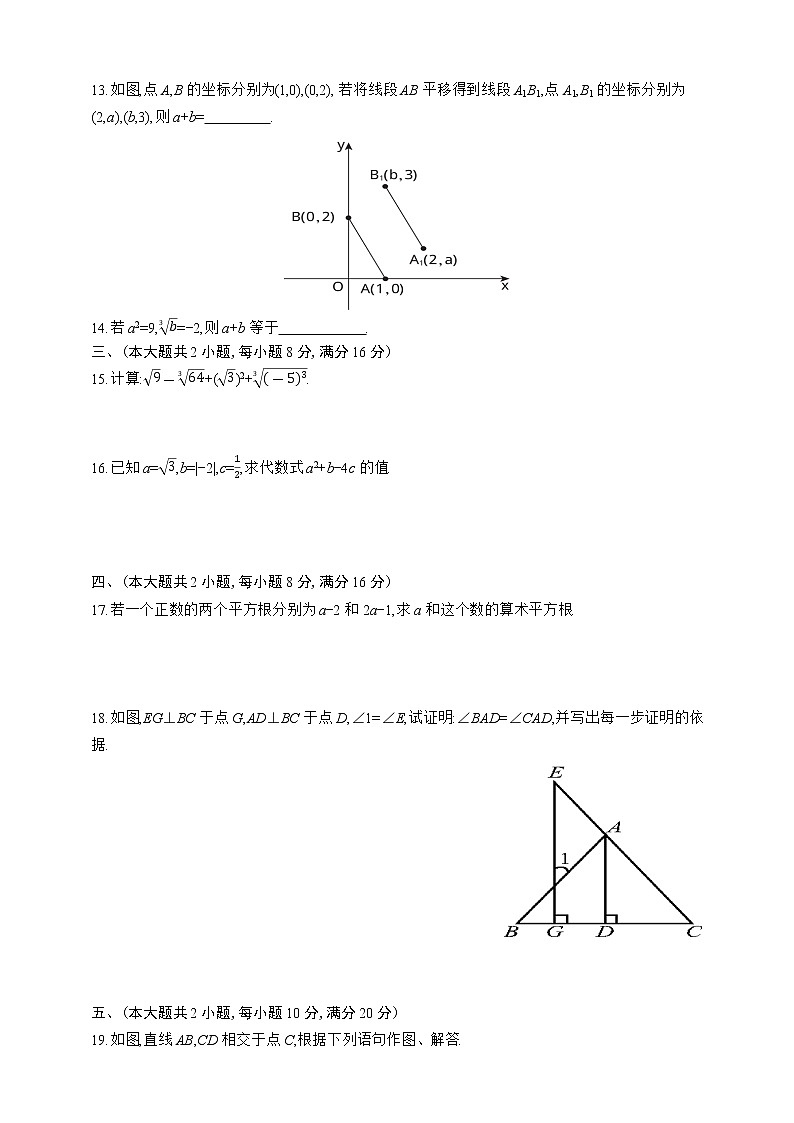
13.如图,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移得到线段A1B1,点A1,B1的坐标分别为(2,a),(b,3),则a+b=　     　. 

14.若a2=9,=-2,则a+b等于　        　.

三、(本大题共2小题,每小题8分,满分16分)

15.计算:+()2+.

16.已知a=,b=|-2|,c=,求代数式a2+b-4c的值.

四、(本大题共2小题,每小题8分,满分16分)

17.若一个正数的两个平方根分别为a-2和2a-1,求a和这个数的算术平方根.

18.如图,EG⊥BC于点G,AD⊥BC于点D,∠1=∠E,试证明:∠BAD=∠CAD,并写出每一步证明的依据.

五、(本大题共2小题,每小题10分,满分20分)

19.如图,直线AB,CD相交于点C,根据下列语句作图、解答.

(1)过点P作PQ∥CD,交AB于点Q;

(2)过点P作PR⊥CD,垂足为R;

(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.

20.在如图所示的网格图中,每个小正方形的边长均为1个单位长度,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,图中的三角形均为格点三角形.根据图形,回答下列问题.

(1)三角形A'B'C'是由三角形ABC通过怎样的变换得到的?

(2)建立恰当的平面直角坐标系,使点A的坐标为(-3,4),并求出三角形DEF的面积S.

六、(满分12分)

21.在平面直角坐标系中,点P从原点O出发,速度为每秒1个单位长度,且点P只能向上或向右运动,请回答下列问题:

(1)将表格填写完整:

(2)当点P从点O出发10秒,可得到的整数点的个数是　   　. 

(3)当点P从点O出发　   　秒时,可得到整数点(10,5). 

七、(满分12分)

22.如图,在矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位长度,得到矩形,第2次平移将矩形沿的方向向右平移5个单位长度,得到矩形,……,第n次平移将矩形沿的方向向右平移5个单位长度,得到矩形(n>2).

(1)求和的长.

(2)若的长为56,求n.

八、(满分14分)

23.如图,已知直线,,点P在直线上且不与点A,B重合.记∠AEP=∠1,∠BFP=∠2,∠EPF=∠3.

(1)若直线∥,当点P在线段AB(A,B两点除外)上运动时,写出∠1,∠2,∠3之间的关系,并说明理由.

(2)若(1)中∠1,∠2,∠3之间的关系成立,你能不能反向推出直线∥?请说明理由.

(3)若直线∥,当点P在直线 (不包括线段AB)上运动时,写出∠1,∠2,∠3之间的关系,并说明理由.

参考答案

一、选择题(本大题共10小题,每小题4分,满分40分)

1.在平面直角坐标系中,点A(3,-3)在(   D   )

A.第一象限 B.第二象限 

C.第三象限 D.第四象限

2.如图,把一个含45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是(   B   )

A.30° B.25°  C.20° D.15°

3.下列各数是无理数的是(   A   )

A. B.3.14 C.  D.-

4.如图,直线AB,CD相交于点O,若∠1+∠2=100°,则∠BOC等于(   A   )

A.130° B.140° 

C.150° D.160°

5.已知点M(1,-2),N(-3,-2),则直线MN与x轴,y轴的位置关系分别为(   D   )

A.相交、相交          B.平行、平行

C.垂直、平行          D.平行、垂直

6.估计+1的值在(   B     )

A.2到3之间  B.3到4之间

C.4到5之间  D.5到6之间

7.若P为直线l外一点,A,B,C为直线l上三点,且PA=8 cm,PB=7 cm,PC=5 cm,则点P到直线l的距离为(   D   )

A.5 cm       B.7 cm

C.8 cm       D.不大于5 cm

8.如图,下列判断正确的是(   C   ) 

A.由∠A+∠C=180°,得AD∥BC 

B.由∠A+∠D=180°,得AD∥BC

C.由∠B+∠C=180°,得AB∥CD 

D.由∠C+∠D=180°,得AB∥CD

9.如图,若在象棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2).“马”位于点(2,-2),则“兵”位于点(   C   )

A.(-1,1)   B.(-2,-1) 

C.(-3,1)   D.(1,-2)

10.如图,a∥b,∠1与∠2互余,∠3=115°,则∠4等于(   B   )

A.115°   B.155° 

C.135°   D.125°

二、填空题(本大题共4小题,每小题5分,满分20分)

11.一个小区大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,那么∠ABC+∠BCD=　270°　. 

12.规定运算:(a*b)=|a-b|,其中a,b为实数,则(*3)+=　3　. 

13.如图,点A,B的坐标分别为(1,0),(0,2),若将线段AB平移得到线段A1B1,点A1,B1的坐标分别为(2,a),(b,3),则a+b=　 2  　. 

14.若a2=9,=-2,则a+b等于　   -5或-11   　.

三、(本大题共2小题,每小题8分,满分16分)

15.计算:+()2+.

解:原式=3-4+3-5=-3.

16.已知a=,b=|-2|,c=,求代数式a2+b-4c的值.

解:a2+b-4c=()2+|-2|-4×=3+2-2=3.

四、(本大题共2小题,每小题8分,满分16分)

17.若一个正数的两个平方根分别为a-2和2a-1,求a和这个数的算术平方根.

解:∵a-2和2a-1是一个正数的两个平方根,

∴a-2+2a-1=0,∴a=1,

∴这个正数为(1-2)2=1,算术平方根为1.

18.如图,EG⊥BC于点G,AD⊥BC于点D,∠1=∠E,试证明:∠BAD=∠CAD,并写出每一步证明的依据.

证明:∵AD⊥BC,EG⊥BC(已知),

∴∠ADC=∠EGC=90°(垂直的定义),

∴AD∥EG(同位角相等,两直线平行),

∴∠1=∠BAD(两直线平行,内错角相等),

∠E=∠CAD(两直线平行,同位角相等).

∵∠1=∠E(已知),

∴∠BAD=∠CAD(等量代换).

五、(本大题共2小题,每小题10分,满分20分)

19.如图,直线AB,CD相交于点C,根据下列语句作图、解答.

(1)过点P作PQ∥CD,交AB于点Q;

(2)过点P作PR⊥CD,垂足为R;

(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.

解:(1)如图所示,直线PQ即为所求.

(2)如图所示,直线PR即为所求.

(3)∠PQC=60°.

理由:因为PQ∥CD,所以∠DCB+∠PQC=180°.

又因为∠DCB=120°,所以∠PQC=180°-120°=60°.

20.在如图所示的网格图中,每个小正方形的边长均为1个单位长度,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,图中的三角形均为格点三角形.根据图形,回答下列问题.

(1)三角形A'B'C'是由三角形ABC通过怎样的变换得到的?

(2)建立恰当的平面直角坐标系,使点A的坐标为(-3,4),并求出三角形DEF的面积S.

解:(1)三角形A'B'C'是由三角形ABC向右平移7个单位长度得到的.

(2)建立平面直角坐标系如图所示.

S=7×2-×7×1-×3×1-×4×2=5.

六、(满分12分)

21.在平面直角坐标系中,点P从原点O出发,速度为每秒1个单位长度,且点P只能向上或向右运动,请回答下列问题:

(1)将表格填写完整:

(2)当点P从点O出发10秒,可得到的整数点的个数是　11　. 

(3)当点P从点O出发　15　秒时,可得到整数点(10,5). 

解:(2)提示:1秒时,有2个整数点;2秒时,有3个整数点;3秒时,有4个整数点;…那么10秒时,应有11个整数点.

(3)提示:横坐标为10,需要从原点开始向右移动10秒,纵坐标为5,需要向上移动5秒,所以需要的时间为15秒.

七、(满分12分)

22.如图,在矩形ABCD中,AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位长度,得到矩形,第2次平移将矩形沿的方向向右平移5个单位长度,得到矩形,……,第n次平移将矩形沿的方向向右平移5个单位长度,得到矩形(n>2).

(1)求和的长.

(2)若的长为56,求n.

解:(1)由题意得=2×6-1=11,

=3×6-2=16.

(2)∵=2×6-1,=3×6-2,=4×6-3,…,

∴=6(n+1)-n=5n+6,

∴5n+6=56,解得n=10.

八、(满分14分)

23.如图,已知直线,,点P在直线上且不与点A,B重合.记∠AEP=∠1,∠BFP=∠2,∠EPF=∠3.

(1)若直线∥,当点P在线段AB(A,B两点除外)上运动时,写出∠1,∠2,∠3之间的关系,并说明理由.

(2)若(1)中∠1,∠2,∠3之间的关系成立,你能不能反向推出直线∥?请说明理由.

(3)若直线∥,当点P在直线 (不包括线段AB)上运动时,写出∠1,∠2,∠3之间的关系,并说明理由.

解:(1)∠3=∠1+∠2.

理由:过点P作PQ∥(点Q在点P的左侧).

∵∥,∴PQ∥∥,

∴∠1=∠QPE,∠2=∠QPF,

∴∠3=∠QPE+∠QPF=∠1+∠2.

(2)可以反向推出直线∥.

理由:过点P作P∥(点在点P的左侧).

∵P∥,∴∠1=∠PE.

∵∠3=∠1+∠2,

∴∠2=∠3-∠1=∠3-∠PE=∠PF,

∴P∥,∴∥.

(3)①当点P在点A的上方时,过点P作P∥,

如图1所示.

∵∥,∴P∥∥,

∴∠1=∠PE,∠2=∠Q2PF,

∴∠3=∠PF-∠PE=∠2-∠1.

②当点P在点B的下方时,过点P作P∥,如图2所示.

∵∥,∴P∥∥,

∴∠1=∠PE,∠2=∠PF,

∴∠3=∠PE-∠PF=∠1-∠2.