人教版数学七年级下册期中综合测评卷(一)

这是一份人教版数学七年级下册期中综合测评卷(一)，共12页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

1.下列命题是假命题的是( )
A.平移不改变图形的形状和大小
B.正数的平方根是正数
C.平行于同一条直线的两条直线平行
D.若a∥b,a⊥c,则b⊥c
2.在实数-1,0,-2,3中,最小的数是( )
A.-1B.0C.-2D.3
3.若-3a=318,则a的值是( )
A.18B.-18C.±18D.-1512
4.图中∠1与∠2互为邻补角的是( )
5.已知点P(a-2,2-b)在第二象限,则点P到y轴的距离为( )
A.a-2 B.2-a
C.b-2 D.2-b
6.下列实数中,在3与4之间的数是( )
A.33B.32C.327D.25
7.在平面直角坐标系中,点A(m,n)经过平移后得到的对应点A'(m+2,n-5)在第二象限,则点A所在的象限是( )
A.第一象限B.第二象限
C.第三象限D.第四象限
8.若a+b-1=0,则(a-b)2021的值为( )
A.1B.-1C.±1 D.0
9.如图,BD为∠ABC的平分线,AD∥BC,∠BDC=90°,∠A与∠C的数量关系为( )
A.∠A=2∠C
B.∠A-12∠C=90°
C.∠A+∠C=180°
D.12∠A+∠C=90°
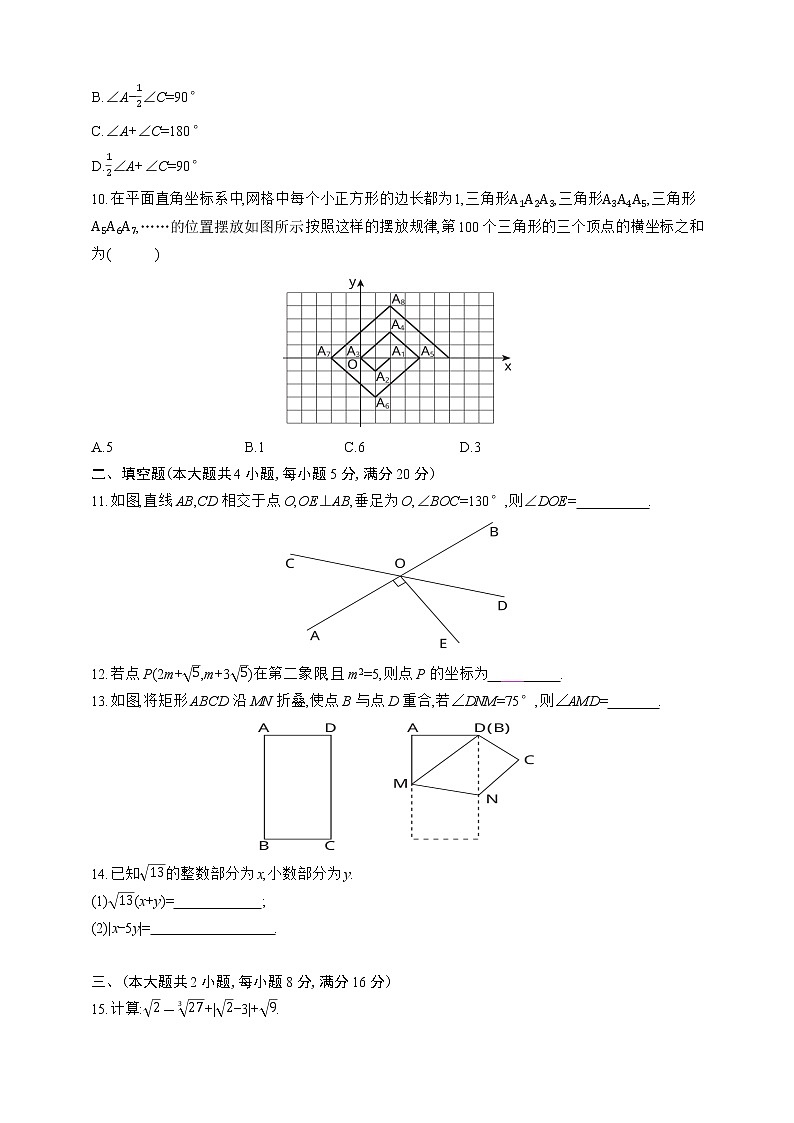
10.在平面直角坐标系中,网格中每个小正方形的边长都为1,三角形A1A2A3,三角形A3A4A5,三角形A5A6A7,……的位置摆放如图所示.按照这样的摆放规律,第100个三角形的三个顶点的横坐标之和为( )
A.5 B.1 C.6 D.3
二、填空题(本大题共4小题,每小题5分,满分20分)
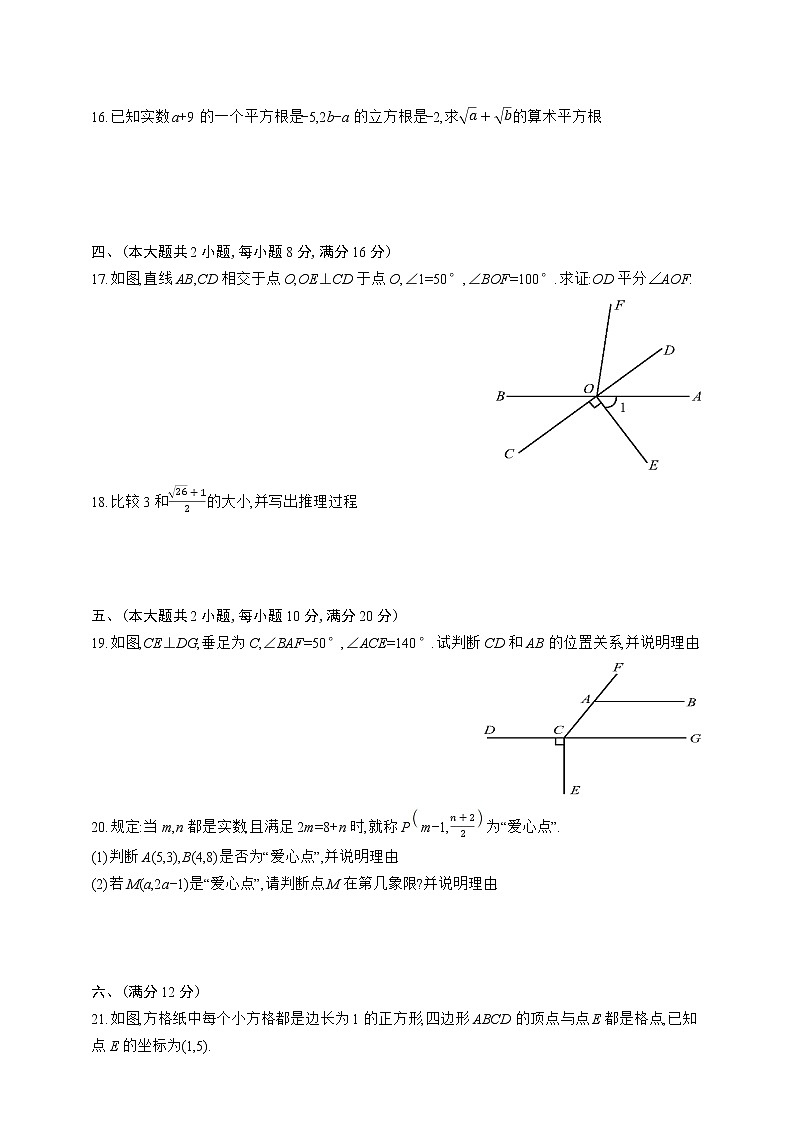
11.如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOC=130°,则∠DOE= .
12.若点P(2m+5,m+35)在第二象限,且m2=5,则点P的坐标为 .
13.如图,将矩形ABCD沿MN折叠,使点B与点D重合,若∠DNM=75°,则∠AMD= .
14.已知13的整数部分为x,小数部分为y.
(1)13(x+y)= ;
(2)|x-5y|= .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2-327+|2-3|+9.
16.已知实数a+9的一个平方根是-5,2b-a的立方根是-2,求a+b的算术平方根.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,直线AB,CD相交于点O,OE⊥CD于点O,∠1=50°,∠BOF=100°.求证:OD平分∠AOF.
18.比较3和26+12的大小,并写出推理过程.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,CE⊥DG,垂足为C,∠BAF=50°,∠ACE=140°.试判断CD和AB的位置关系,并说明理由.
20.规定:当m,n都是实数,且满足2m=8+n时,就称Pm-1,n+22为“爱心点”.
(1)判断A(5,3),B(4,8)是否为“爱心点”,并说明理由.
(2)若M(a,2a-1)是“爱心点”,请判断点M在第几象限?并说明理由.
六、(满分12分)
21.如图,方格纸中每个小方格都是边长为1的正方形,四边形ABCD的顶点与点E都是格点,已知点E的坐标为(1,5).
(1)建立适当的平面直角坐标系,并写出四边形ABCD各顶点的坐标.
(2)若把四边形ABCD向上平移2个单位长度,再向右平移2个单位长度,得到四边形A'B'C'D'.请在图中画出四边形A'B'C'D',并写出四边形A'B'C'D'各顶点的坐标.
(3)求四边形ABCD的面积.
七、(满分12分)
22.如图,在平面直角坐标系中,已知点A的坐标为(a,0),点C的坐标为(b,2),且a,b满足2+a+(b-2)2=0,过点C作CB⊥x轴于点B.
(1)求A,B两点的坐标;
(2)过点B作BD∥AC,交y轴于点D,∠CAB的平分线与∠ODB的平分线相交于点E,求∠AED的度数.
八、(满分14分)
23.(1)如图1,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.
(2)如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由.
(3)如图3,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是 .(直接写出答案,不需要写出过程)
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列命题是假命题的是( B )
A.平移不改变图形的形状和大小
B.正数的平方根是正数
C.平行于同一条直线的两条直线平行
D.若a∥b,a⊥c,则b⊥c
2.在实数-1,0,-2,3中,最小的数是( C )
A.-1B.0C.-2D.3
3.若-3a=318,则a的值是( B )
A.18B.-18C.±18D.-1512
4.图中∠1与∠2互为邻补角的是( D )
5.已知点P(a-2,2-b)在第二象限,则点P到y轴的距离为( B )
A.a-2 B.2-a
C.b-2 D.2-b
6.下列实数中,在3与4之间的数是( C )
A.33B.32C.327D.25
7.在平面直角坐标系中,点A(m,n)经过平移后得到的对应点A'(m+2,n-5)在第二象限,则点A所在的象限是( B )
A.第一象限B.第二象限
C.第三象限D.第四象限
8.若a+b-1=0,则(a-b)2021的值为( B )
A.1B.-1C.±1 D.0
9.如图,BD为∠ABC的平分线,AD∥BC,∠BDC=90°,∠A与∠C的数量关系为( A )
A.∠A=2∠C
B.∠A-12∠C=90°
C.∠A+∠C=180°
D.12∠A+∠C=90°
10.在平面直角坐标系中,网格中每个小正方形的边长都为1,三角形A1A2A3,三角形A3A4A5,三角形A5A6A7,……的位置摆放如图所示.按照这样的摆放规律,第100个三角形的三个顶点的横坐标之和为( C )
A.5 B.1 C.6 D.3
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOC=130°,则∠DOE= 40°.
12.若点P(2m+5,m+35)在第二象限,且m2=5,则点P的坐标为 (-5,25) .
13.如图,将矩形ABCD沿MN折叠,使点B与点D重合,若∠DNM=75°,则∠AMD= 30° .
14.已知13的整数部分为x,小数部分为y.
(1)13(x+y)= 13 ;
(2)|x-5y|= 513-18 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2-327+|2-3|+9.
解:原式=2-3+3-2+3=3.
16.已知实数a+9的一个平方根是-5,2b-a的立方根是-2,求a+b的算术平方根.
解:由题可知a+9=25,2b-a=-8,解得a=16,b=4,
∴a+b=16+4=6.
∵6的算术平方根是6,
∴a+b的算术平方根是6.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,直线AB,CD相交于点O,OE⊥CD于点O,∠1=50°,∠BOF=100°.求证:OD平分∠AOF.
解:∵OE⊥CD,∴∠DOE=90°.
∵∠1=50°,∴∠AOD=40°.
∵∠BOF=100°,∴∠AOF=80°,
∴∠DOF=∠AOF-∠AOD=40°,
∴∠DOF=∠AOD,∴OD平分∠AOF.
18.比较3和26+12的大小,并写出推理过程.
解:因为25<26,所以25+1<26+1,
所以25+12<26+12,所以3<26+12.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,CE⊥DG,垂足为C,∠BAF=50°,∠ACE=140°.试判断CD和AB的位置关系,并说明理由.
解:CD∥AB.
理由:∵CE⊥DG,∴∠ECG=90°.
∵∠ACE=140°,
∴∠ACG=∠ACE-∠ECG=50°.
∵∠BAF=50°,∴∠BAF=∠ACG,
∴CD∥AB.
20.规定:当m,n都是实数,且满足2m=8+n时,就称Pm-1,n+22为“爱心点”.
(1)判断A(5,3),B(4,8)是否为“爱心点”,并说明理由.
(2)若M(a,2a-1)是“爱心点”,请判断点M在第几象限?并说明理由.
解:(1)①m-1=5,n+22=3,解得m=6,n=4,
∴2m=12,8+n=12,∴2m=8+n,
∴A(5,3)是“爱心点”;
②m-1=4,n+22=8,解得m=5,n=14,
显然2m≠8+n,∴B(4,8)不是“爱心点”.
(2)点M在第三象限.
理由:∵M(a,2a-1)是“爱心点”,
∴m-1=a,n+22=2a-1,解得m=a+1,n=4a-4,
代入2m=8+n,得a=-1,∴2a-1=-3,
∴点M的坐标为(-1,-3),即点M在第三象限.
六、(满分12分)
21.如图,方格纸中每个小方格都是边长为1的正方形,四边形ABCD的顶点与点E都是格点,已知点E的坐标为(1,5).
(1)建立适当的平面直角坐标系,并写出四边形ABCD各顶点的坐标.
(2)若把四边形ABCD向上平移2个单位长度,再向右平移2个单位长度,得到四边形A'B'C'D'.请在图中画出四边形A'B'C'D',并写出四边形A'B'C'D'各顶点的坐标.
(3)求四边形ABCD的面积.
解:(1)平面直角坐标系如图所示;点A的坐标为(0,2),点B的坐标为(-2,0),点C的坐标为(0,-1),点D的坐标为(4,0).
(2)四边形A'B'C'D'如图所示;点A'的坐标为(2,4),点B'的坐标为(0,2),点C'的坐标为(2,1),点D'的坐标为(6,2).
(3)四边形ABCD面积为12×6×2+12×6×1=9.
七、(满分12分)
22.如图,在平面直角坐标系中,已知点A的坐标为(a,0),点C的坐标为(b,2),且a,b满足2+a+(b-2)2=0,过点C作CB⊥x轴于点B.
(1)求A,B两点的坐标;
(2)过点B作BD∥AC,交y轴于点D,∠CAB的平分线与∠ODB的平分线相交于点E,求∠AED的度数.
解:(1)∵2+a+(b-2)2=0,
∴2+a=0,b-2=0,解得a=-2,b=2,
∴点A的坐标为(-2,0),点C的坐标为(2,2).
又∵CB⊥x轴,∴点B与点C的横坐标相等,
∴点B的坐标为(2,0).
(2)连接AD.∵BD∥AC,∴∠CAB=∠OBD.
∵∠BOD=90°,∴∠ODB+∠OBD=90°,∴∠ODB+∠CAB=90°.
∵AE,DE分别平分∠CAB,∠ODB,
∴∠OAE+∠ODE=12(∠CAB+∠ODB)=45°.
由题知∠OAD+∠ADO=90°,
∴∠DAE+∠ADE=∠OAE+∠OAD+∠ADO+∠ODE=135°,
∴∠AED=180°-∠DAE-∠ADE=45°.
八、(满分14分)
23.(1)如图1,AB∥CD,∠AEP=40°,∠PFD=130°,求∠EPF的度数.
(2)如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由.
(3)如图3,在(2)的条件下,已知∠P=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数是 12α 接写出答案,不需要写出过程)
解:(1)过点P作PM∥AB(点M在点P的右侧),
∴∠EPM=∠AEP=40°.
∵AB∥CD,∴PM∥CD,∴∠MPF+∠PFD=180°.
∵∠PFD=130°,∴∠MPF=50°,
∴∠EPF=∠EPM+∠MPF=40°+50°=90°.
(2)∠PFC=∠PEA+∠EPF.
理由:过点P作PN∥AB(点N在点P的右侧),
∴∠PEA=∠NPE.
∵AB∥CD,PN∥CD,∴∠FPN=∠PFC,
∴∠PFC=∠NPE+∠EPF=∠PEA+∠EPF.
(3)提示:令AB与PF交点为O,连接EF.由(2)知∠PFC=∠PEA+∠P,∴∠PFE+∠AEF=180°-∠P-∠PEA.∵GE平分∠PEA,FG平分∠PFC,∴∠AEG=12∠PEA,∠PFG=12∠PFC,∴∠G=180°-∠GFE-∠GEF=180°-∠PFE-∠AEF-∠AEG-∠PFG=∠P+∠PEA-12∠PEA-12∠PFC=∠P+12∠PEA-12(∠PEA+∠P)=12∠P=12α.