

2021年北京市门头沟区中考数学一模试卷
展开2021年北京市门头沟区中考数学一模试卷
一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个
1.(2分)如图,在△ABC中,BC边上的高是( )
A.CD B.AE C.AF D.AH
2.(2分)根据国家卫健委官网统计,截至2021年4月10日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗16447.1万剂次,将16447.1万用科学记数法表示为( )
A.1.64471×104 B.1.64471×108
C.1.64471×109 D.1.64471×1010
3.(2分)在下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.平行四边形
C.等腰梯形 D.圆
4.(2分)某个几何体的展开图如图所示,该几何体是( )
A.三棱柱 B.三棱锥 C.长方体 D.圆柱
5.(2分)内角和与外角和相等的图形是( )
A.三角形 B.四边形 C.五边形 D.六边形
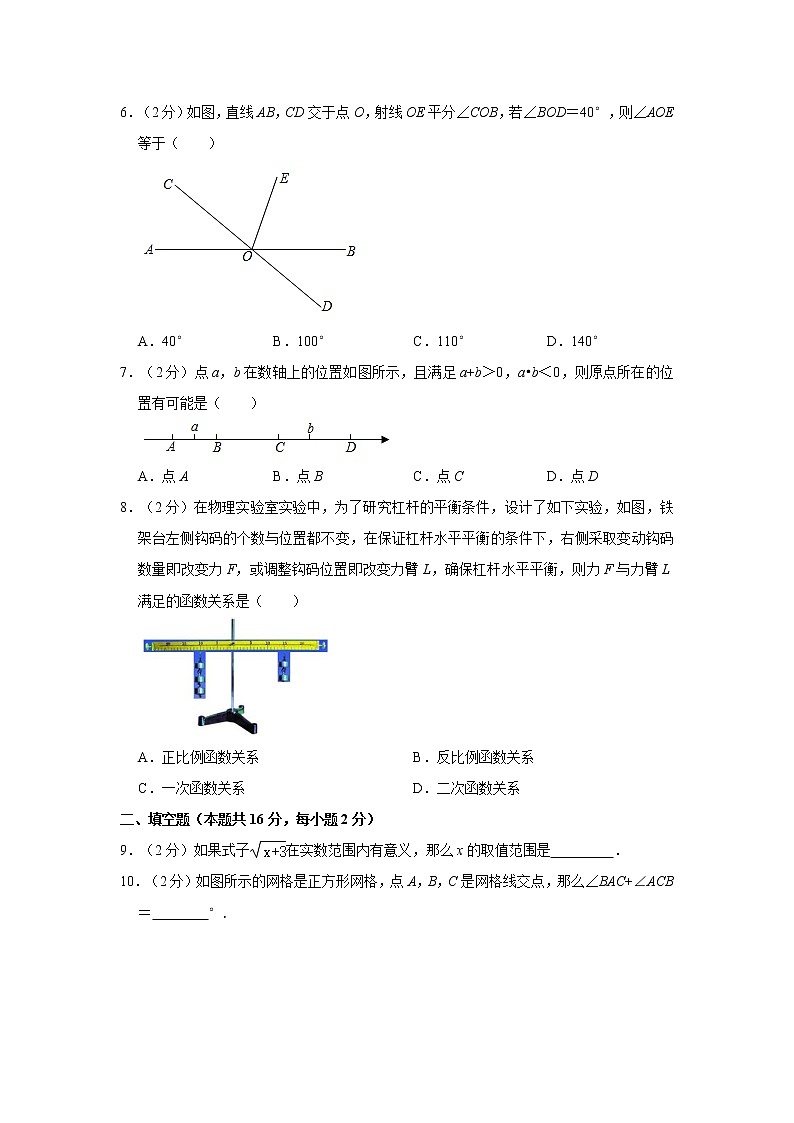
6.(2分)如图,直线AB,CD交于点O,射线OE平分∠COB,若∠BOD=40°,则∠AOE等于( )
A.40° B.100° C.110° D.140°
7.(2分)点a,b在数轴上的位置如图所示,且满足a+b>0,a•b<0,则原点所在的位置有可能是( )
A.点A B.点B C.点C D.点D
8.(2分)在物理实验室实验中,为了研究杠杆的平衡条件,设计了如下实验,如图,铁架台左侧钩码的个数与位置都不变,在保证杠杆水平平衡的条件下,右侧采取变动钩码数量即改变力F,或调整钩码位置即改变力臂L,确保杠杆水平平衡,则力F与力臂L满足的函数关系是( )
A.正比例函数关系 B.反比例函数关系
C.一次函数关系 D.二次函数关系
二、填空题(本题共16分,每小题2分)
9.(2分)如果式子在实数范围内有意义,那么x的取值范围是 .
10.(2分)如图所示的网格是正方形网格,点A,B,C是网格线交点,那么∠BAC+∠ACB= °.
11.(2分)请你写出一个大于2小于3的无理数是 .
12.(2分)已知x+y=﹣1且|x|>1,写出一组符合条件的值 .
13.(2分)已知一元二次方程ax2﹣x+1=0(a≠0),有两个实数根,则a的取值范围是 .
14.(2分)如图,在⊙O中,=,AB=8,半径r=5,则DC= .
15.(2分)下面是某小区随机抽取的100户家庭的月用电量情况统计表:
月户用电量x(千瓦时/户/月)
x≤240
240<x≤300
300<x≤350
350<x≤400
>400
户数(户)
5
22
27
31
15
从中任意抽出一个家庭进行用电情况调查,则抽到的家庭月用电量为第二档(用电量大于240小于等于400为第二档)的概率为 .
16.(2分)以下是小亮的妈妈做晚饭的食材准备及加工时间列表,有一个炒菜锅,一个电饭煲,一个煲汤锅,两个燃气灶可用,做好这顿晚餐一般情况下至少需要 分钟.
用时
种类
准备时间(分钟)
加工时间(分钟)
米饭
3
30
炒菜1
5
6
炒菜2
5
8
汤
5
15
三、解答题(本题共68分,第17~21题每小题5分,第22~24题每小题5分,第25题5分,第26题6分,第27~28题每小题5分)解答应写出文字说明、证明过程或演算步骤。
17.(5分)计算:.
18.(5分)解不等式组:.
19.(5分)已知,如图,△ABC是等边三角形,BD⊥AC于D,E是BC延长线上的一点,DB=DE.求∠E的度数.
20.(5分)已知x2+4x﹣1=0,求代数式(x+2)2﹣(x+3)(x﹣3)+x2的值.
21.(5分)已知:△ABC,CD平分∠ACB.
求作:菱形DFCE,使点F在BC边上点E在AC边上,下面是尺规作图过程作法:①分别以C、D为圆心,大于CD为半径作弧,两弧分别交于点M、N;
②作直线MN分别与AC、BC交于点E、F;
③连接DE、DF,DC与EF的交点记为点G;四边形DFCE为所求作的菱形.
(1)利用直尺和圆规依做法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵DE=EC,DF=FC,
∴EF为DC的垂直平分线.
∵DE=EC,
∴∠EDC=∠ECD.
∵CD平分∠ACB,
∴∠ECD=∠DCB.
∴∠EDC=∠DCB.
∴ ∥ ( )(填推理依据).
同理可证DF∥CE,
∴四边形DFCE为平行四边形.
又∵ ,
∴四边形DFCE为菱形.
22.(6分)已知:如图,在菱形ABCD中,BE⊥AD于点E,延长AD至F,使DF=AE,连接CF.
(1)求证:四边形EBCF是矩形;
(2)若sin∠A=,CF=3,求AF的长.
23.(6分)在平面直角坐标系xOy中,正比例函数y=x与反比例函数y=(k≠0,x≠0)的图象相交于点P(1,1).
(1)求k的值;
(2)过点M(0,a)平行于x轴的直线,分别与第一象限内的正比例函数y=x、反比例函数y=的图象相交于A(x1,y1)、B(x2,y2)当≤a≤2时,求x1+x2的取值范围.
24.(6分)如图,AB是⊙O的直径,C是⊙O上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F,FD上有一点E,CE=EF.
(1)求证:CE是⊙O的切线;
(2)如果sinF=,EF=1,求AB的长.
25.(5分)2021年是中国共产党成立100周年某中学面向学校全体师生征集“礼赞百年”活动作品,作品类别包括征文、书法、绘画.该中学学生小明统计了学校30个教学班上交活动作品的数量(单位:份),相关信息如下:
a.小明所在中学30个教学班上交作品的数量统计图:
b.小明所在中学各班学生上交作品数量的平均数如表:
班级
初一年级(10个班)
初二年级(10个班)
初三年级(10个班)
平均数
110
80
40
(1)该中学各班学生上交作品数量的平均数约为 (结果取整数);
(2)已知该中学全体教师上交作品的数量恰好是该校各班级中,上交作品数量最多的班级与最少的班级的数量差,则全体教师上交作品的数量为 份.
(3)记该中学初一年级学生上交作品数量的方差为s12,初二年级学生上交作品数量的方差为s22,初三年级学生上交作品数量的方差为s32.直接写出s12,s22,s32的大小关系.
26.(6分)在平面直角坐标系xOy中,已知关于x的二次函数y=x2﹣2tx+1.
(1)求该二次函数的对称轴;
(2)若点M(t﹣2,m),N(t+3,n)在抛物线y=x2﹣2x+1上,试比较m、n的大小;
(3)P(x1,y1),Q(x2,y2)是抛物线y=x2﹣2tx+1上的任意两点,若对于﹣1≤x1<3且x2=3,都有y1≤y2,求t的取值范围.
27.(7分)在正方形ABCD中,将边AD绕点A逆时针旋转α(0°<α<90°)得到线段AE,AE与CD延长线相交于点F,过B作BG∥AF交CF于点G,连接BE.
(1)如图1,求证:∠BGC=2∠AEB;
(2)当(45°<α<90°)时,依题意补全图2,用等式表示线段AH,EF,DG之间的数量关系,并证明.
28.(7分)在平面直角坐标系xOy中,⊙O的半径为1,点A是平面内一点,过点A的直线交⊙O于点B和点C(AB≤AC),0≤BC≤1,我们把点B称为点A关于⊙O的“斜射点”.
(1)如图,在点A1(﹣1,1),A2(0,),A3(,0)中,存在关于⊙O的“斜射点”的是 .
(2)已知若A(0,2),点A关于⊙O的斜射点”为点B,则点B的坐标可以是 .(写出两个即可)
(3)若点A直线y=kx+k上,点A关于⊙O的“斜射点”为B(﹣1,0),画出示意图,直接写出k的取值范围.
2021年北京市门头沟区中考数学一模试卷
参考答案与试题解析
一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个
1.(2分)如图,在△ABC中,BC边上的高是( )
A.CD B.AE C.AF D.AH
【分析】根据三角形的高的概念解答.
【解答】解:∵AF⊥BC,
∴BC边上的高是AF,
故选:C.
2.(2分)根据国家卫健委官网统计,截至2021年4月10日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗16447.1万剂次,将16447.1万用科学记数法表示为( )
A.1.64471×104 B.1.64471×108
C.1.64471×109 D.1.64471×1010
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:16447.1万=1.64471×108.
故选:B.
3.(2分)在下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.平行四边形
C.等腰梯形 D.圆
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、是轴对称图形,不是中心对称图形.故此选项错误;
B、是轴对称图形,不是中心对称图形.故此选项错误;
C、是轴对称图形,不是中心对称图形.故此选项错误;
D、是轴对称图形,也是中心对称图形.故此选项正确.
故选:D.
4.(2分)某个几何体的展开图如图所示,该几何体是( )
A.三棱柱 B.三棱锥 C.长方体 D.圆柱
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:三个长方形和两个等腰三角形折叠后,能围成的几何体是三棱柱.
故选:A.
5.(2分)内角和与外角和相等的图形是( )
A.三角形 B.四边形 C.五边形 D.六边形
【分析】任何多边形的外角和是360度,因而这个多边形的内角和是360度.n边形的内角和是(n﹣2)•180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,解方程就可以求出多边形的边数.
【解答】解:设多边形的边数为n,根据题意
(n﹣2)•180°=360°,
解得n=4.
故选:B.
6.(2分)如图,直线AB,CD交于点O,射线OE平分∠COB,若∠BOD=40°,则∠AOE等于( )
A.40° B.100° C.110° D.140°
【分析】由对顶角的性质和平角的定义得到∠AOC=40°,∠BOC=140°,由角平分线的定义得到∠COE=70°,根据角的和差即可求得∠AOE.
【解答】解:∵∠BOD=40°,
∴∠AOC=∠BOD=40°,∠BOC=180°﹣∠BOD=140°,
∴∠COE=∠BOC=×140°=70°,
∴∠AOE=∠AOC+∠COE=40°+70°=110°,
故选:C.
7.(2分)点a,b在数轴上的位置如图所示,且满足a+b>0,a•b<0,则原点所在的位置有可能是( )
A.点A B.点B C.点C D.点D
【分析】先确定a,b的正负情况,再根据数轴上原点与正负数的位置关系确定原点的可能位置.
【解答】解:∵a•b<0,且数轴上a在b的左侧,
∴a<0,b>0,
∵a+b>0,
∴|a|<|b|,即a离原点的距离小于b离原点的距离,
∴点B可能是原点,
故选:B.
8.(2分)在物理实验室实验中,为了研究杠杆的平衡条件,设计了如下实验,如图,铁架台左侧钩码的个数与位置都不变,在保证杠杆水平平衡的条件下,右侧采取变动钩码数量即改变力F,或调整钩码位置即改变力臂L,确保杠杆水平平衡,则力F与力臂L满足的函数关系是( )
A.正比例函数关系 B.反比例函数关系
C.一次函数关系 D.二次函数关系
【分析】根据动力乘以动力臂等于阻力乘以阻力臂即可得到结论.
【解答】解:∵确保杠杆水平平衡,
∴力F与力臂L满足的函数关系是反比例函数关系,
故选:B.
二、填空题(本题共16分,每小题2分)
9.(2分)如果式子在实数范围内有意义,那么x的取值范围是 x≥﹣3 .
【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.
【解答】解:∵在实数范围内有意义,
∴x+3≥0,
解得x≥﹣3.
故答案为:x≥﹣3.
10.(2分)如图所示的网格是正方形网格,点A,B,C是网格线交点,那么∠BAC+∠ACB= 135 °.
【分析】根据勾股定理求出AB,根据勾股定理的逆定理求出∠AOB=90°,求出∠DAC+∠DCA=90°,再求出答案即可.
【解答】解:设小正方形的边长是1,则AO=BO=3,
∵AB==3,
∴△AOB是等腰直角三角形,
∴∠OAB=∠OBA=45°,
∵∠ADC=90°,
∴∠DAC+∠DCA=90°,
∴∠BAC+∠ACB=180°﹣∠OAB﹣∠DAC+90°﹣∠DCA
=180°+90°﹣45°﹣90°
=135°,
故答案为:135.
11.(2分)请你写出一个大于2小于3的无理数是 等 .
【分析】根据算术平方根的性质可以把2和3写成带根号的形式,再进一步写出一个被开方数介于两者之间的数即可.
【解答】解:∵2=,3=,
∴写出一个大于2小于3的无理数是等.
故答案为等.本题答案不唯一.
12.(2分)已知x+y=﹣1且|x|>1,写出一组符合条件的值 .
【分析】根据绝对值的意义,求出x的取值范围,然后根据方程解答即可.
【解答】解:∵|x|>1,
∴x<﹣1或x>1,
取x=﹣2,则x+y=﹣1,
∴y=1
∴
故答案为:.
13.(2分)已知一元二次方程ax2﹣x+1=0(a≠0),有两个实数根,则a的取值范围是 a≤且a≠0 .
【分析】由关于x的一元二次方程ax2﹣x+1=0有两个实数根,即可得判别式△≥0且a≠0,继而可求得a的取值范围.
【解答】解:∵关于x的一元二次方程ax2﹣x+1=0有两个实数根,
∴△=b2﹣4ac=(﹣1)2﹣4×a×1=1﹣4a≥0,
解得:a≤,
∴a的取值范围是a≤且a≠0.
故答案为:a≤且a≠0.
14.(2分)如图,在⊙O中,=,AB=8,半径r=5,则DC= 2 .
【分析】由垂径定理得OC⊥AB,AD=BD=AB=4,再由勾股定理求出OD=3,即可求解.
【解答】解:连接OA,如图所示:
∵,AB=8,
∴OC⊥AB,AD=BD=AB=4,
∴∠ADO=90°,
在Rt△OAD中,由勾股定理得:OD===3,
∴DC=OC﹣OD=5﹣3=2,
故答案为:2.
15.(2分)下面是某小区随机抽取的100户家庭的月用电量情况统计表:
月户用电量x(千瓦时/户/月)
x≤240
240<x≤300
300<x≤350
350<x≤400
>400
户数(户)
5
22
27
31
15
从中任意抽出一个家庭进行用电情况调查,则抽到的家庭月用电量为第二档(用电量大于240小于等于400为第二档)的概率为 .
【分析】根据随机事件概率大小的求法,找准两点:
①符合条件的情况数目;
②全部情况的总数.
二者的比值就是其发生的概率的大小.
【解答】解:∵100户家庭中,用电量大于240小于等于400有22+27+31=80户,
∴抽到的家庭月用电量为第二档(用电量大于240小于等于400为第二档)的概率为=,
故答案为:.
16.(2分)以下是小亮的妈妈做晚饭的食材准备及加工时间列表,有一个炒菜锅,一个电饭煲,一个煲汤锅,两个燃气灶可用,做好这顿晚餐一般情况下至少需要 33 分钟.
用时
种类
准备时间(分钟)
加工时间(分钟)
米饭
3
30
炒菜1
5
6
炒菜2
5
8
汤
5
15
【分析】由题意可知,熬饭准备时间需3分钟,熬饭需要30钟,妈妈可在等待饭熟的这30分钟内先完成煲汤和炒菜,所以妈妈做这顿饭至少需要3+30=33分钟.
【解答】解:3+30=33(分钟),
答:妈妈做晚饭最少要用33分钟,
故答案为:33.
三、解答题(本题共68分,第17~21题每小题5分,第22~24题每小题5分,第25题5分,第26题6分,第27~28题每小题5分)解答应写出文字说明、证明过程或演算步骤。
17.(5分)计算:.
【分析】直接利用绝对值的性质以及零指数幂的性质和特殊角的三角函数值、负整数指数幂的性质分别化简得出答案.
【解答】解:原式=﹣1﹣2×+2
=﹣1﹣+2
=1.
18.(5分)解不等式组:.
【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:解不等式2x﹣1>3(x﹣1),得x<2,
解不等式<x+3,得x>﹣,
则不等式组的解集为﹣<x<2.
19.(5分)已知,如图,△ABC是等边三角形,BD⊥AC于D,E是BC延长线上的一点,DB=DE.求∠E的度数.
【分析】根据等边三角形的性质得出AB=BC,∠ABC=60°,根据“三线合一”得出∠DBC=∠ABD=30°,根据等腰三角形的性质得出即可.
【解答】解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=60°,
∵BD⊥AC,
∴∠DBC=∠ABD==30°,
∵DB=DE,
∴∠E=∠DBC=30°.
20.(5分)已知x2+4x﹣1=0,求代数式(x+2)2﹣(x+3)(x﹣3)+x2的值.
【分析】先根据完全平方公式和平方差公式展开,再合并同类项即可化简原式,继而根据已知等式得出x2+4x=1,代入计算即可.
【解答】解:原式=x2+4x+4﹣x2+9+x2
=x2+4x+13,
∵x2+4x﹣1=0,
∴x2+4x=1,
则原式=1+13=14.
21.(5分)已知:△ABC,CD平分∠ACB.
求作:菱形DFCE,使点F在BC边上点E在AC边上,下面是尺规作图过程作法:①分别以C、D为圆心,大于CD为半径作弧,两弧分别交于点M、N;
②作直线MN分别与AC、BC交于点E、F;
③连接DE、DF,DC与EF的交点记为点G;四边形DFCE为所求作的菱形.
(1)利用直尺和圆规依做法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵DE=EC,DF=FC,
∴EF为DC的垂直平分线.
∵DE=EC,
∴∠EDC=∠ECD.
∵CD平分∠ACB,
∴∠ECD=∠DCB.
∴∠EDC=∠DCB.
∴ DE ∥ CF ( 内错角相等两直线平行 )(填推理依据).
同理可证DF∥CE,
∴四边形DFCE为平行四边形.
又∵ ED=EC ,
∴四边形DFCE为菱形.
【分析】(1)根据几何语言画出对应的几何图形;
(2)先证明DE∥CF,DF∥CE,则可判断四边形DFCE为平行四边形,然后利用ED=EC得到四边形DFCE为菱形.
【解答】(1)解:如图,四边形DFCE为所求作;
(2)证明:∵DE=EC,DF=FC,
∴EF为DC的垂直平分线.
∵DE=EC,
∴∠EDC=∠ECD.
∵CD平分∠ACB,
∴∠ECD=∠DCB.
∴∠EDC=∠DCB.
∴DE∥CF(内错角相等两直线平行),
同理可证DF∥CE,
∴四边形DFCE为平行四边形.
又∵ED=EC,
∴四边形DFCE为菱形.
故意答案为DE,CF,内错角相等两直线平行;ED=EC.
22.(6分)已知:如图,在菱形ABCD中,BE⊥AD于点E,延长AD至F,使DF=AE,连接CF.
(1)求证:四边形EBCF是矩形;
(2)若sin∠A=,CF=3,求AF的长.
【分析】(1)由菱形的性质得出AD=BC,AD∥BC,求出EF=BC,再由平行四边形的判定得出四边形EBCF是平行四边形,然后由矩形的判定即可得出结论;
(2)由菱形的性质得AB=BC,再由矩形的性质得EF=BC,BE=CF=3,然后由锐角三角函数定义得AB=5,则EF=BC=AB=5,由勾股定理求出AE=4,即可求解.
【解答】(1)证明:∵四边形ABCD菱形,
∴AD=BC,AD∥BC,
又∵DF=AE,
∴DF+DE=AE+DE,
即:EF=AD,
∴EF=BC,
∴四边形EBCF是平行四边形,
又∵BE⊥AD,
∴∠BEF=90°.
∴四边形EBCF是矩形;
(2)解:∵四边形ABCD菱形,
∴AB=BC,
∵四边形EBCF是矩形,
∴EF=BC,BE=CF=3,
∵BE⊥AD,
∴∠AEB=90°,
∵sin∠A==,BE=3,
∴AB=5,
∴EF=BC=AB=5,AE===4,
∴AF=AE+EF=4+5=9.
23.(6分)在平面直角坐标系xOy中,正比例函数y=x与反比例函数y=(k≠0,x≠0)的图象相交于点P(1,1).
(1)求k的值;
(2)过点M(0,a)平行于x轴的直线,分别与第一象限内的正比例函数y=x、反比例函数y=的图象相交于A(x1,y1)、B(x2,y2)当≤a≤2时,求x1+x2的取值范围.
【分析】(1)运用待定系数法将点P(1,1)代入y=(k≠0,x≠0),求出k即可;
(2)由题意得:y1=y2=a,进而可得x1+x2=a+,根据a2+b2≥2ab,即可求出x1+x2≥2,再由≤a≤2,即可得出结论.
【解答】解:(1)∵反比例函数y=(k≠0,x≠0)的图象经过点P(1,1),
∴1=,
∴k=1,
(2)由题意得:y1=y2=a,
∴x1=y1=a,x2==,
∴x1+x2=a+,
∵a>0,
∴a+≥2=2,
∴x1+x2≥2,
当a=时,M(0,),A(,),B(2,),
∴x1+x2=+2=,
当a=2,M(0,2),A(2,2),B(,2),
∴x1+x2=2+=,
∴x1+x2的取值范围为:2≤x1+x2≤.
24.(6分)如图,AB是⊙O的直径,C是⊙O上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F,FD上有一点E,CE=EF.
(1)求证:CE是⊙O的切线;
(2)如果sinF=,EF=1,求AB的长.
【分析】(1)连接OC,由FD⊥AB得到∠1+∠F=90°,由等腰三角形的性质得到∠3=∠F,∠1=∠2,进而得到∠2+∠3=90°,即∠ECO=90°,由切线的判定可得CE是⊙O的切线;
(2)根据三角函数,设出AD=3k,AF=5k,可得FD=4k,连接CB交FD于点G,由AB为⊙O直径,得到∠ACB=∠FCB=90°,推出∠F=∠B,再根据边角关系得出结论.
【解答】(1)证明:如图1,连接OC,
∵FD⊥AB,
∴∠1+∠F=90°,
∵CE=EF,OA=OC,
∴∠3=∠F,∠1=∠2,
∴∠2+∠3=90°,
∴∠ECO=90°,
∴OC⊥CE,
∵OC是⊙O的半径,
∴CE是⊙O的切线;
(2)解:如图2
∵FD⊥AB,sin∠F=,
设AD=3k,AF=5k,可得FD=4k,
∵D为OB中点,
∴OD=DB=OB=OA=AD,
∴DB=k,
连接CB交FD于点G,
∵AB为⊙O直径,
∴∠ACB=∠FCB=90°,
∴∠F=∠B,
∵DB=k,
∴GD=k,可得FG=k,
∵∠FCB=90°,
∴∠5+∠F=∠3+∠4,
∵∠F=∠3,
∴∠4=∠5,
∴CE=EF=EG,
∵EF=1,
∴FG=2,
∴=2,k=,
∴AB=4k=.
25.(5分)2021年是中国共产党成立100周年某中学面向学校全体师生征集“礼赞百年”活动作品,作品类别包括征文、书法、绘画.该中学学生小明统计了学校30个教学班上交活动作品的数量(单位:份),相关信息如下:
a.小明所在中学30个教学班上交作品的数量统计图:
b.小明所在中学各班学生上交作品数量的平均数如表:
班级
初一年级(10个班)
初二年级(10个班)
初三年级(10个班)
平均数
110
80
40
(1)该中学各班学生上交作品数量的平均数约为 77 (结果取整数);
(2)已知该中学全体教师上交作品的数量恰好是该校各班级中,上交作品数量最多的班级与最少的班级的数量差,则全体教师上交作品的数量为 130 份.
(3)记该中学初一年级学生上交作品数量的方差为s12,初二年级学生上交作品数量的方差为s22,初三年级学生上交作品数量的方差为s32.直接写出s12,s22,s32的大小关系.
【分析】(1)利用加权平均数公式求该中学各班学生上交作品数量的平均数即可;
(2)从统计图中找出上交作品数量最多的班级是初一年级6班140份,找出最少的班级是初三年级10班10份,全体教师上交作品的数量=140﹣10=130份;
(3)先求出初一年级学生上交作品数量的方差为=420,初二年级学生上交作品数量的方差为==100,初三年级学生上交作品数量的方差为=250,再比较大小即可.
【解答】解:(1)该中学各班学生上交作品数量的平均数为:
=≈77(份),
故答案为:77.
(2)上交作品数量最多的班级是初一年级6班140份,最少的班级是初三年级10班10份,
全体教师上交作品的数量=140﹣10=130份,
故答案为:130;
(3)初一年级学生上交作品数量的方差为:
=(202+102+202+202+302+302+0+102+302+102)=420,
初二年级学生上交作品数量的方差为:
=(102+02+102+102+02+202+0+102+102+102)=100,
初三年级学生上交作品数量的方差为:
=(202+302+102+102+02+202+0+102+102+202)=250,
∵420>250>100,
∴>>.
26.(6分)在平面直角坐标系xOy中,已知关于x的二次函数y=x2﹣2tx+1.
(1)求该二次函数的对称轴;
(2)若点M(t﹣2,m),N(t+3,n)在抛物线y=x2﹣2x+1上,试比较m、n的大小;
(3)P(x1,y1),Q(x2,y2)是抛物线y=x2﹣2tx+1上的任意两点,若对于﹣1≤x1<3且x2=3,都有y1≤y2,求t的取值范围.
【分析】(1)把解析式化成顶点式即可求得;
(2)根据二次函数的性质即可判断;
(3)当t≤1时,此时﹣1≤x1<3,x2=3都有y1≤y2,当t>1时,令x1=﹣1时,y1>y2,不符合题意,由此即可解决问题.
【解答】解:(1)∵y=x2﹣2tx+2=(x﹣t)2﹣t2+2
∴抛物线的对称轴为直线x=t;
(2)抛物线开口向上,对称轴为直线x=t,
∴点M(t﹣2,m)关于对称轴的对称点为(t+2,m),
t<t+2<t+5,
∴m<n,
故答案为<;
(3)当t≤1时,此时﹣1≤x1<3,x2=3都有y1≤y2,符合题意;
当t>1时,令xx1=﹣1时,y1>y2,不符合题意.
综上所述:t≤1.
27.(7分)在正方形ABCD中,将边AD绕点A逆时针旋转α(0°<α<90°)得到线段AE,AE与CD延长线相交于点F,过B作BG∥AF交CF于点G,连接BE.
(1)如图1,求证:∠BGC=2∠AEB;
(2)当(45°<α<90°)时,依题意补全图2,用等式表示线段AH,EF,DG之间的数量关系,并证明.
【分析】(1)根据BG∥AF,得到∠GBE=∠AEB,由AD绕点A逆时针旋转α得到线段AE,得到AE=AB,∠ABE=∠AEB=∠GBE,由正方形性质得到CD∥AB,得到∠BGC=2∠AEB;
(2)按照题意补全图形即可,在DC上取DN=AH,连接AN交BG于M,交BE于P,连接HM,EM,利用△ADN≌△BAH、△ABP≌△MBP、△ABH≌△MBH证明A、H、M、B共圆,从而可得∠DNA=∠GMN,GN=GM,再证明EF=GM,即可得到EF=AH+DG.
【解答】解:(1)证明:∵边AD绕点A逆时针旋转α(0°<α<90°)得到线段AE,
∴AD=AE,
∵正方形ABCD,
∴AB=AD=AE,
∴∠AEB=∠ABE,
∵BG∥AF,
∴∠AEB=∠GBE,
∴∠ABE=∠AEB=∠GBE,
∴∠ABG=2∠AEB,
∵正方形ABCD,
∴AB∥CD,
∴∠BGC=∠ABG,
∴∠BGC=2∠AEB;
(2)补全图2如下:
线段AH,EF,DG之间的数量关系为:EF=AH+DG,理由如下:
在DC上取DN=AH,连接AN交BG于M,交BE于P,连接HM,EM,如图:
∵正方形ABCD,
∴AB=AD,∠ADN=∠BAH=90°,
又DN=AH,
∴△ADN≌△BAH(SAS),
∴∠DNA=∠AHB,∠DAN=∠ABH,
∵∠DNA+∠DAN=90°,
∴∠DAN+∠AHB=90°,
∴∠APH=90°,
∴∠BPM=∠BPA=90°,
由(1)知∠ABE=∠GBE,
且BP=BP,
∴△ABP≌△MBP(ASA),
∴AB=MB,
而BH=BH,∠ABE=∠GBE,
∴△ABH≌△MBH(SAS),
∴∠HAB=∠HMB=90°,
∴A、H、M、B共圆,
∴∠AHB=∠AMB=∠GMN,
∴∠DNA=∠GMN,
∴GN=GM,
∵CF∥AB,BG∥AF,
∴四边形ABGF是平行四边形,
∴BG=AF,
∵AF=AD=AB=MB,
∴EF=GM,
∴EF=GN,
∵GN=DG+DN,
∴EF=DG+AH.
28.(7分)在平面直角坐标系xOy中,⊙O的半径为1,点A是平面内一点,过点A的直线交⊙O于点B和点C(AB≤AC),0≤BC≤1,我们把点B称为点A关于⊙O的“斜射点”.
(1)如图,在点A1(﹣1,1),A2(0,),A3(,0)中,存在关于⊙O的“斜射点”的是 A1,A2 .
(2)已知若A(0,2),点A关于⊙O的斜射点”为点B,则点B的坐标可以是 (,),(,) .(写出两个即可)
(3)若点A直线y=kx+k上,点A关于⊙O的“斜射点”为B(﹣1,0),画出示意图,直接写出k的取值范围.
【分析】(1)由图象直接判断点A1存在关于⊙O的“斜射点”;对于点A2,过点A2作弦B2C2⊥y轴,用勾股定理求出弦B2C2的长为1,可得点A2存在关于⊙O的“斜射点”;过点A3作弦B3C3⊥x轴,说明此时弦B3C3的值最小,再用勾股定理求B3C3的长,可得B3C3的值大于1,因此点A3不存在关于⊙O的“斜射点”;
(2)设⊙O交x轴于点C,连接AC交⊙O于点B,先证明点B是点A关于⊙O的“斜射点”,再根据相似三角的性质求出点B的坐标,点B关于y轴的对称点也符合题意;
(3)先证明当直线y=kx+k与x轴成60°角时,BC=1,求出此时k的值,这个值就是k>0时的最小值或k<0时的最大值,由此求出k的取值范围.
【解答】解:(1)如图1,由图象可知,对于⊙O外的任意一点A,都存在点A关于⊙O的“斜射点”,
∵点A1在⊙O外,
∴点A1存在关于⊙O的“斜射点”;
过点A2作弦B2C2与y轴垂直,连接OC2,
则A2C2=A2B2==,
∴B2C2=1,
∴点A2存在关于⊙O的“斜射点”;
过点A3作弦B3C3与x轴垂直,连接OB3,
设点O到弦B3C3的距离为d,
则A3B3==,
当B3C3⊥x轴时,d的值最大,此时A3B3的值最小,B3C3的值也最小;
∵A3B3==,
∴B3C3=,
∴B3C3>1,
∴点A3不存在关于⊙O的“斜射点”.
故答案为:A1,A2.
(2)如图2,设⊙O交x轴于点C,
连接AC交⊙O于点B,作OD⊥AC于点D、BE⊥y轴于点E,
则∠ODC=∠ODB=∠AEB=90°,
∵OA=2,OC=1,∠AOC=90°,
∴AC==,
∴BC=CD=OC•cos∠ACO=1×=,
∴BC=<1,
∴点B是点A关于⊙O的“斜射点”;
∵AB=﹣=,
∴BE=AB•sin∠OAC=1×=;
∵=tan∠OAC=,
∴AE=2BE=2×=,
∴OE=2﹣=,
∴B(,).
同理,点B关于y轴的对称点也符合题意,其坐标为(,).
故答案为:(,),(,).
(3)如图3,当k>0时,直线y=kx+k交y轴于点D(0,k),
当∠OBD=60°时,连接OC,
∵OC=OB,
∴△BOC是等边三角形,
∴BC=OB=1,
此时,点B是点A关于⊙O的“斜射点”,OD=OB•tan60°=,
∵当OD≥时,BC≤1,
∴k≥;
如图4,当k<0时,同理可得,当k≤时,点B是点A关于⊙O的“斜射点”.
综上所述,k的取值范围是:k≥或k≤.
2023年北京市门头沟区中考数学二模试卷(含解析): 这是一份2023年北京市门头沟区中考数学二模试卷(含解析),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年北京市门头沟区中考数学二模试卷(含解析): 这是一份2023年北京市门头沟区中考数学二模试卷(含解析),共27页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
北京市门头沟区2023届初三中考数学一模试卷+答案: 这是一份北京市门头沟区2023届初三中考数学一模试卷+答案,共15页。试卷主要包含了方程的解为,分解因式等内容,欢迎下载使用。












