贵州省毕节市2020-2021学年八年级下学期期中考试数学试卷（word版 含答案）

这是一份贵州省毕节市2020-2021学年八年级下学期期中考试数学试卷（word版 含答案），共6页。试卷主要包含了请将答案正确填写在答题卡上;等内容，欢迎下载使用。

注意事项：
1．答题前填写好自己的姓名、班级、考号等信息;
2．请将答案正确填写在答题卡上;
卷I（选择题）
一、 选择题 （本题共计 12 小题 ，每题 3 分 ，共计36分 ）
1. 不等式13x<1的解集是( )
A.x<13B.x>13C.x>3D.x<3
2. 如图，△OAB绕点O逆时针旋转80∘到△OCD的位置，已知∠AOB=45∘，则∠AOD等于( )

A.55∘B.45∘C.40∘D.35∘
3. 如图，△ABC中，∠ACB=90∘，∠B=30∘，AD是∠BAC的平分线，DE⊥AB于E，AD，CE相交于点H，则图中的等腰三角形有( )

A.2个B.3个C.4个D.5个
4. a的3倍与3的和不大于1，用不等式表示正确的是( )
A.3a+3<1B.3a+3≤1C.3a-3≥1D.3a+3≥1
5. 在把a2x+ay-a2xy分解因式时，应提取的公因式是（ ）
A.a2B.aC.axD.ay
6. 一个三角形任意一边上的高都是这边上的中线，则对这个三角形最准确的判断是( )
A.等腰三角形B.直角三角形
C.正三角形D.等腰直角三角形
7. 某种出租车的收费标准：起步价7元（即行驶距离不超过3千米都需付7元车费），超过3千米后，每增加1千米，加收2.4元（不足1千米按1千米计）．某人乘这种出租车从甲地到乙地共付车费19元，那么甲地到乙地路程的最大值是( )
A.5千米B.7千米C.8千米D.15千米
8. 下列图形中是中心对称图形的是( )
A.B.C.D.
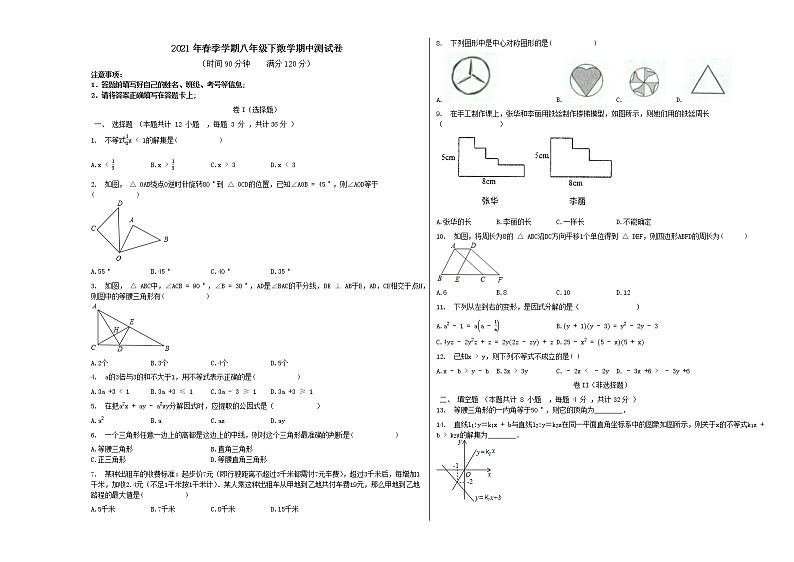
9. 在手工制作课上，张华和李丽用铁丝制作楼梯模型，如图所示，则她们用的铁丝周长（ ）

A.张华的长B.李丽的长C.一样长D.不能确定
10. 如图，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为( )

A.6B.8C.10D.12
11. 下列从左到右的变形，是因式分解的是（ ）
A.a2-1=aa-1aB.y+1y-3=y2-2y-3
C.4yz-2y2z+z=2y2z-zy+zD.25-x2=5-x5+x
12. 已知x>y，则下列不等式不成立的是( )
A.x-b>y-bB.3x>3yC.-2x<-2yD.-3x+6>-3y+6
卷II（非选择题）
二、 填空题 （本题共计 8 小题 ，每题 4 分 ，共计32分 ）
13. 等腰三角形的一内角等于50∘，则它的顶角为________．
14. 直线l1:y＝k1x+b与直线l2:y＝k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b>k2x的解集为________．


在△ABC中，∠A:∠B:∠C=1:2:3，AB=6cm，则BC=________cm．
16. 将一块直尺与一块三角板如图所示放置，若∠1=40∘，则∠2的度数为________．


17. 等腰三角形一腰上的高与另一腰的夹角为36∘，那么这个等腰三角形的底角为________．
18. 如图，在△ABC中，AB=2，BC=3.6，∠B=60∘，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为________．

19. 不等式组x+2≥0,2x-420. 分解因式：3x2+6x=________.
三、 解答题 （本题共计 5 题 ，共计52分 ）
21. 解不等式组5+2x≥3x+13>x2 ，并写出不等式组的整数解． （本题10分 ）
22. 如图所示，三角形ABC中，任意一点P(a, b)经平移后对应点P1(a-2, b+3)，将△ABC作同样的平移得

到△A1B1C1．求A1，B1，C1的坐标．并画出△A1B1C1 （本题10分 ）
△ABC为正三角形，点M是BC上任意一点，点N是CA上任意一点，且BM=CN，BN与AM相交于Q点，∠AQN等于多少度？ （本题10分 ）


24. 如图，点E，F在线段BD上，已知AF⊥BD，CE⊥BD，AD=CB，DE=BF.求证：∠B=∠D .
（本题10分 ）

某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表：

若工厂计划获利14万元，问A，B两种产品应分别生产多少件？（本题4分 ）


(2)若工厂投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？（本题4分 ）

(3)在(2)条件下，哪种方案获利最大？并求最大利润．（本题4分 ）
参考答案与试题解析
2021年春季学期八年级下数学期中测试卷
一、 选择题 （本题共计 12 小题 ，每题 3 分 ，共计36分 ）
1.
【答案】
D
【解答】
解：不等式13x<1两边同乘以三可得：
x<3.
故选D.
2.
【答案】
D
【解答】
解：根据旋转的性质可知，D和B为对应点，∠DOB为旋转角，即∠DOB=80∘，
所以∠AOD=∠DOB-∠AOB=80∘-45∘=35∘．
故选D.
3.
【答案】
C
【解答】
解：∵ ∠ACB=90∘，∠B=30∘，
∴ ∠BAC=60∘，
∵ AD是角平分线，
∴ ∠CAD=∠BAD=30∘，
∴AD=BD．
∴ △ABD是等腰三角形．
∵ AD是角平分线，∠ACB=90∘，DE⊥AB，
∴ CD=ED，E是AB的中点，
∴ AC=AE，CE=BE，
∴ △CDE，△ACE，△CEB是等腰三角形；
∴ 此图中有4个等腰三角形．
故选C.
4.
【答案】
B
【解答】
解：a的3倍与3的和不大于1，用不等式表示为3a+3≤1，
故选B.
5.
【答案】
B
【解答】
解：a2x与ay与a2xy的公因式为a，
故把a2x+ay-a2xy分解因式时应该提取公因式是a．
故选B．
6.
【答案】
C
【解答】
解：根据等腰三角形的三线合一的性质，可得三边相等，
则对这个三角形最准确的判断是正三角形．
故选C．
7.
【答案】
C
【解答】
解：甲地到乙地的路程为x千米，
依题意得：2.4(x-3)≤19-7，
则2.4x-7.2≤12，
即2.4x≤19.2，
∴ x≤8．
因此x的最大值为8．
故选C．
8.
【答案】
C
【解答】
解：轴对称图形两部分沿对称轴折叠后可重合；
中心对称图形旋转180度后与原图形重合．
观察选项可知，A,B,D是轴对称图形，不是中心对称图形，C是中心对称图形.
故选C.
9.
【答案】
C
【解答】
解：因为经过平移两个图形可变为两个边长相等的长方形，所以两人用的一样多．
故选C．
10.
【答案】
C
【解答】
此题暂无解答
11.
【答案】
D
【解答】
解：把一个多项式化成几个整式的乘积形式，这种变形叫做因式分解；
A，没把一个多项式转化成几个整式乘积，含有分式，故A错误；
B，是整式乘法，故B错误；
C，没把一个多项式转化成几个整式乘积，故C错误；
D，把一个多项式转化成几个整式乘积，故D正确．
故选D．
12.
【答案】
D
【解答】
解：A，∵ x>y，∴ x-b>y-b，故本选项成立；
B，∵ x>y，∴ 3x>3y，故本选项成立；
C，∵ x>y，∴ -x<-y，∴ -2x<-2y，故选项成立；
D，∵ x>y，∴ -3x<-3y，∴ -3x+6<-3y+6，故本选项不成立．
故选D．
二、 填空题 （本题共计 8 小题 ，每题 4 分 ，共计32分 ）
13.
【答案】
50∘，80∘或65∘，65∘
【解答】
解：当50∘的角为底角时，只一个底角也为50∘，
顶角=180∘-2×50∘=80∘；
当50∘的角为顶角时，
底角=(180∘-50∘)÷2=65∘．
故答案为：50∘，80∘或65∘，65∘．
14.
【答案】
x<-1
【解答】
能使函数y＝k1x+b的图象在函数y＝k2x的上边时的自变量的取值范围是x<-1．
故关于x的不等式k1x+b>k2x的解集为：x<-1．
15.
【答案】
3
【解答】
解：∵ ∠A+∠B+∠C=180∘，∠A:∠B:∠C=1:2:3，
∴ ∠A=30∘，∠C=90∘，
∵ AB=6cm，
∴ BC=12AB=3cm，
故答案为：3．
16.
【答案】
130∘
【解答】
解：
∵ ∠1=40∘，
∴ ∠3=90∘-∠1=90∘-40∘=50∘，
∴ ∠4=180∘-50∘=130∘，
∵ 直尺的两边互相平行，
∴ ∠2=∠4=130∘．
故答案为：130∘．
17.
【答案】
63∘或27∘
【解答】
解：在三角形ABC中，设AB=AC，BD⊥AC于D．
①若是锐角三角形，∠A=90∘-36∘=54∘，
底角=(180∘-54∘)÷2=63∘；
②若三角形是钝角三角形，∠BAC=36∘+90∘=126∘，
此时底角=(180∘-126∘)÷2=27∘．
所以等腰三角形底角的度数是63∘或27∘．
故答案为：63∘或27∘．
18.
【答案】
1.6
【解答】
解：由旋转的性质可得：AD=AB，
∵ ∠B=60∘，
∴ △ABD是等边三角形，
∴ BD=AB，
∵ AB=2，BC=3.6，
∴ CD=BC-BD=3.6-2=1.6．
故答案为：1.6.
19.
【答案】
6
【解答】
解：不等式组x+2≥0,2x-4所以正整数解为：1，2，3，
所有正整数解的和为：6.
故答案为：6.
20.
【答案】
3x(x+2)
【解答】
解：3x2+6x=3x(x+2).
故答案为：3x(x+2).
三、 解答题 （本题共计 5 小题 ，每题 10 分 ，共计50分 ）
21.
【答案】
5+2x≥3x+13>x2 ，
由①得：x≥-1，
由②得：x<2，
∴ 不等式组的解集为：-1≤x<2，
∴ 不等式组的整数解是：-1，0，1．
【解答】
5+2x≥3x+13>x2 ，
由①得：x≥-1，
由②得：x<2，
∴ 不等式组的解集为：-1≤x<2，
∴ 不等式组的整数解是：-1，0，1．
22.
【答案】
解：∵ 点P(a, b)经平移后对应点P1(a-2, b+3)，
∴ P点向上平移3个单位，向左平移2个单位，
由图知：A(1, 1)，B(-1, -1)，C(4, -2)，
∴ A1，B1，C1的坐标分别为：(-1, 4)，(-3, 2)，(2, 1)．
【解答】
解：∵ 点P(a, b)经平移后对应点P1(a-2, b+3)，
∴ P点向上平移3个单位，向左平移2个单位，
由图知：A(1, 1)，B(-1, -1)，C(4, -2)，
∴ A1，B1，C1的坐标分别为：(-1, 4)，(-3, 2)，(2, 1)．
23.
【答案】
解：∵ △ABC为正三角形，
∴ ∠ABC=∠C=∠BAC=60∘，AB=BC.
在△AMB和△BNC中
AB=BC，∠ABC=∠C，BM=CN，
∴ △AMB≅△BNC(SAS).
∵ ∠ANB=∠C+∠NBC=60∘+∠NBC，
∠MAN=∠BAC-∠MAB=60∘-∠MAB，
又∵ ∠NBC=∠MAB（全等三角形对应角相等），
∴ ∠ANB+∠MAN=120∘.
又∵ ∠ANQ+∠MAN+∠AQN=180∘，
∴ ∠AQN=180∘-∠ANB-∠MAN，
∠AQN=180∘-(∠ANB+∠MAN)，
=180∘-120∘=60∘.
【解答】
解：∵ △ABC为正三角形，
∴ ∠ABC=∠C=∠BAC=60∘，AB=BC.
在△AMB和△BNC中
AB=BC，∠ABC=∠C，BM=CN，
∴ △AMB≅△BNC(SAS).
∵ ∠ANB=∠C+∠NBC=60∘+∠NBC，
∠MAN=∠BAC-∠MAB=60∘-∠MAB，
又∵ ∠NBC=∠MAB（全等三角形对应角相等），
∴ ∠ANB+∠MAN=120∘.
又∵ ∠ANQ+∠MAN+∠AQN=180∘，
∴ ∠AQN=180∘-∠ANB-∠MAN，
∠AQN=180∘-(∠ANB+∠MAN)，
=180∘-120∘=60∘.
24.
【答案】
证明：∵DE=BF，
∴ DE+EF=BF+EF，
∴ DF=BE.
在Rt△ADF和Rt△CBE中，
DF=BE,AD=CB,
∴ Rt△ADF≅Rt△CBE(HL)，
∴ ∠B=∠D．
【解答】
证明：∵DE=BF，
∴ DE+EF=BF+EF，
∴ DF=BE.
在Rt△ADF和Rt△CBE中，
DF=BE,AD=CB,
∴ Rt△ADF≅Rt△CBE(HL)，
∴ ∠B=∠D．
25.
【答案】
解：(1)设A种产品x件，B种为(10-x)件，
x+2(10-x)=14，
解得x=6，
答：A生产6件，B生产4件.
(2)设A种产品x件，B种为(10-x)件，
3x+5(10-x)≤44，x+2(10-x)>14，
解得3≤x<6．
方案一：A生产3件，B生产7件；
方案二：A生产4件，B生产6件；
方案三：A生产5件，B生产5件．
(3)当x=3时，利润为3×1+7×2=17；
当x=4时，利润为4×1+6×2=16；
当x=5时，利润为5×1+5×2=15.
15<16<17，
所以第一种方案获利最大，最大利润是17万元．
【解答】
解：(1)设A种产品x件，B种为(10-x)件，
x+2(10-x)=14，
解得x=6，
答：A生产6件，B生产4件.
(2)设A种产品x件，B种为(10-x)件，
3x+5(10-x)≤44，x+2(10-x)>14，
解得3≤x<6．
方案一：A生产3件，B生产7件；
方案二：A生产4件，B生产6件；
方案三：A生产5件，B生产5件．
(3)当x=3时，利润为3×1+7×2=17；
当x=4时，利润为4×1+6×2=16；
当x=5时，利润为5×1+5×2=15.
15<16<17，
所以第一种方案获利最大，最大利润是17万元．A种产品
B种产品
成本（万元∕件）
3
5
利润（万元∕件）
1
2