
人教版七年级下册第五章 相交线与平行线综合与测试当堂检测题
展开2021年度人教版七年级数学下册《第5章相交线与平行线》章末复习综合训练(附答案)
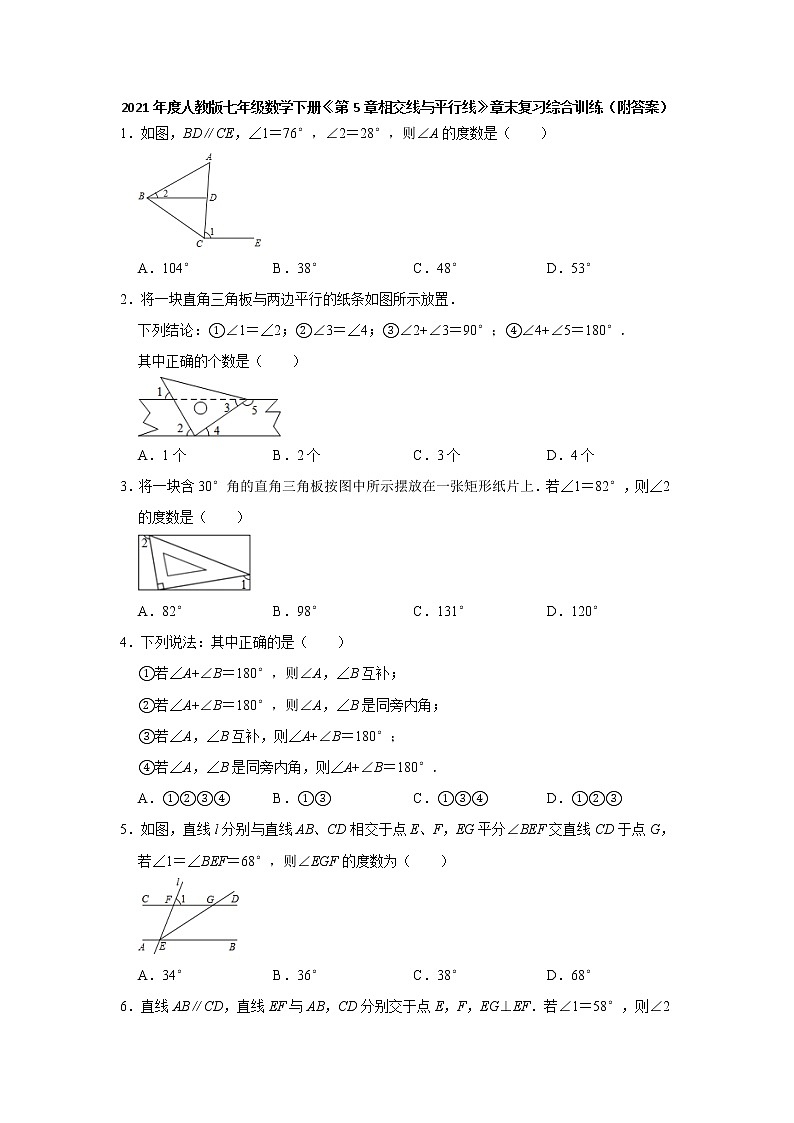
1.如图,BD∥CE,∠1=76°,∠2=28°,则∠A的度数是( )
A.104° B.38° C.48° D.53°
2.将一块直角三角板与两边平行的纸条如图所示放置.
下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠3=90°;④∠4+∠5=180°.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
3.将一块含30°角的直角三角板按图中所示摆放在一张矩形纸片上.若∠1=82°,则∠2的度数是( )
A.82° B.98° C.131° D.120°
4.下列说法:其中正确的是( )
①若∠A+∠B=180°,则∠A,∠B互补;
②若∠A+∠B=180°,则∠A,∠B是同旁内角;
③若∠A,∠B互补,则∠A+∠B=180°;
④若∠A,∠B是同旁内角,则∠A+∠B=180°.
A.①②③④ B.①③ C.①③④ D.①②③
5.如图,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠1=∠BEF=68°,则∠EGF的度数为( )
A.34° B.36° C.38° D.68°
6.直线AB∥CD,直线EF与AB,CD分别交于点E,F,EG⊥EF.若∠1=58°,则∠2的度数为( )
A.18° B.32° C.48° D.62°
7.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,FG平分∠EFD交AB于点G,若∠BEF=70°,则∠AGF的度数为( )
A.35° B.45° C.55° D.65°
8.如图,a∥b,则下列结论中正确的是( )
A.∠1=∠2 B.∠2+∠3=180° C.∠1=∠4 D.∠2=4
9.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80° B.85° C.90° D.95°
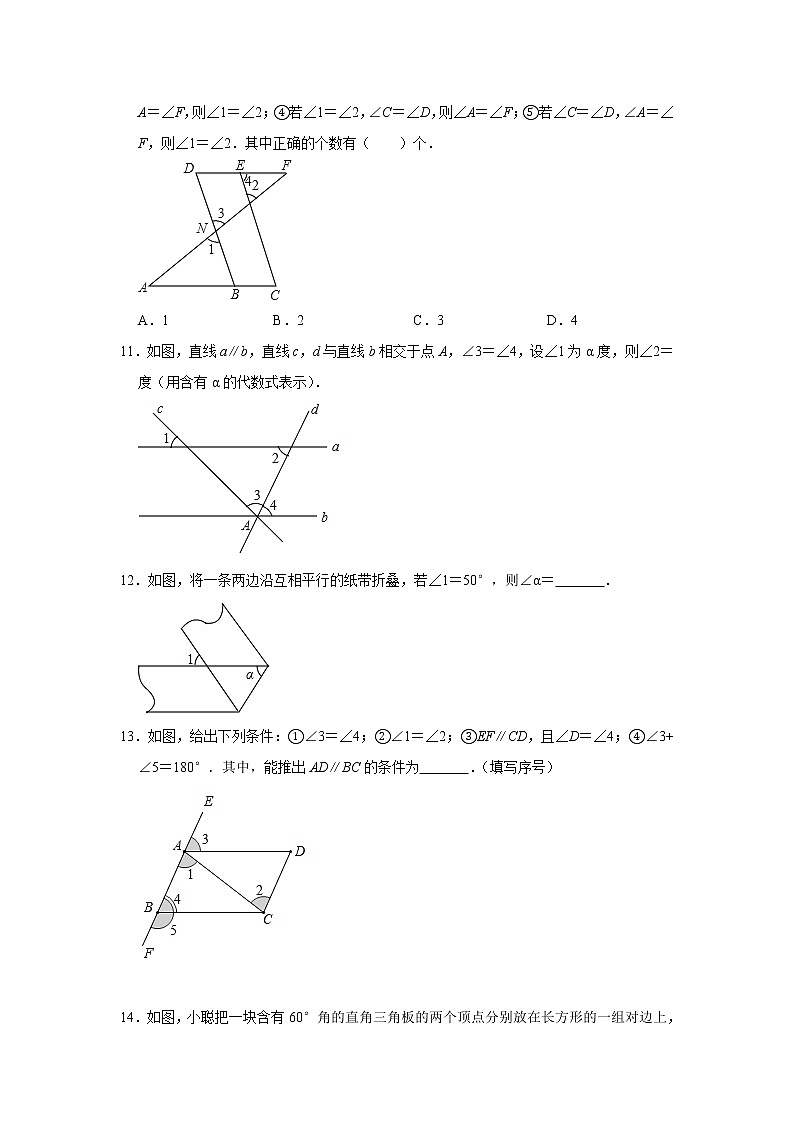
10.如图,下列命题:①若∠1=∠2,则∠D=∠4;②若∠C=∠D,则∠4=∠C;③若∠A=∠F,则∠1=∠2;④若∠1=∠2,∠C=∠D,则∠A=∠F;⑤若∠C=∠D,∠A=∠F,则∠1=∠2.其中正确的个数有( )个.
A.1 B.2 C.3 D.4
11.如图,直线a∥b,直线c,d与直线b相交于点A,∠3=∠4,设∠1为α度,则∠2= 度(用含有α的代数式表示).
12.如图,将一条两边沿互相平行的纸带折叠,若∠1=50°,则∠α= .
13.如图,给出下列条件:①∠3=∠4;②∠1=∠2;③EF∥CD,且∠D=∠4;④∠3+∠5=180°.其中,能推出AD∥BC的条件为 .(填写序号)
14.如图,小聪把一块含有60°角的直角三角板的两个顶点分别放在长方形的一组对边上,并测得∠1=26°,则∠2的度数是 .
15.若∠A与∠B的两边分别平行,且∠A比∠B的5倍少20°,则∠A的度数为 .
16.已知,如图,AB∥CD,∠ABE=40°,若CF平分∠ECD,且满足CF∥BE,则∠ECD的度数为 .
17.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠FEC=30°,∠ACF=20°,则∠DAC的度数为 °.
18.已知,如图,AB∥DC,AF平分∠BAE,DF平分∠CDE,且∠AFD比∠AED的2倍小10°,则∠AED的度数为 .
19.如图,将周长为6的△ABC沿BC方向平移1.5个单位得到△DEF,则四边形ABFD的周长为 .
20.如图,在△ABC中,∠BAC=35°,延长AB到点D,∠CBD=65°,过顶点A作AE∥BC,则∠CAE= °.
21.如图,已知BC∥DF,∠B=∠D,A、F、B三点共线,连接AC交DF于点E.
(1)求证:∠A=∠ACD.
(2)若FG∥AC,∠A+∠B=108°,求∠EFG的度数.
22.如图,已知∠1=∠BDE,∠2+∠FED=180°.
(1)证明:AD∥EF.
(2)若EF⊥BF于点F,且∠FED=140°.求∠BAC的度数.
23.如图,已知∠FED+∠BGF=180°,∠B=∠D.
(1)求证:AB∥DF;
(2)∠FED﹣∠AED=51°,∠FED﹣∠BEF=63°,求∠D.
24.已知点D在∠ABC内,E为射线BC上一点,连接DE,CD.
(1)如图1,点E在线段BC上,连接AE,∠AED=∠A+∠D.
①求证AB∥CD;
②过点A作AM∥ED交直线BC于点M,请猜想∠BAM与∠CDE的数量关系,并加以证明;
(2)如图2,点E在BC的延长线上,∠AED=∠A﹣∠D.若M平面内一动点,MA∥ED,请直接写出∠MAB与∠CDE的数量关系.
25.如图,AB∥CD,直线EF交直线AB、CD于点M、N,NP平分∠ENC交直线AB于点P,∠EMB=76°.
(1)求∠PNC的度数;
(2)若PQ将∠APN分成两部分,且∠APQ:∠QPN=1:3,求∠PQD的度数.
26.已知点F、G分别在直线AB、CD上,且知AB∥CD.
(1)如图1,请用等式表示∠GEF、∠BFE、∠CGE之间的数量关系并给出证明;
(2)如图2,∠BFE的平分线FQ所在的直线与∠CGE的平分线相交于点P,探究∠GPQ与∠GEF之间的数量关系,请直接写出你的结论: .
参考答案
1.解:∵BD∥CE,
∴∠BDC=∠1=76°,
∵∠BDC=∠2+∠A,
∴∠A=∠BDC﹣∠2=76°﹣28°=48°.
故选:C.
2.解:∵纸条的两边互相平行,
∴∠1=∠2,∠3=∠4,∠4+∠5=180°,故①,②,④正确;
∵三角板是直角三角板,
∴∠2+∠4=180°﹣90°=90°,
∵∠3=∠4,
∴∠2+∠3=90°,故③正确.
综上所述,正确的个数是4.
故选:D.
3.解:如图,∵∠D=90°,
∴∠DBC=90°﹣∠1=90°﹣82°=8°,
∴∠ABD=90°+8°=98°,
∵DG∥EF,
∴∠2=∠ABD=98°.
故选:B.
4.解:①若∠A+∠B=180°,则∠A,∠B互补,正确;
②若∠A+∠B=180°,则∠A,∠B是同旁内角,错误;
③若∠A,∠B互补,则∠A+∠B=180°,正确;
④若∠A,∠B是同旁内角,则∠A+∠B=180°,错误.
故选:B.
5.解:∵EG平分∠BEF,
∴∠GEB=∠BEF=34°,
∵∠1=∠BEF=68°,
∴CD∥AB,
∴∠EGF=∠GEB=34°,
故选:A.
6.解:∵∠1=58°,
∴∠EFD=∠1=58°.
∵AB∥CD,
∴∠EFD+∠BEF=180°,
∴∠BEF=180°﹣58°=122°.
∵EG⊥EF,
∴∠GEF=90°,
∴∠2=∠BEF﹣∠GEF
=122°﹣90°
=32°.
故选:B.
7.证明:∵AB∥CD,
∴∠EGF=∠DFG,
∵FG平分∠DEF,
∴∠EFG=∠DFG,
∴∠EFG=∠EGF,
∵∠BEF=70°,
∴∠AGF=∠EFG=(180°﹣70°)=55°,
故选:C.
8.解:∵a∥b,
∴∠4=∠5.
又∵∠2=∠4,
∴∠2=∠4.
故选:D.
9.解:过C作CM∥AB,
∵AB∥DE,
∴AB∥CM∥DE,
∴∠1+∠B=180°,∠2=∠D=35°,
∵∠B=130°,
∴∠1=50°,
∴∠BCD=∠1+∠2=85°,
故选:B.
10.解:①若∠1=∠2,可得∠3=∠2,可得DB∥EC,则∠D=∠4,正确;
②若∠C=∠D,得不出∠4=∠C,错误;
③若∠A=∠F,得不出∠1=∠2,错误;
④若∠1=∠2,∠C=∠D,则∠A=∠F,正确;
⑤若∠C=∠D,∠A=∠F,则∠1=∠2,正确.
故选:C.
11.解:∵直线a∥b,
∴∠5=∠1=α°,∠2=∠4,
∵∠3+∠4+∠5=180°,∠3=∠4,
∴∠3=∠4=(180°﹣α°)=90°﹣α°,
∴∠2=∠4=90°﹣α°;
故答案为:90﹣α.
12.解:如图所示:
∵纸片两边平行,
∴∠2=∠1=50°,
由折叠的性质得:2∠α+∠2=180°,
∴2∠α+50°=180°,
解得:∠α=65°.
故答案为:65°.
13.解:①∵∠3=∠4,∴AD∥BC;
②∵∠1=∠2,∴AB∥CD;
③∵EF∥CD,∴∠D=∠3,∵∠D=∠4,∴∠3=∠4,∴AD∥BC;
④∵∠3+∠5=180°,∠4+∠5=180°,∴∠3=∠4,∴AD∥BC,
故答案为:①③④
14.解:∵直尺的两边互相平行,∠1=26°,
∴∠3=∠1=26°,
∴∠2=60°﹣∠3=60°﹣26°=34°.
故答案为34°.
15.解:设∠B=x,则∠A=5x﹣20°,
由题意x=5x﹣20°,或x+5x﹣20°=180°,
解得x=5°或()°,
∴∠A=5°或()°
故答案为5°或()°.
16.解:如图,延长CE交AB于G,
∵AB∥CD,
∴∠AGE=∠ECD,∠BEG=∠FCE,
∵CF平分∠ECD,
∴可设∠DCF=∠GCF=α,
∴∠AGE=∠DCG=2α,∠BEG=∠FCG=α,
∵∠AGE是△BEG的外角,
∴∠AGE=∠BEG+∠B,
即2α=α+40°,
∴α=40°,
∴∠ECD=80°,
故答案为:80°.
17.解:∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠BCE=∠FEC=30°,
∵CE平分∠BCF,
∴∠BCF=2∠BCE=60°,
∴∠ACB=∠BCF+∠ACF=80°,
∵AD∥BC,
∴∠DAC+∠ACB=180°,
∴∠DAC=100°.
故答案为100.
18.解:如图所示,过F作FG∥AB,
∵AB∥DC,
∴AB∥GF∥CD,
∴∠1=∠DFG,∠2=∠AFG,
∴∠AFD=∠1+∠2,
∵AF平分∠BAE,DF平分∠CDE,
∴∠1=∠3,∠2=∠4,
设∠E=α,则∠AFD=2α﹣10°,
∴∠AFD=∠3+∠4=2α﹣10°,
∵四边形AEDF中,∠E+∠3+∠4+∠AFD=360°,
∴α+2(2α﹣10°)=360°,
解得α=76°,
故答案为:76°.
19.解:∵△ABC的周长为6,
∴AB+BC+AC=6,
∵△ABC沿BC方向平移1个单位得到△DEF,
∴AD=CF=1.5,AC=DF,
∴四边形ABFD的周长=AB+BC+CF+DF+AD=9,
故答案为:9.
20.解:∵AE∥BC,
∴∠CBD=∠EAB=65°,
∴∠CAE=∠EAB﹣∠BAC=65°﹣35°
=30°.
故答案为:30.
21.(1)证明:∵BC∥DF,
∴∠D+∠BCD=180°,
∵∠B=∠D,
∴∠B+∠BCD=180°,
∴AB∥CD,
∴∠A=∠ACD;
(2)解:∵∠A+∠B=108°,
∴∠ACB=72°,
∵FG∥AC,
∴∠BGF=72°,
∵BC∥DF,
∴∠EFG=72°.
22.解:(1)∵∠1=∠BDE,
∴AC∥DE,
∴∠2=∠ADE,
∵∠2+∠FED=180°,
∴∠ADE+∠DEF=180°,
∴AD∥EF;
(2)∵EF⊥BF,
∴∠F=90°,
∵AD∥EF,∠FED=140°,
∴∠FAD+∠F=180°,∠ADE+∠DEF=180°
∴∠DAF=90°,∠ADE=40°,
∴∠2=∠ADE=40°,
∴∠BAC=180°﹣∠2﹣∠DAF=50°.
23.解:(1)∵∠FED+∠BGF=180°,∠BGE+∠BGF=180°,
∴∠DEF=∠BGF,
∴AB∥DF;
(2)设∠FED=x,
∵∠FED﹣∠AED=51°,∠FED﹣∠BEF=63°,
∴∠AED=x﹣51°,∠BEF=x﹣63°,
∵∠AED+∠FED+∠BEF=180°,
∴x﹣51°+x+x﹣63°=180°,
∴x=98°,
∴∠AED=98°﹣51°=47°,
∵AB∥DF,
∴∠D=∠AED=47°.
24.解:(1)①如图1,过E作EF∥AB,则∠BAE=∠AEF,
∵∠AED=∠BAE+∠D,
∴∠D=∠AED﹣∠BAE,
又∵∠DEF=∠AED﹣∠AEF,
∴∠D=∠DEF,
∴EF∥CD,
∴AB∥CD;
②如图1,
∵AM∥DE,
∴∠MAE=∠AED,
∵∠AED=∠BAE+∠D,
∠MAE=∠BAE+∠BAM,
∴∠CDE=∠BAM;
(2)如图2,过E作EF∥AB,则∠BAE=∠AEF,
延长MA交BC于G,
∵∠AED=∠BAE﹣∠D,
∴∠D=∠BAE﹣∠AED,
又∵∠DEF=∠AEF﹣∠AED,
∴∠D=∠DEF,
∴CD∥EF,
∴AB∥CD,
∵MA∥ED,
∴∠DEC=∠MGB,
∵AB∥CD,
∴∠B=∠DCE,
∴∠D=∠BAG,
又∵∠BAG+∠MAB=180°,
∴∠CDE+∠MAB=180°,
当点M′在射线AG时,∠BAM′=∠CDE,
故MAB与∠CDE的数量关系是相等或互补.
25.解:(1)∵AB∥CD,
∴∠END=∠EMB=76°,
∴∠ENC=180°﹣∠END=104°,
∵NP平分∠ENC,
∴∠PNC=ENC=52°;
(2)∵∠APQ:∠QPN=1:3,
∴∠QPN=3∠APQ,
∵AB∥CD,
∴∠MPN=∠PNC=52°,
∴∠APN=180°﹣∠MPN=128°,
∴∠APQ+∠QPN=128°,
∴4∠APQ=128°,
∴∠APQ=32°,
∴∠PQD=∠APQ=32°.
则∠PQD的度数为32°.
26.解:(1)∠GEF=∠BFE+180°﹣∠CGE,证明如下:
如图1,过E作EH∥AB,
∵AB∥CD
∴AB∥CD∥EH,
∴∠HEF=∠BFE,∠HEG+∠CGE=180°,
∴∠HEF+∠HEG=∠BFE+180°﹣∠CGE,
∴∠GEF=∠BFE+180°﹣∠CGE;
(2)∠GPQ+∠GEF=90°,理由是:
∵FQ平分∠BFE,GP平分∠CGE,
∴∠BFQ=∠BFE,∠CGP=∠CGE,
△PMF中,∠GPQ=∠GMF﹣∠PFM=∠CGP﹣∠BFQ,
∴∠GPQ+∠GEF=∠CGE﹣∠BFE+∠GEF=×180°=90°.
故答案为:∠GPQ+∠GEF=90°
初中数学人教版七年级下册第五章 相交线与平行线综合与测试综合训练题: 这是一份初中数学人教版七年级下册第五章 相交线与平行线综合与测试综合训练题,共18页。试卷主要包含了如图,下列条件,如图所示,已知AB∥CD,则,将一张长方形纸片等内容,欢迎下载使用。
《第5章相交线与平行线》期末复习综合提升训练2(附答案)-2021-2022学年人教版七年级数学下册: 这是一份《第5章相交线与平行线》期末复习综合提升训练2(附答案)-2021-2022学年人教版七年级数学下册,共16页。
数学七年级下册第五章 相交线与平行线综合与测试课后复习题: 这是一份数学七年级下册第五章 相交线与平行线综合与测试课后复习题,共6页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。













