2020届四川省宜宾市第四中学校高三上学期期末考试数学（文）试题

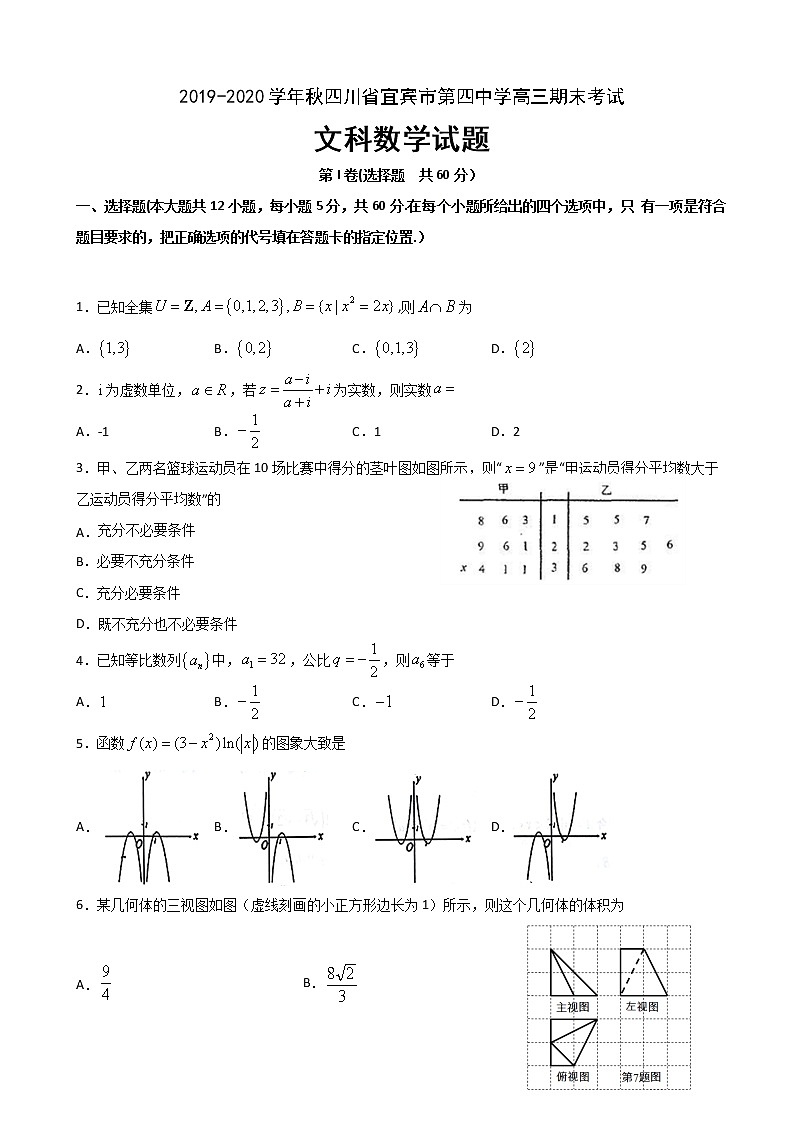
2019-2020学年秋四川省宜宾市第四中学高三期末考试

文科数学试题

第I卷(选择题  共60分）

一、选择题(本大题共12小题，每小题5分，共60分.在每个小题所给出的四个选项中，只 有一项是符合题目要求的，把正确选项的代号填在答题卡的指定位置.）

1．已知全集,则为

A． B． C． D．

2．为虚数单位，，若为实数，则实数[来源:Zxxk.Com]

A．-1 B． C．1 D．2

3．甲、乙两名篮球运动员在10场比赛中得分的茎叶图如图所示，则“”是“甲运动员得分平均数大于乙运动员得分平均数”的

A．充分不必要条件 

B．必要不充分条件

C．充分必要条件 

D．既不充分也不必要条件

4．已知等比数列中，，公比，则等于

A． B． C． D．

5．函数的图象大致是

A． B． C． D．

6．某几何体的三视图如图（虚线刻画的小正方形边长为1）所示，则这个几何体的体积为

A．               B． 

C．                D．

7．在边长为的正方形中，为的中点，点在线段

上运动，则的取值范围是

A． B． C． D．

8．设g(x)的图象是由函数f(x)＝cos2x的图象向左平移个单位得到的，则g()等于

A．1 B． C．0 D．－1

9．在普通高中新课程改革中，某地实施“3+1+2”选课方案．该方案中“2”指的是从政治、地理、化学、生物4门学科中任选2门，假设每门学科被选中的可能性相等，那么政治和地里至少有一门被选中的概率是

A． B． C． D．

10．在中，，，，则在方向上的投影是

A．4 B．3 C．-4 D．-3

11．已知a＞0，x，y满足约束条件,若z=2x+y的最小值为1，则

A．    B．    C．1    D．2

12．若曲线在点处的切线方程为，且点在直线（其中，）上，则的最小值为

A． B． C． D．

第Ⅱ卷（非选择题共90分）

二、填空题(本大题共4小题，每小题5分，满分20分）

13．已知向量，，若，则__________．

14．已知函数，则的值域为______.

15．已知是定义在上的奇函数，对于任意且，都有成立，且，则不等式的解集为_____[来源:学+科+网]

16．在三棱锥中，平面平面，是边长为的等边三角形，其中，则该三棱锥外接球的表面积为_____．

三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤，第17 ~ 21题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答.）[来源:Zxxk.Com]

17.（12分）某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在内，发布成绩使用等级制.各等级划分标准见下表.

规定：三级为合格等级，D为不合格等级.为了解该校高一年级学生身体素质情况，从中抽取了名学生的原始成绩作为样本进行统计.按照的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示.

（I）求和频率分布直方图中的的值，并估计该校高一年级学生成绩是合格等级的概率；

（II）在选取的样本中，从两个等级的学生中随机抽取2名学生进行调研，求至少有一名学生是等级的概率．

18．（12分）在锐角中，角的对边分别为，.

（I）求角的大小；

（II）若，求的取值范围.

19．（12分）如图，在三棱锥中，是等边三角形，，点P是AC的中点，连接BP，DP

（I）证明：平面平面BDP；

（II）若，，求三棱锥的体积．

20．（12分）已知椭圆的两个焦点分别为，长轴长为．

（Ⅰ）求椭圆的标准方程及离心率；

（Ⅱ）过点的直线与椭圆交于，两点，若点满足，求证：由点 构成的曲线关于直线对称．

21．（12分）已知函数．[来源:学科网ZXXK]

（Ⅰ）当时，求函数的极值；

（Ⅱ）若函数有两个零点，求的取值范围，并证明．

（二）选考题：共10分，请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.

22. （10分） [选修4-4：坐标系与参数方程]

在直角坐标系中，圆C的参数方程为，其中为参数，以坐标原点为极点，轴正半轴为极轴建立极坐标系．

（Ⅰ）求圆的极坐标方程；

（Ⅱ）为圆上一点，且点的极坐标为，射线绕点逆时针旋转，得射线，其中也在圆上，求的最大值．

23．（10分）已知函数，

（Ⅰ）当时，解不等式；

（Ⅱ）若存在满足，求实数的取值范围．

2019-2020学年秋四川省宜宾市第四中学高三期末考试

文科数学试题参考答案

1．B 2．C 3．A 4．C 5．A 6．D 7．C 8．D 9．D 10．D 11．B 12．C

13．  14．.  15．  16．

17．（I）由题意可知，样本容量

因为成绩是合格等级人数为：人，抽取的50人中成绩是合格等级的频率为，依据样本估计总体的思想，所以，该校高一年级学生成绩是合格等级的概率为

（II）由茎叶图知，等级的学生共有3人，等级学生共有人，记等级的学生为，

等级学生为，则从8名学生中随机抽取2名学生的所有情况为：

共28个基本事件[来源:学科网]

记“至少有一名学生是等级”事件为，则事件的可能结果为

共10种

因此

18．（1）由=

得sinAcosB+sinAcosC=cosAsinB+cosAsinC，

即sin（A﹣B）=sin（C﹣A），

则A﹣B = C﹣A，即2A=C+B，

即A=．.

（2）当a=时，∵B+C=，∴C=﹣B．由题意得 ，

∴＜B＜．由 =2，得 b=2sinB，c=2sinC，

∴b2+c2=4 （sin2B+sin2C）=4+2sin（2B﹣）．

∵＜B＜，∴＜sin（2B﹣）≤1，∴1≤2sin（2B﹣）≤2．

∴5＜b2+c2≤6．

故的取值范围是.

19．证明：如图所示，

因为是等边三角形，，

所以≌，可得，

又因为点P是AC的中点，则，，

又，平面PBD，平面PBD，

所以平面平面BDP；

设，在中，，则；

在等边中，，

在等腰中，；

在中，由，得；

由余弦定理得，

即，解得；

所以的面积为，

所以三棱锥的体积为．

20．（Ⅰ）由已知，得，所以，

又，所以

所以椭圆的标准方程为，离心率.

（Ⅱ）设，，  ，

①直线 与轴垂直时，点的坐标分别为，．

因为，，，

所以．

所以，即点与原点重合;

②当直线与轴不垂直时，设直线的方程为，

由 得，．

所以.

则，

因为，，，

所以．

所以，．，，

消去得．

综上，点构成的曲线的方程为

对于曲线的任意一点，它关于直线的对称点为．

把的坐标代入曲线的方程的左端：．

所以点也在曲线上．所以由点构成的曲线关于直线对称.

21：（1）由得，

当时，，若；若 ，

故当时，在处取得的极大值；函数无极小值.

（2）当时，由（1）知在处取得极大值，且当趋向于时，趋向于负无穷大，又有两个零点，则，解得.

当时，若；若；若，则在处取得极大值，在处取得极小值，由于，则仅有一个零点.

当时，，则仅有一个零点.

当时，若；若；若，则在处取得极小值，在处取得极大值，由于，则仅有一个零点.

综上，有两个零点时，的取值范围是.

两零点分别在区间和内，不妨设.

欲证，需证明，

又由（1）知在单调递减，故只需证明即可.

，

又，

所以，

令，则，

则在上单调递减，所以，即，

所以.

22．解：（1），

由可得圆的极坐标方程．

（2）由题意可知：,所以

，所以，

从而最大值为．

23．（1）当时，

当时，，解得：；

当时，，解得：；

当时，，解得：的解集为：

（2）若存在满足等价于有解

    ，解得：

实数的取值范围为：