初中数学人教版八年级下册19.1.1 变量与函数教课内容ppt课件

这是一份初中数学人教版八年级下册19.1.1 变量与函数教课内容ppt课件，共19页。PPT课件主要包含了和－2，和－8，和－18，和－32，顺序不要反，，确定自变量的取值范围，例3已知函数，函数的发展史等内容，欢迎下载使用。

如图,水滴激起的波纹可以看成是一个不断向外扩展的圆,它的面积随着半径的变化而变化 ,随着半径的确定而确定.这就是我们要研究的和此有关的问题——函数.
想一想：如果你坐在摩天轮上，随着时间的变化，你离开地面的高度是如何变化的？
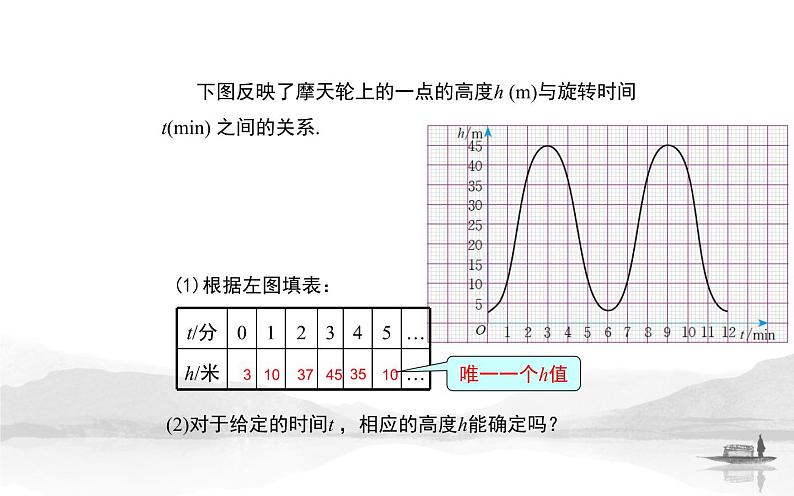
下图反映了摩天轮上的一点的高度h (m)与旋转时间t(min) 之间的关系.
(2)对于给定的时间t ，相应的高度h能确定吗？
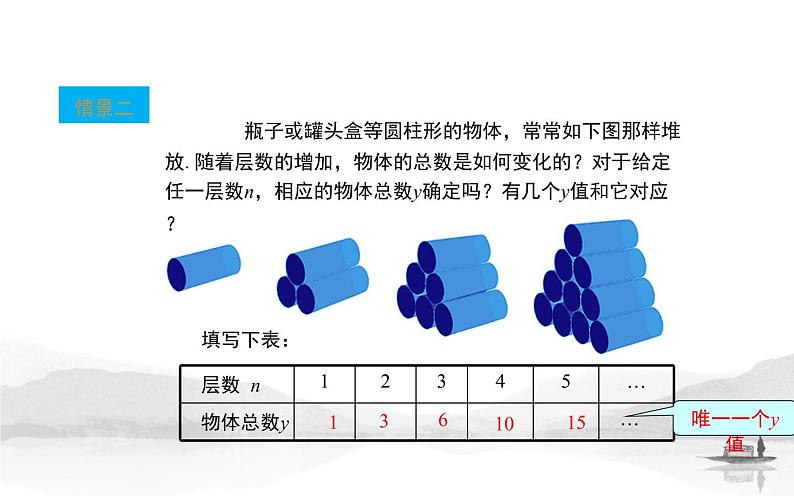
瓶子或罐头盒等圆柱形的物体，常常如下图那样堆放.随着层数的增加，物体的总数是如何变化的？对于给定任一层数n，相应的物体总数y确定吗？有几个y值和它对应？
一定质量的气体在体积不变时，假若温度降低到 -273℃，则气体的压强为零.因此，物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系：T=t+273，T≥0.
(1)当t分别等于-43，-27，0，18时，相应的热力学温度T是多少？
(2)给定任一个大于-273 ℃的摄氏温度t值，相应的热力学温度T确定吗？有几个T值和它对应？
230K、246K 、273K、291K
思考：上面的三个问题中，各变量之间有什么共同特点？
共同特点：都有两个变量，给定其中某一个变量的值，相应地就确定了另一个变量的值.
一般地，在某个变化过程中，如果有两个变量x与y，并且对于x的每一个确定的值，y都有唯一确定的值与它对应，那么我们就说x是自变量，y是x的函数. 如果当x=a时y=b，那么b叫做当自变量的值为a时的函数值.
例1：填表并回答问题：（1）对于x的每一个值，y都有唯一的值与之对应吗？答： . （2）y是x的函数吗？为什么？
答：不是，因为y的值不是唯一的.
关键词：两个变量，给一个x，得一个y.易错点：
1:下列关于变量x ，y 的关系式：y =2x+3；y =x2+3；y =2|x|；④ ；⑤y2-3x=10，其中表示y 是x 的函数关系的是 ．
2.下列各表达式不是表示y是x的函数的是( )
A. B. C D.
　　问题：请用含自变量的式子表示下列问题中的函数关系：　 （1）汽车以60 km/h 的速度匀速行驶，行驶的时间为 t（单位：h），行驶的路程为 s（单位：km）；　 （2）多边形的边数为 n，内角和的度数为 y．
t 取-2 有实际意义吗？
思考：你认为函数的自变量可以取任意值吗？
归纳总结：在实际问题中，函数的自变量取值范围往往是有限制的，在限制的范围内，函数才有实际意义；超出这个范围，函数没有实际意义，我们把这种自变量可以取的数值范围叫函数的自变量取值范围．
例2: 汽车的油箱中有汽油50L，如果不再加油，那么油箱中的油量y（单位：L）随行驶里程x（单位：km）的增加而减少，平均耗油量为0.1L/km.
（1）写出表示y与x的函数关系的式子.
解:(1) 函数关系式为: y = 50－0.1x
（2）指出自变量x的取值范围；
由x≥0及50－0.1x ≥0得0 ≤ x ≤ 500 ∴自变量的取值范围是 0 ≤ x ≤ 500
（3）汽车行驶200 km时，油箱中还有多少油？
当 x = 200时,函数 y 的值为y=50－0.1×200=30.
因此,当汽车行驶200 km时,油箱中还有油30L
汽车行驶里程，油箱中的油量均不能为负数！
(1)求当x=2，3，-3时，函数的值；(2)求当x取什么值时，函数的值为0.
解：（1）当x=2时，y= ; 当x=3时，y= ; 当x=-3时，y=7 ;
（2）令 解得x= 即当x= 时，y=0.
把自变量x的值带入关系式中，即可求出函数的值.
1：下列函数中自变量x的取值范围是什么？
2.油箱中有油30kg,油从管道中匀速流出，1h流完，则油箱中剩余油量Q（kg）与流出时间t（min）之间的函数关系式是 ，自变量t的取值范围是 .
最早提出函数概念的，是１７世纪德国数学家莱布尼茨。
有一个大胆的人定义了函数
1718年约翰·伯努利对函数概念进行了定义，并强调函数要用公式来表示。
1755年欧拉给出了函数定义。