试卷 专题12《旋转》

专题12《旋转》

破解策略

经过旋转，对应线段相等，对应角相等；任意两条对应线段所在直线的夹角都等于旋转角；旋转前后的图形全等．

l．旋转的基本图形有：

（1）如图，将∠AOB旋转至∠A 'OB '，则∠AOA'＝∠BOB'．

（2）如图，将△AOB旋转至△ A'OB '，连结AA'， BB'，则△AOA ' ∽△BOB'

2．利用旋转性质解题的步骤为：

（1）找旋转点，得等边、等角；

（2）证全等或相似；

（3）利用全等或者相似得到边、角关系．

例题讲解
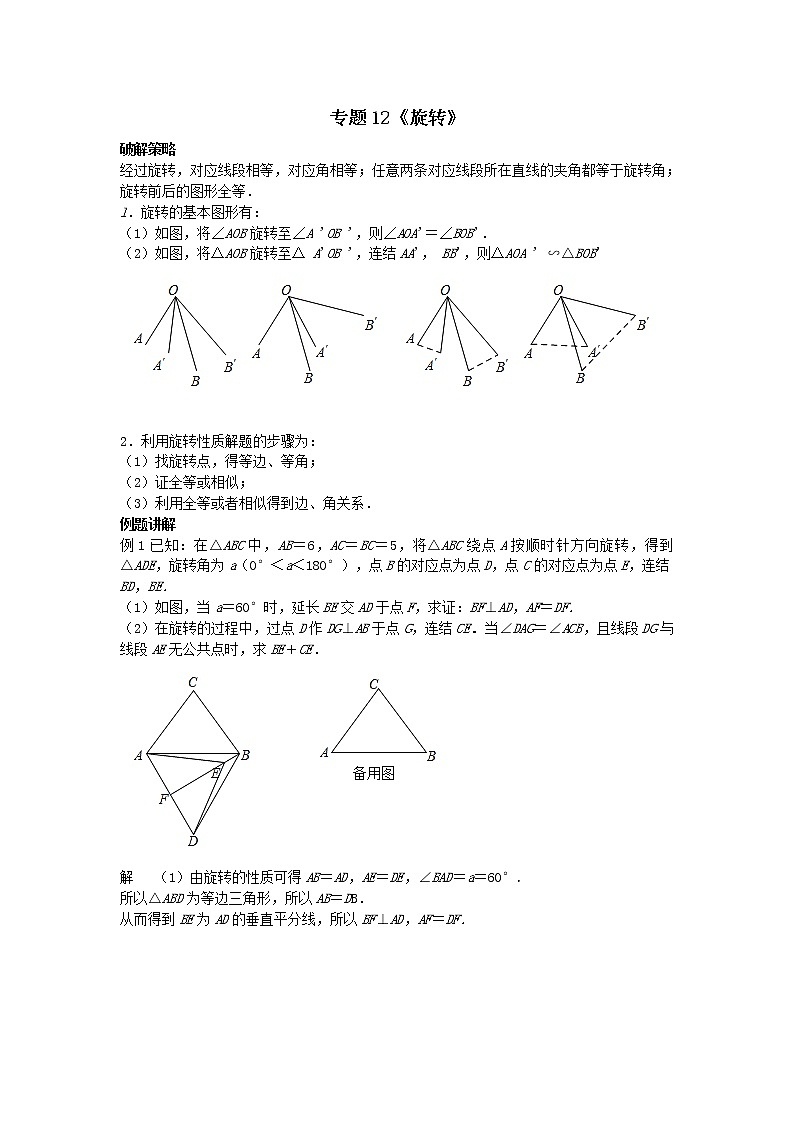
例1已知：在△ABC中，AB＝6，AC＝BC＝5，将△ABC绕点A按顺时针方向旋转，得到△ADE，旋转角为a（0°＜a＜180°），点B的对应点为点D，点C的对应点为点E，连结BD，BE．
（1）如图，当a＝60°时，延长BE交AD于点F，求证：BF⊥AD，AF＝DF．
（2）在旋转的过程中，过点D作DG⊥AB于点G，连结CE．当∠DAG＝∠ACB，且线段DG与线段AE无公共点时，求BE＋CE．

解   （1）由旋转的性质可得AB＝AD，AE＝DE，∠BAD＝a＝60°．
所以△ABD为等边三角形，所以AB＝DB．
从而得到BE为AD的垂直平分线，所以BF⊥AD，AF＝DF．

（2）如图，按照题意画出图形，令CE与AB的交点为H．
由旋转的性质可得CA＝CB＝EA＝ED，∠CAB＝∠CBA
＝∠EAD＝∠EDA．
因为∠DAG＋∠DAE＋∠EAB＝∠ACB＋∠CAB＋∠CBA＝180°，且已知∠DAG＝∠ACB，
所以∠CAB＝∠EAB．
所以AB，CE互相垂直平分，则AC＝CB＝BE＝EA．

所以BE＋CE＝5＋．

例2已知：如图，△ABC是等边三角形，点E在线段AB上，点D在直线BC上，且ED＝EC，将△BCE绕点C顺时针旋转60°至△ACF，连结EF．
（1）求证：AB＝DB＋AF；
（2）若点E在线段AB的延长线上，其他条件不变，线段AB，DB，AF之间有怎样的数量关系?请说三明理由；
（3）若点E在线段BA的延长线上，其他条件不变，线段AB，DB，AF之间有怎样的数量关系？请说明理由．

证明  （1）如图1，过点E作EG∥AC交BC干表G，则△EBG为等边三角形．
易证△EBD≌△EGC，所以DB＝CG＝AE．由旋转的性质可得AF＝BE，所以AB＝BE＋AE＝AF＋DB．

（2）AB＝DB－AF．理由如下：

如图2，过点E作EG∥AC，交CD于点G，则△EBG为等边三角形．

易证△EGD≌△EBC，所以DG＝BC＝AB．

由旋转的性质可得AF＝BE＝BG．

所以AB＝DG＝DB－AF．

（3）AB＝AF－DB．理由如下：

如图3，过点E作EG∥AC，交BC的延长线于点G，则△EBG为等边三角形．

易证△EBD≌△EGC，

所以DB＝CG＝AE．

由旋转的性质可得AF＝BE，

所以AB＝BE－AE＝AF－DB．

进阶训练

1．如图，将正五边形ABCDE绕点A顺时针旋转60°后，旋转前后两图形有另一交点O，连结AO；再将AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连结PO，判断△AOP的形状，并说明理由．

1．△AOP为等边三角形．

【提示】由旋转的性质得∠EAE'＝∠PAO＝60°，从而∠EAP＝∠E'AB，又∠E＝∠E'，AE＝AE'，从而△PEA≌△OE'A，则AP＝AO，即得证．

2．如图，在菱形ABCD中，AC＝2，BD＝，AC，BD相交于点O，将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F，连结EF，与AC相交于点G．

（1）判断△AEF是哪一种特殊三角形，并说明理由；

（2）旋转过程中，当点E为边BC的四等分点时（BC＞CE），求CG的长．

2．（1）△AEF是等边三角形；（2）CG＝．

【提示】（1）证△ABE≌△ACF（ASA）即可；

（2）易证△CAE∽△CFG，从而，即可求得CG的长．