- 试卷 专题3《函数图象的公共点》 试卷 5 次下载
- 试卷 专题4《图形的分割与拼接》 试卷 5 次下载
- 试卷 专题6《轴对称之最短路径》 试卷 7 次下载
- 试卷 专题7《旋转之求线段最值》 试卷 6 次下载
- 试卷 专题8《“PA+k•PB”型的最值问题》 试卷 7 次下载
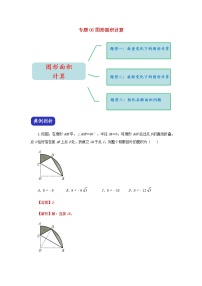
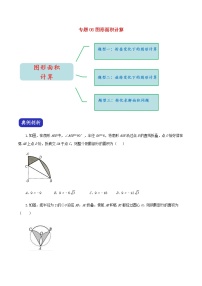
试卷 专题5《等分图形面积》
展开专题5《等分图形面积》
破解策略
等分图形面积的过程中,常用等积变换法,等积变换的基本图形为:
如图,,点在上,点B,C在上,则.
图形等分面积的常见类型有:
(1)已知:△ABC.
作法:作中线AD.
结论:直线AD平分△ABC的面积.
(2)已知:平行四边形ABCD.
作法:过对角线交点O作直线.
结论:过点O的直线平分平行四边形ABCD的面积.
(3)已知:梯形ABCD,AD∥BC.
作法:过中位线EF中点O(或上、下底边中点连线HG的中点O)作直线,且与上、下底均相交.
结论:过点O且与上、下底均相交的直线平分梯形ABCD的面积.
(4)已知:△ABC,P为AC边上的定点.
作法:作△ABC的中线AD,连结PD,过点A作AE∥PD,交BC于点E.
结论:直线PE平分△ABC面积.
(5)已知:四边形ABCD.
作法:连结AC,过点D作DE∥AC,交BC的延长线于点E,连结AE,作△ABE的中线AF.
结论:直线AF平分平行四边形ABCD的面积.
(6)已知:四边形ABCD,点P为AD上的定点.
作法:连结PB,PC.作AE∥PB,DF∥PC,分别交直线BC于点E,F,连结PE,PF,作△PEF的中线PG.
结论:直线PG平分四边形ABCD的面积.
(7)已知:五边形ABCDE.
作法:连结AC,AD,作BF∥AC,EG∥AD,分别交直线CD于点F,G,连结AF,AG,作△AFG的中线AH.
结论:直线AH平分五边形ABCDE的面积.
进阶训练
1.如图,已知五边形ABOCD各定点坐标为A(3,4),B(0,2),O(0,0),C(4,0),D(4,2),请你构造一条经过顶点A的直线,将五边形ABOCD平分为面积相等的两部分,并求出该直线的表达式.
答:如图:
直线的表达式为.
【提示】 连结AO,作BM∥AO交x轴于点M,连结AC,作DN∥AC交x轴于点N,取MN中点F,则直线AF将五边形ABOCD分为面积相等的两部分.作AH⊥x轴于点H,则△BMO∽△AOH,可得点M的坐标.同理可得点N的坐标.从而求得点F的坐标.确定直线AF的表达式.
2.过四边形ABCD的一个顶点画一条直线,把四边形ABCD的面积分成1:2的两部分.
答:如图:
【提示】 连结AC,过点D作DE∥AC交BC的延长线于点E,取BE的一个三等分点F或G,则直线AF或AG即为所求.
3.设w是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与w的面积相等(简称等积),那么这样的等积转化称为w的“化方”.
(1)阅读填空
如图1,已知矩形ABCD,延长AD到点E,使DE=DC,以AE为直径作半圆,延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.
理由:连结AH,EH.
因为AE为直径,所以∠AHE=90°,
所以∠HAE+∠HEA=90°.
因为DH⊥AE,所以∠ADH=∠EDH=90°.
所以∠AHD=∠HED,所以△ADH∽ .
所以,即
因为DE=DC,
所以= ,即正方形DFGH与矩形ABCD等积
(2)操作实践
平行四边形的“化方”思路是:先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.
如图2,请作出与平行四边形ABCD等积的正方形(不要求写出具体作法,保留作图痕迹).
(3)解决问题
三角形的“化方”思路是:先把三角形转化为等积的 (填写图形名称),再转化为等积的正方形.
如图3,△ABC的顶点再正方形网格的格点上,请作出与△ABC等积的正方形(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).
3.(1)△HDE;AD·DC;
(2)作图如下:
(3)矩形;作图如下:
(4)作图如下:
【提示】(2)作法:①分别过点A,D作直线BC的垂线,垂足分别为;
②延长AD至点E,使得;
③以AE为直径作半圆;
④延长交半圆于点H;
⑤以DH为边向右作正方形DFGH.
则正方形DFGH与平行四边形ABCD等积.
(3)作法:
①作△ABC的中位线MN;
②分别过点B,C作MN的垂线,垂足分别为E,D;
③延长BC至点F,使得CF=CD;
④以BF为直径作半圆;
⑤延长DC交半圆于点G;
⑥以CG为边向右作正方形CGHI.
则正方形CGHI与△ABC等积.
(4)作法:
①连结BD,过点A作AE∥BD交CD的延长线于点E;
②作△EBC的中位线MN;
③分别过点B,C作MN的垂线,垂足分别为F,G;
④延长BC至点H使得CH=CG;
⑤以BH为直径作半圆;
⑥延长GC交半圆于点I;
⑦以CI为边向右作正方形CIJK.
则正方形CIJK与四边形ABCD等积.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4)拓展探究
n边形(n>3)的“化方”思路之一是:把村边形转化,为等积的”1边形.…一直至转化为等积的三角形,从而实现化方.
如图4,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形 ABCD等积的正方形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作圈)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
专题25 图形面积的计算_答案: 这是一份专题25 图形面积的计算_答案,共5页。试卷主要包含了625, , 18, 8, B 提示, B等内容,欢迎下载使用。
专题25 图形面积的计算: 这是一份专题25 图形面积的计算,共9页。试卷主要包含了常见图形面积的计算,非常规图形面积的计算等内容,欢迎下载使用。
中考几何模型压轴题 专题5《等分图形面积》: 这是一份中考几何模型压轴题 专题5《等分图形面积》,共9页。