






数学选修4-1二 平行线分线段成比例定理示范课课件ppt
展开1.掌握平行线分线段成比例定理及其推论.2.能利用平行线分线段成比例定理及推论解决有关问题.
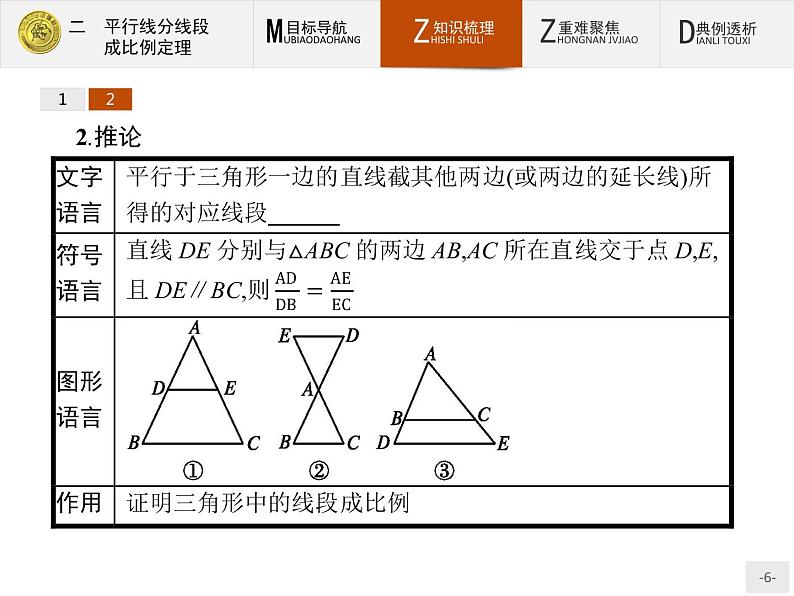
1.平行线分线段成比例定理
名师点拨1.定理的条件与平行线等分线段定理的条件相同,它需要a,b,c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a,b,c相交,即被平行线a,b,c所截.平行线的条数还可以更多.3.当截得的对应线段成比例,且比值为1时,则截得的线段相等,因此平行线分线段成比例定理是平行线等分线段定理的扩充,而平行线等分线段定理是平行线分线段成比例定理的特例;平行线等分线段定理是证明线段相等的依据,而平行线分线段成比例定理是证明线段成比例的依据.
【做一做2-2】 如图,AB∥CD,AC,BD相交于O点,若BO=7,DO=3,AC=25,则AO的长为( )A.10D.17.5
比例的有关概念及性质剖析:(1)线段的比:用同一个长度单位去量两条线段,所得的长度比叫做这两条线段的比.(2)比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.
(5)线段的比与比例线段是既有区别又有联系的两个概念.线段的比是对两条线段而言的,而比例线段是对四条线段而言的.线段的比有顺序性,a∶b与b∶a通常是不相等的;比例线段也有顺序性,如线段a,b,c,d成比例与线段a,c,b,d成比例不同.
【例1】 如图,AD为△ABC的中线,在AB上取点E,AC上取点F,使AE=AF.分析:这道题目要证的比例中的线段都没有直接的联系,可以考虑把比例转移,过点C作CM∥EF,交AB于点M,交AD于点N,且BC的中点为D,可以考虑补出一个平行四边形来证明.
证明:如图,过点C作CM∥EF,交AB于点M,交AD于点N.∵AE=AF,∴AM=AC.∵AD为△ABC的中线,∴BD=CD.延长AD到点G,使得DG=AD,连接BG,CG,则四边形ABGC为平行四边形.∴AB=GC.又∵AB∥GC,AM=AC,GC=AB,
反思1.比例线段常由平行线产生,因而研究比例线段问题应注意平行线的应用,在没有平行线时,可以添加平行线来促成比例线段的产生.2.利用平行线产生比例或转移比例是常用的证题技巧,当题中没有平行线而有必要转移比例时,也常添加辅助平行线,从而达到转移比例的目的.
【变式训练1】 如图,在△ABC(AB>AC)的边AB上取一点D,在边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.求证:BP∶CP=BD∶CE.
反思在利用平行线证明或计算时,常常根据已知条件将复杂的图形进行分解,从中找出基本图形,“借图解题”.
【变式训练2】 如图,在梯形ABCD中,AD∥BC,F为对角线AC上一点,FE∥BC交AB于点E,DF的延长线交BC于点H,DE的延长线交CB的延长线于点G.求证:BC=GH.
反思证明有关线段倒数和的等式时,常用的方法是首先将其变形为线段比的和为定值的形式,然后化归为同一直线上的线段比.
【变式训练3】 如图,在梯形ABCD中,AD∥BC,EF经过梯形对角线的交点O,且EF∥AD.(1)求证:OE=OF;
【例4】 如图,M是▱ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F,交CB的延长线于点N,若AE=2,AD=6.求AF∶AC的值.分析:AD∥BC,AM=MB⇒AE=BN⇒AF∶AC的值
反思运用平行线分线段成比例定理及推论来计算比值,应分清相关三角形中的平行线段及所截的边,并注意在求解过程中运用比例的等比性质、合比性质等.
高中数学人教版新课标A选修4-1二 平行线分线段成比例定理背景图ppt课件: 这是一份高中数学人教版新课标A选修4-1二 平行线分线段成比例定理背景图ppt课件,共8页。
2020-2021学年二 平行线分线段成比例定理习题ppt课件: 这是一份2020-2021学年二 平行线分线段成比例定理习题ppt课件,共3页。
高中数学人教版新课标A选修4-1第一讲 相似三角形的判定及有关性质二 平行线分线段成比例定理教课内容ppt课件: 这是一份高中数学人教版新课标A选修4-1第一讲 相似三角形的判定及有关性质二 平行线分线段成比例定理教课内容ppt课件,共8页。PPT课件主要包含了课前热身,课上练习,知识1,知识2,总结推论,课前热身单击,想一想,课上练习填空等内容,欢迎下载使用。













