高中数学人教版新课标A选修2-12.3双曲线多媒体教学ppt课件

这是一份高中数学人教版新课标A选修2-12.3双曲线多媒体教学ppt课件，共20页。PPT课件主要包含了对称性，渐近线，离心率，提升总结，弦长公式，变式练习等内容，欢迎下载使用。

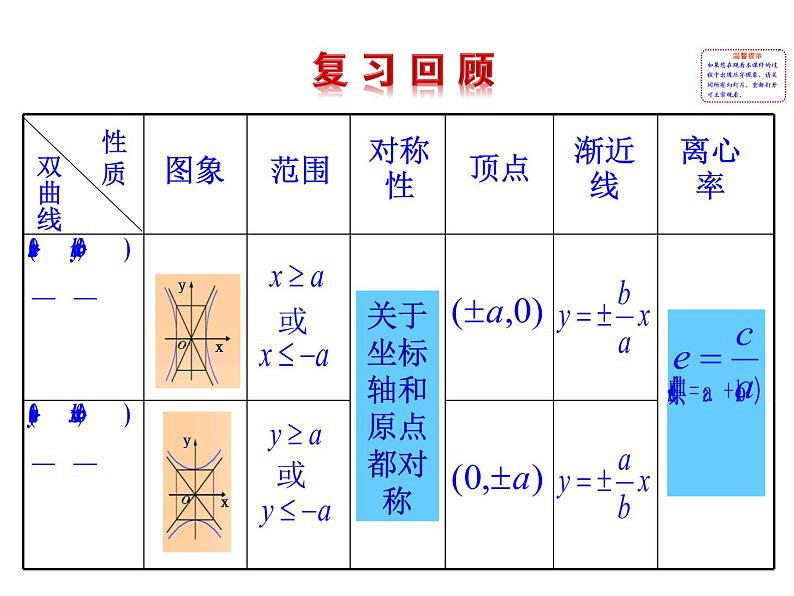
关于坐标轴和原点都对称
顶点
1.了解双曲线的几何性质，并会应用于实际问 题之中.（重点）2.会利用双曲线的定义、标准方程、几何性质 及图形四者之间的内在联系，分析和解决实 际问题.（重点、难点）
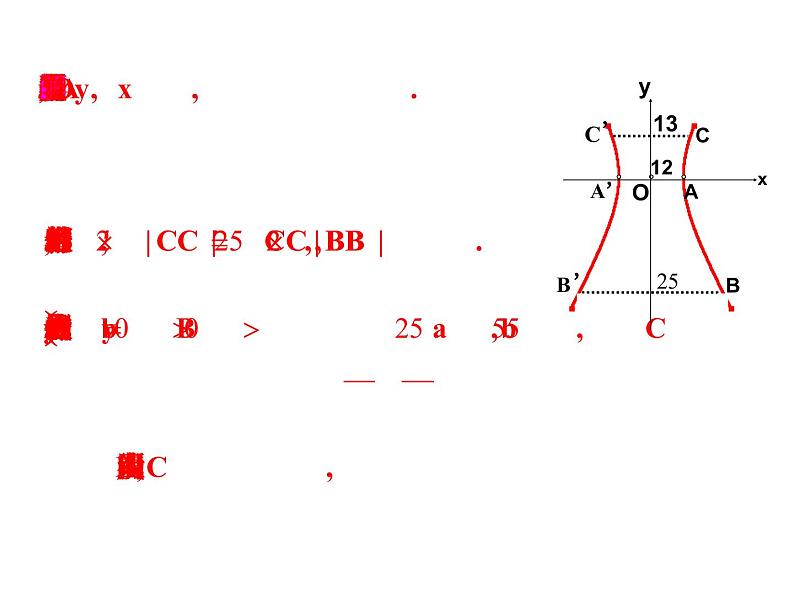
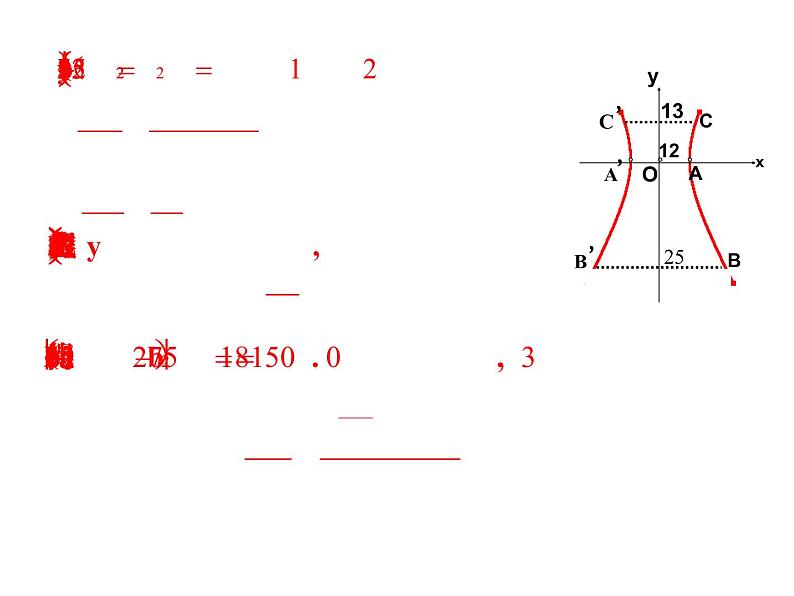
探究点1 由双曲线的性质求双曲线方程
已知双曲线的几何性质，求其标准方程的方法步骤：(1)确定焦点所在的位置，以确定双曲线方程的形式；(2)确立关于a,b,c的方程(组)，求出参数a,b,c；(3)写出标准方程．
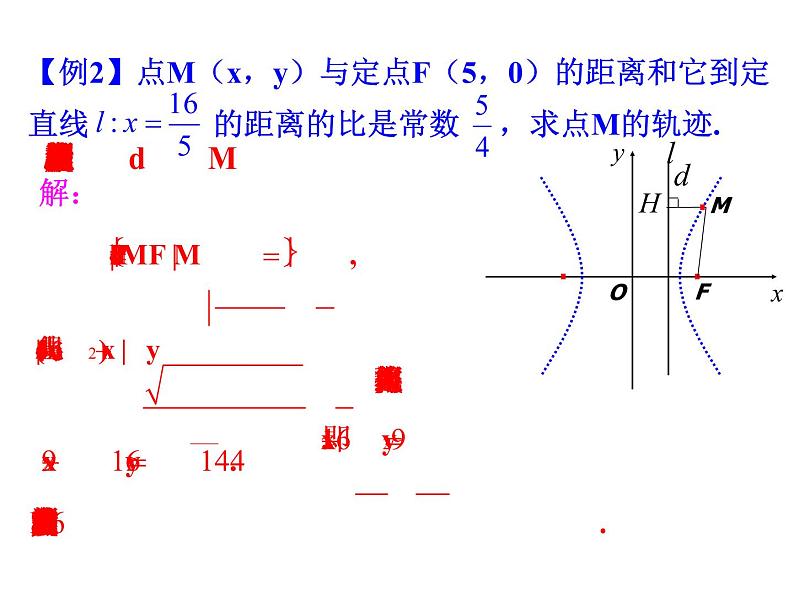
【例2】点M（x，y）与定点F（5，0）的距离和它到定直线 的距离的比是常数 ，求点M的轨迹.
双曲线中应注意的几个问题：(1)双曲线是两支曲线，而椭圆是一条封闭的曲线；(2)双曲线的两条渐近线是区别于其他圆锥曲线所特有的；(3)双曲线只有两个顶点，离心率e>1；(5)注意双曲线中a，b，c，e的等量关系与椭圆中a，b，c，e的不同．
种类: 相离; 相切; 相交(一个交点, 两个交点)
探究点2 直线与双曲线的位置关系
1.位置关系：相交、相切、相离2.判别方法(代数法) 联立直线与双曲线的方程， 消元得到一元二次方程（当二次项系数不为0时） (1)△>0直线与双曲线相交有两个公共点； (2)△=0 直线与双曲线相切有且只有一个 公共点； (3)△<0 直线与双曲线相离无公共点．
直线与双曲线的位置关系：
解：由双曲线的方程得，两焦点分别为F1(-3,0),F2(3,0).
因为直线AB的倾斜角是30°，且直线经过右焦点F2，所以，直线AB的方程为
这里我们也可以利用弦长公式求解.
算一算，看结果一样吗？
解析：因为F1的坐标是(-3,0),所以
2．过双曲线的一个焦点F2作垂直于实轴的弦PQ，点F1是另一个焦点，若∠PF1Q＝90°，则双曲线的离心率等于________．
4．求一条渐近线方程是3x＋4y＝0，一个焦点是(4,0)的双曲线标准方程． 解析：因为双曲线的一条渐近线方程为3x＋4y＝0，
1.双曲线的简单几何性质，利用性质求方程，解决与性质相关的综合性问题；2.掌握直线与双曲线的位置关系及弦长公式.