初中数学沪教版 (五四制)八年级下册20.2 一次函数的图像优秀同步测试题

这是一份初中数学沪教版 (五四制)八年级下册20.2 一次函数的图像优秀同步测试题，共13页。试卷主要包含了已知一次函数，若一次函数等内容，欢迎下载使用。


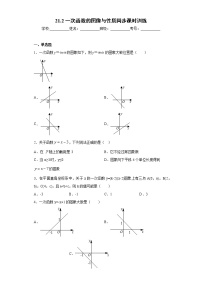
1．如图，直线与双曲线在第一象限内的交点R，与轴、轴的交点分别为P、Q．过R作RM⊥轴，M为垂足，若△OPQ≌△MPR，则的值是（ ）
A．1B．2C．D．
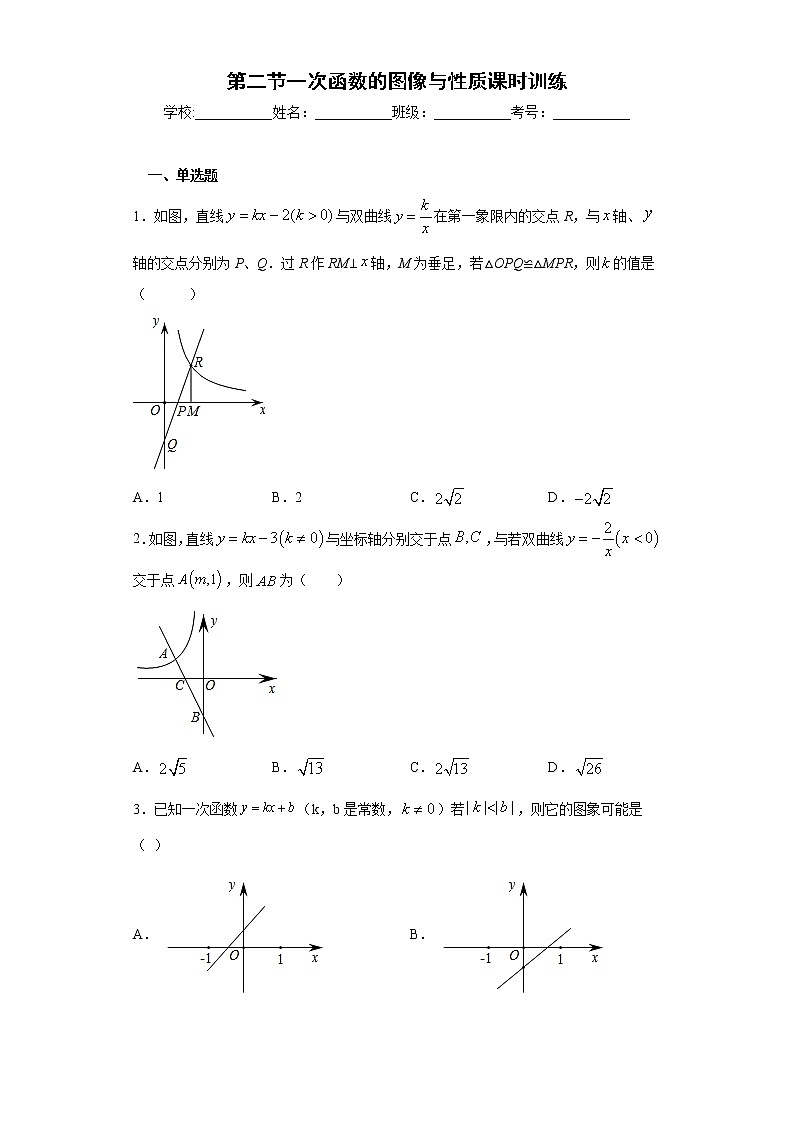
2．如图，直线与坐标轴分别交于点，与若双曲线交于点，则为（ ）
A．B．C．D．
3．已知一次函数（k，b是常数，）若，则它的图象可能是（ ）
A．B．
C．D．
4．若一次函数（k是常数，）的图象经过点P，且函数y的值随自变量x的增大而减小，则点P的坐标可以是（ ）
A．B．C．D．
5．将直线向右平移5个单位，再向上平移1个单位后，所得的直线的表达式为（ ）
A．B．C．D．
6．在平面直角坐标系中，直线与y轴的交点坐标为（ ）
A．B．C．D．
7．直线经过一、二、三象限，则直线的图象可能是图中的（ ）
A．B．C．D．
8．一次函数上有两点和，则与的大小关系是（ ）
A．B．C．D．无法比较
9．如图，已知直线与双曲线相交于和两点，则不等式的解集是（ ）
A．或B．C．或D．
10．如图，在平面直角坐标系中，点P是正比例函数y＝x图象上的一点，点A的坐标为（0，1），点B的坐标为（4，1），当PB－PA取最大值时，点P的坐标为（ ）
A．（1，2）B．（－0.5，－0.5）C．（＋3， －3）D．（－2，－2）
11．已知直线y＝x+2与函数y＝的 图象交于A，B两点（点A在点B的左边）．
（1）点A的坐标是_____；
（2）已知O是坐标原点，现把两个函数图象水平向右平移m个单位，点A，B平移后的对应点分别为A′，B′，连结OA′，OB′．当m＝_____时，|OA'﹣OB'|取最大值．
12．如图，一次函数的图象与轴交于两点，与反比例的图象交于两点，分别过两点作轴的垂线，垂足为，连接，有下列结论：①与面积相等；②；③；④．中正确的结论是______（把你认为正确结论的序号都填上）．
13．已知某直线经过点，且与两坐标轴围成的三角形的面积为2，则该直线的函数表达式是_________．
14．已知一次函数经过原点，则______．
15．如图，直线与双曲线交于两点，轴，轴与交于点，则的面积的最小值是____________．
16．将直线沿轴向上平移6个单位，所得到的直线解析式是____________．
17．在平面直角坐标系中，设一次函数，（k，b是实数，且）
（1）若函数的图象过点，求函数与x轴的交点坐标；
（2）若函数的图象经过点，求证：函数的图象经过点；
（3）若函数的图象不经过第一象限，且过点，当时，求k的取值范围．
18．在平面直角坐标系中，一次函数（k，b是常数，且）的图象经过点和．
（1）求该函数的表达式；
（2）若点在该函数的图象上，求点P的坐标；
（3）当时，求x的取值范围．
19．如图，直线与双曲线交于、两点．
（1）点坐标为 ， ， ， ．
（2）直接写出关于的不等式的解集．
20．如图，在平面直角坐标系中，点 ，把线段绕点逆时针旋转到，交轴于点，反比例函数的图象经过点．
（1）求的值；
（2）连接，若点在反比例函数的图象上，且，求点的坐标．
一、单选题
二、填空题
三、解答题
参考答案
1．C
2．A
3．D
4．C
5．B
6．C
7．C
8．A
【分析】
9．A
10．B
11．（）； 6． ．
12．①②④
13．或
14．
15．12
16．
17．（1）（-2，0）；（2）见解析；（3）
解：（1）∵函数的图象过点，
∴
∴
∴
当时，；
∴
∴函数与x轴的交点坐标为（-2，0）；
（2）∵函数的图象经过点，
∴
∴
∴；
当时，；
∴函数的图象经过点；
（3）∵函数的图象不经过第一象限，
∴；
∵的图象过点，
∴，
∴，
∵
∴，
∴．
18．（1）；（2）；（3）．
解：（1）一次函数过（2，1）和（-1,7），
∴，
解得：，
∴；
（2）由（1）可知：，
将代入，
∴，解得，
即，
∴；
（3）∵，
当时，
则，
解得：，
∴x的取值范围：．
19．（1），， ，6 （2）当时，解集为或；当时，解集为；当时，解集为或 ；当时，解集为且；当时，解集为．
解：（1）由图可得，C点的横坐标为0
将x=0代入直线方程，解得 y=1
所以C的坐标为；
将A的坐标代入直线方程得：，解得 m=2；
将B的坐标代入直线方程得：，解得 n=-2；
将A的坐标代入双曲线方程得：，解得 ；
（2）在（1）中得出，k=6；
令
去分母，化为整式并整理得：；
若且上式有解，则判别式，得
当有两个不相等解时，两个解分别为：
，
当只有唯一解时，解为：；
若无解，；
当时，图大概如下，直线和双曲线 有两个交点，也就是 有两个不相等的解 ．其中A点横坐标为，B点横坐标为 ，所求不等式的解集为 或 ；
当a=0时，图大概如下，只有一个交点，A点的横坐标为6，所求不等式的解集为；
当时，图大概如下，直线和双曲线有两个交点，也就是有两个不相等的解 ．其中A点横坐标为，B点横坐标为 ，所求不等式的解集为 或 ；
当时，图大概如下，直线和双曲线相切．交点A横坐标为，所求不等式的解集为 且；
当时，图大概如下，直线和双曲线没有交点．所求不等式的解集为；
综上，的解集是：
当时，或 ；
当时，；
当时，或 ；
当时，且；
当时，．
20．（1）3（2）
解：（1）作CE⊥x轴，垂足为E点，
∵把线段绕点逆时针旋转到，
∴∠BAC=90°，AB=AC，
∴∠CAE+∠BAO=∠CAE+∠ACE，
即∠BAO=∠ACE，
在△AOB和△CEA中，
，
∴△AOB≌△CEA（AAS），
∴OB=EA，AO=CE，
∵点，
∴EA=4，CE=3，
∴点C的坐标为(1，3)，
∵反比例函数的图象经过点，
∴k=1×3=3；
（2）设AC的解析式为y=kx+b(k≠0)，
∵点，
∴，
解得，
∴AC的解析式为，
令x=0，则y=，
∴点D的坐标为，
∵，
∴AB=，
∴S△ABC=×5×5=，
设点P坐标为，
∵，
∴，
解得，
∴点P坐标为．