2021高考数学（理）大一轮复习习题：第十二章 推理与证明、算法、复数 课时达标检测（六十二） 算法与程序框图、复数 word版含答案

这是一份2021高考数学（理）大一轮复习习题：第十二章 推理与证明、算法、复数 课时达标检测（六十二） 算法与程序框图、复数 word版含答案，共7页。


1．欧拉公式eix＝cs x＋isin x(i为虚数单位)是由瑞士著名数学家欧拉发明的，将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，在复变函数论里占有非常重要的地位，被誉为“数学中的天桥”，根据欧拉公式可知，e2i表示的复数在复平面中位于( )
A．第一象限 B．第二象限
C．第三象限 D．第四象限
解析：选B e2i＝cs 2＋isin 2，由于eq \f(π,2)<2<π，因此cs 2<0，sin 2>0，点(cs 2，sin 2)在第二象限，故选B.
2．已知eq \f(1－i2,z)＝1＋i(i为虚数单位)，则复数z＝( )
A．1＋i B．1－i C．－1＋i D．－1－i
解析：选D 由eq \f(1－i2,z)＝1＋i，得z＝eq \f(1－i2,1＋i)＝eq \f(－2i,1＋i)＝eq \f(－2i1－i,1＋i1－i)＝－1－i.
3．执行如图所示的程序框图，则可以输出函数的为( )
A．f(x)＝sin x B．f(x)＝ex
C．f(x)＝x3＋x＋2 D．f(x)＝x2
解析：选C 当输入f(x)＝sin x时，由于f(x)＝sin x是奇函数，因而输出“是奇函数”，然后结束；当输入f(x)＝ex时，f(x)＝ex不是奇函数，但恒为正，因而输出“非负”，然后结束；当输入f(x)＝x3＋x＋2时，f(x)＝x3＋x＋2既不是奇函数，又不恒为非负，因而输出该函数；而当输入f(x)＝x2时， 由于f(x)＝x2是偶函数，且非负，因而输出“非负”．故选C.
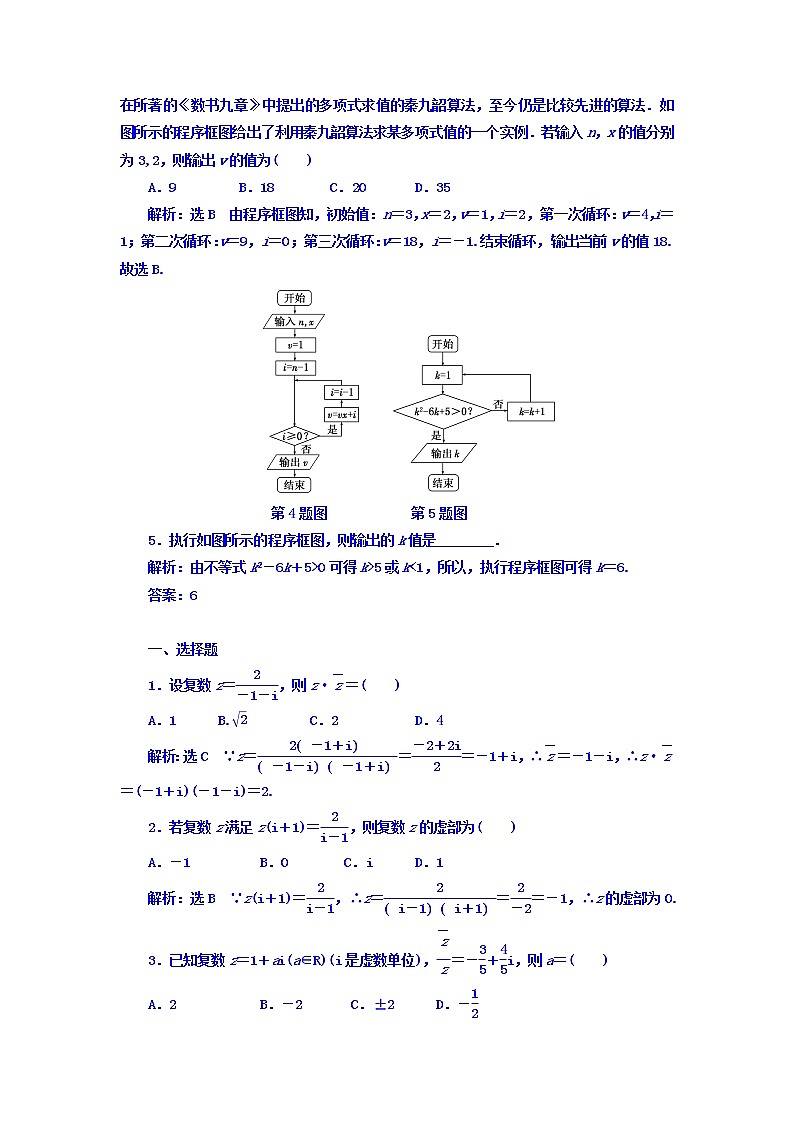
4．(2016·四川高考)秦九韶是我国南宋时期的数学家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例．若输入n，x的值分别为3,2，则输出v的值为( )
A．9 B．18 C．20 D．35
解析：选B 由程序框图知，初始值：n＝3，x＝2，v＝1，i＝2，第一次循环：v＝4，i＝1；第二次循环：v＝9，i＝0；第三次循环：v＝18，i＝－1.结束循环，输出当前v的值18.故选B.

第4题图 第5题图
5．执行如图所示的程序框图，则输出的k值是________．
解析：由不等式k2－6k＋5>0可得k>5或k<1，所以，执行程序框图可得k＝6.
答案：6
一、选择题
1．设复数z＝eq \f(2,－1－i)，则z·eq \(z,\s\up6(－))＝( )
A．1 B.eq \r(2) C．2 D．4
解析：选C ∵z＝eq \f(2－1＋i,－1－i－1＋i)＝eq \f(－2＋2i,2)＝－1＋i，∴eq \(z,\s\up6(－))＝－1－i，∴z·eq \(z,\s\up6(－))＝(－1＋i)(－1－i)＝2.
2．若复数z满足z(i＋1)＝eq \f(2,i－1)，则复数z的虚部为( )
A．－1 B．0 C．i D．1
解析：选B ∵z(i＋1)＝eq \f(2,i－1)，∴z＝eq \f(2,i－1i＋1)＝eq \f(2,－2)＝－1，∴z的虚部为0.
3．已知复数z＝1＋ai(a∈R)(i是虚数单位)，eq \f(\(z,\s\up6(－)),z)＝－eq \f(3,5)＋eq \f(4,5)i，则a＝( )
A．2 B．－2 C．±2 D．－eq \f(1,2)
解析：选B 由题意可得eq \f(1－ai,1＋ai)＝－eq \f(3,5)＋eq \f(4,5)i，即eq \f(1－ai2,1＋a2)＝eq \f(1－a2－2ai,1＋a2)＝eq \f(1－a2,1＋a2)＋eq \f(－2a,1＋a2)i＝－eq \f(3,5)＋eq \f(4,5)i，∴eq \f(1－a2,1＋a2)＝－eq \f(3,5)，eq \f(－2a,1＋a2)＝eq \f(4,5)，∴a＝－2，故选B.
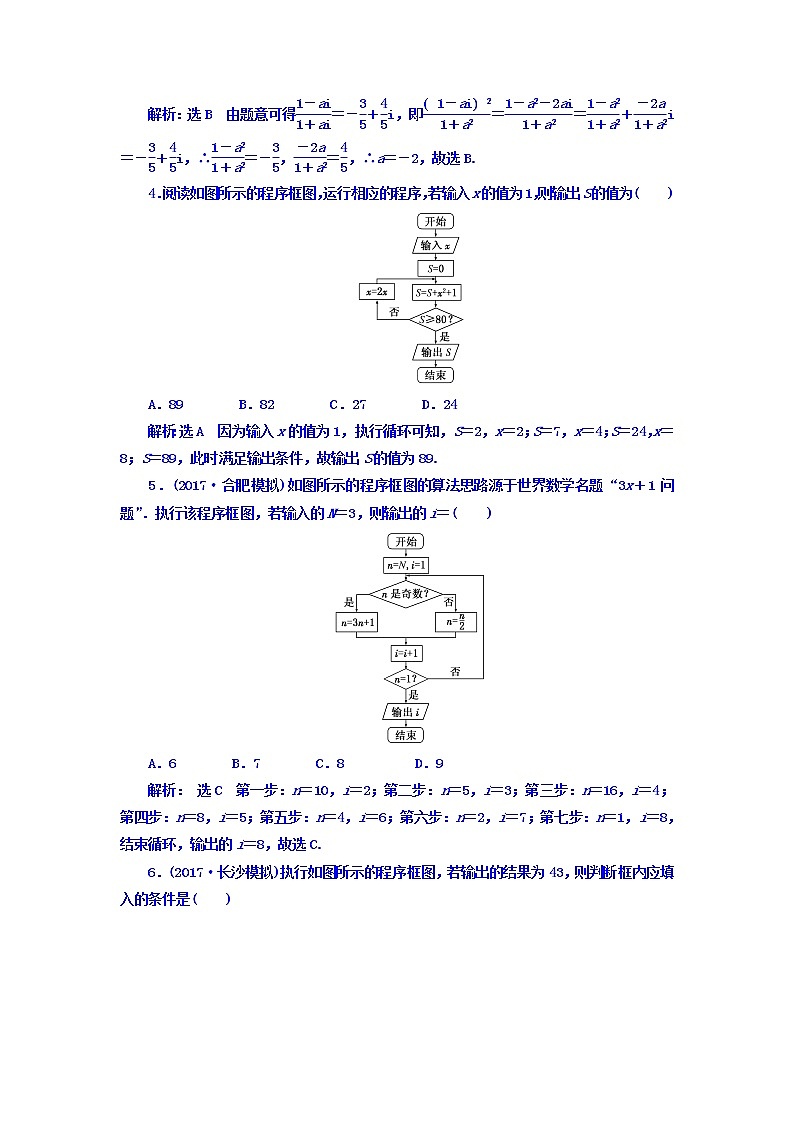
4．阅读如图所示的程序框图，运行相应的程序，若输入x的值为1，则输出S的值为( )
A．89 B．82 C．27 D．24
解析：选A 因为输入x的值为1，执行循环可知，S＝2，x＝2；S＝7，x＝4；S＝24，x＝8；S＝89，此时满足输出条件，故输出S的值为89.
5．(2017·合肥模拟)如图所示的程序框图的算法思路源于世界数学名题“3x＋1问题”．执行该程序框图，若输入的N＝3，则输出的i＝( )
A．6 B．7 C．8 D．9
解析： 选C 第一步：n＝10，i＝2；第二步：n＝5，i＝3；第三步：n＝16，i＝4；第四步：n＝8，i＝5；第五步：n＝4，i＝6；第六步：n＝2，i＝7；第七步：n＝1，i＝8，结束循环，输出的i＝8，故选C.
6．(2017·长沙模拟)执行如图所示的程序框图，若输出的结果为43，则判断框内应填入的条件是( )
A．z≤42? B．z≤20?
C．z≤50? D．z≤52?
解析：选A 运行程序：x＝0，y＝1，
因为z＝1不满足输出结果，则x＝1，y＝1；
因为z＝2×1＋1＝3不满足输出结果，则x＝1，y＝3；
因为z＝2×1＋3＝5不满足输出结果，则x＝3，y＝5；
因为z＝2×3＋5＝11不满足输出结果，则x＝5，y＝11；
因为z＝2×5＋11＝21不满足输出结果，则x＝11，y＝21；
因为z＝2×11＋21＝43满足输出结果，此时需终止循环，结合选项可知，选A.
二、填空题
7．若eq \f(3＋bi,1－i)＝a＋bi(a，b为实数，i为虚数单位)，则a＋b＝________.
解析：由eq \f(3＋bi,1－i)＝eq \f(3＋bi1＋i,1－i1＋i)＝eq \f(3－b＋3＋bi,2)＝a＋bi，
得a＝eq \f(3－b,2)，b＝eq \f(3＋b,2)，
解得b＝3，a＝0，所以a＋b＝3.
答案：3
8．复数z满足(3－4i)z＝5＋10i，则|z|＝________.
解析：由(3－4i)z＝5＋10i知，|3－4i|·|z|＝|5＋10i|，即5|z|＝5eq \r(5)，解得|z|＝eq \r(5).
答案：eq \r(5)
9．执行如图所示的程序框图，若输入n的值为8，则输出S的值为________．
解析：第一次循环：S＝2，i＝4，k＝2；
第二次循环：S＝4，i＝6，k＝3；
第三次循环：S＝8，i＝8，k＝4，当
i＝8时不满足i故输出S的值为8.
答案：8
10．执行如图所示的程序框图，则输出的实数m的值为________．
解析：分析框图可知输出的m应为满足m2≥99的最小正整数解的后一个正整数，故输出的实数m的值为11.
答案：11
三、解答题
11．计算：(1)eq \f(－1＋i2＋i,i3)；
(2)eq \f(1＋2i2＋31－i,2＋i)；
(3)eq \f(1－i,1＋i2)＋eq \f(1＋i,1－i2)；
(4)eq \f(1－\r(3)i,\r(3)＋i2).
解：(1)eq \f(－1＋i2＋i,i3)
＝eq \f(－3＋i,－i)＝eq \f(－3＋ii,－i·i)＝－1－3i.
(2)eq \f(1＋2i2＋31－i,2＋i)
＝eq \f(－3＋4i＋3－3i,2＋i)
＝eq \f(i,2＋i)＝eq \f(i2－i,5)＝eq \f(1,5)＋eq \f(2,5)i.
(3)eq \f(1－i,1＋i2)＋eq \f(1＋i,1－i2)
＝eq \f(1－i,2i)＋eq \f(1＋i,－2i)
＝eq \f(1＋i,－2)＋eq \f(－1＋i,2)＝－1.
(4)eq \f(1－\r(3)i,\r(3)＋i2)＝eq \f(\r(3)＋i－i,\r(3)＋i2)
＝eq \f(－i,\r(3)＋i)＝eq \f(－i\r(3)－i,4)
＝－eq \f(1,4)－eq \f(\r(3),4)i.
12．已知数列{an}的各项均为正数，观察程序框图，若k＝5，k＝10时，分别有S＝eq \f(5,11)和S＝eq \f(10,21)，求数列{an}的通项公式．
解：当i＝1时，a2＝a1＋d，M＝eq \f(1,a1a2)，S＝eq \f(1,a1a2)；
当i＝2时，a3＝a2＋d，M＝eq \f(1,a2a3)，S＝eq \f(1,a1a2)＋eq \f(1,a2a3)；
当i＝3时，a4＝a3＋d，M＝eq \f(1,a3a4)，S＝eq \f(1,a1a2)＋eq \f(1,a2a3)＋eq \f(1,a3a4)；
……
因此，由程序框图可知，数列{an}是等差数列，首项为a1，公差为d.
当k＝5时，S＝eq \f(1,a1a2)＋eq \f(1,a2a3)＋eq \f(1,a3a4)＋eq \f(1,a4a5)＋eq \f(1,a5a6)
＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a1)－\f(1,a2)＋\f(1,a2)－\f(1,a3)＋\f(1,a3)－\f(1,a4)＋\f(1,a4)－\f(1,a5)＋\f(1,a5)－\f(1,a6)))eq \f(1,d)
＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a1)－\f(1,a6)))eq \f(1,d)＝eq \f(5,a1a6)＝eq \f(5,11)，
∴a1a6＝11，即a1(a1＋5d)＝11.①
当k＝10时，S＝eq \f(1,a1a2)＋eq \f(1,a2a3)＋…＋eq \f(1,a10a11)
＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a1)－\f(1,a2)＋\f(1,a2)－\f(1,a3)＋…＋\f(1,a10)－\f(1,a11)))eq \f(1,d)
＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a1)－\f(1,a11)))eq \f(1,d)＝eq \f(10,a1a11)＝eq \f(10,21)，
∴a1a11＝21，即a1(a1＋10d)＝21.②
由①②解得a1＝1，d＝2.
∴an＝a1＋(n－1)d＝2n－1.