


北师大版八年级下册1 平行四边形的性质精品ppt课件
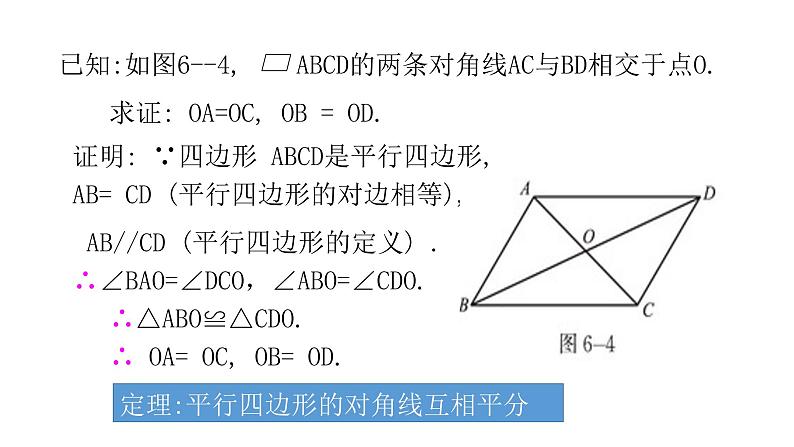
展开求证: OA=OC, OB = OD.
证明: ∵四边形 ABCD是平行四边形,AB= CD (平行四边形的对边相等),
AB//CD (平行四边形的定义) .
∴∠BAO=∠DCO,∠ABO=∠CDO.
∴△ABO≌△CDO.
∴ OA= OC, OB= OD.
已知:如图6--4, ABCD的两条对角线AC与BD相交于点O.
定理:平行四边形的对角线互相平分
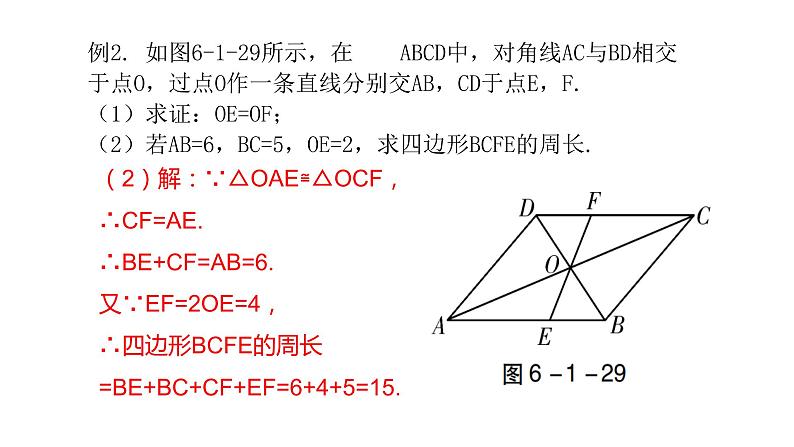
例2. 如图6-1-29所示,在 ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F. (1)求证:OE=OF;(2)若AB=6,BC=5,OE=2,求四边形BCFE的周长.
(1)证明:在 ABCD中,∵AC与BD相交于点O,∴OA=OC,AB∥CD. ∴∠OAE=∠OCF. 在△OAE和△OCF中,∠OAE=∠OCF, OA=OC, ∠AOE=∠COF,∴△OAE≌△OCF(ASA). ∴OE=OF.
(2)解:∵△OAE≌△OCF,∴CF=AE. ∴BE+CF=AB=6. 又∵EF=2OE=4,∴四边形BCFE的周长=BE+BC+CF+EF=6+4+5=15.
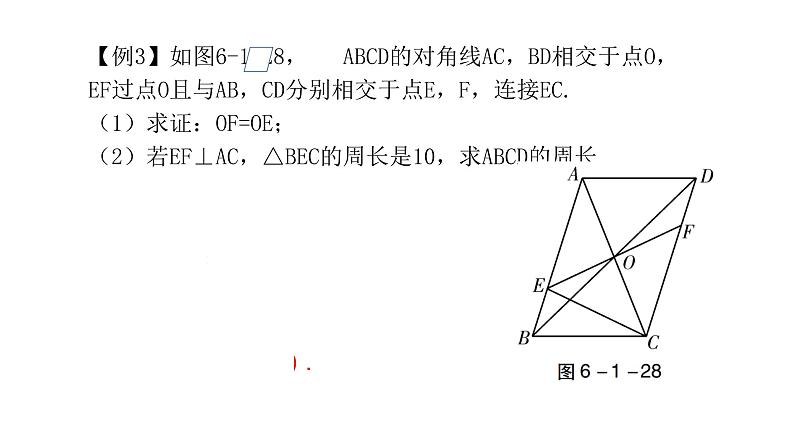
【例3】如图6-1-28, ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接EC.(1)求证:OF=OE;(2)若EF⊥AC,△BEC的周长是10,求ABCD的周长.
(1)证明:∵四边形ABCD是平行四边形,∴OD=OB,DC∥AB.∴∠FDO=∠EBO.在△DFO和△BEO中,∠FDO=∠EBO, OD=OB, ∠FOD=∠EOB,∴△DFO≌△BEO(ASA).∴OF=OE.
(2)解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OA=OC.∵EF⊥AC,∴AE=CE.∵△BEC的周长是10,∴BC+BE+CE=BC+BE+AE=BC+AB=10.∴ ABCD的周长=2(BC+AB)=20.
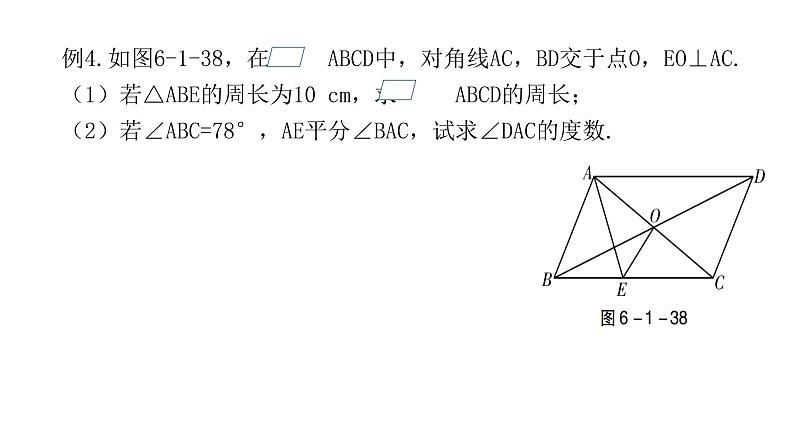
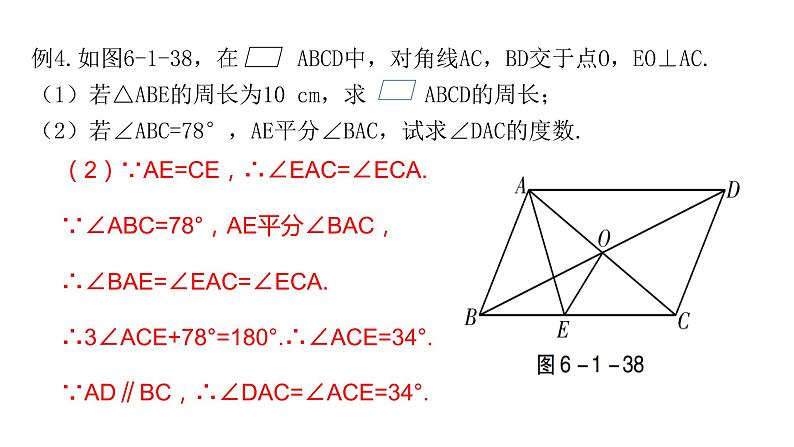
例4.如图6-1-38,在 ABCD中,对角线AC,BD交于点O,EO⊥AC. (1)若△ABE的周长为10 cm,求 ABCD的周长;(2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数.
解:(1)∵四边形ABCD是平行四边形, ∴OA=OC. ∵OE⊥AC, ∴AE=CE. 故△ABE的周长=AB+BE+AE=AB+BC=10(cm).根据平行四边形的对边相等,得 ABCD的周长为2×10=20(cm).
(2)∵AE=CE,∴∠EAC=∠ECA.∵∠ABC=78°,AE平分∠BAC,∴∠BAE=∠EAC=∠ECA.∴3∠ACE+78°=180°.∴∠ACE=34°.∵AD∥BC,∴∠DAC=∠ACE=34°.
1.如图6-1-18,在平行四边形ABCD中,BE⊥AC,垂足E在CA的延长线上,DF⊥AC,垂足F在AC的延长线上,求证:AE=CF.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD. ∴∠BAC=∠DCA. ∴180°-∠BAC=180°-∠DCA, 即∠EAB=∠FCD. ∵BE⊥AC,DF⊥AC,∴∠BEA=∠DFC=90°. 在△BEA和△DFC中, ∴△BEA≌△DFC(AAS). ∴AE=CF.
∠BEA=∠DFC∠EAB=∠FCDAB=CD
2. 如图6-1-19,在 ABCD中,E是BC边上一点,连接DE,使得DE=AD,作∠DAF=∠CDE.求证:(1)△DAF≌△EDC;(2)AE平分∠BAF.
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC. ∴∠ADE=∠DEC. 在△DAF和△EDC中,∴△DAF≌△EDC(ASA).
∠DEA=∠EDCAD=DE∠ADF=∠DEC
(2)∵△DAF≌△EDC,∴∠AFD=∠C. ∵DE=AD,∴∠AEF=∠DAE. ∵四边形ABCD是平行四边形,∴AD∥BC,∠DAE=∠AEB,∠B+∠C=180°.∴∠AEB=∠AEF. ∵∠AFE+∠AFD=180°,∴∠B=∠AFE. 在△BAE和△FAE中,
∴△BAE≌△FAE(AAS).
∴∠BAE=∠FAE,即AE平分∠BAF.
∠B=AFE∠AEB=AEFAE=AE
3. 如图6-1-20,在 ABCD中,AP和BP分别平分∠DAB和∠CBA,PQ∥AD,若AD=5 cm,AP=8 cm,求△ABP的面积.
解: ∵四边形ABCD是平行四边形,∴AD//CB.
∴∠DAB+∠CBA=180°.
又∵AP和BP分别平分∠DAB和∠CBA.
在△APB中,∠APB=180°-(∠PAB+∠PBA)=90°.
∵AP平分∠DAB,∴∠DAP=∠PAB.
∵AB//CD,∴∠PAB=D∠PA.
∴∠DAP=∠DPA. ∴△ADP是等腰三角形.
∴AD=DP=5(cm).
4. 如图6-1-36,在 ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD,CD于点F,G. 求证:△ADB≌△CEA.
证明:∵四边形ABCD是平行四边形,∴AD=BC,∠ABC+∠BAD=180°.又∵AB=AC,∴∠ABC=∠ACB. ∵∠ACB+∠ACE=180°,∴∠BAD=∠ACE. ∵CE=BC,∴CE=AD,在△ADB和△CEA中,AD=CE,∠BAD=∠ACE,AB=CA,∴△ADB≌△CEA(SAS).
5. 如图6-1-37,在 ABCD中,AB=5,AC=4,AD=3. (1)求 ABCD的面积;(2)求BD的长.
6. 如图6-1-39,在 ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于点F. (1)求证:CF=CD;(2)若AF平分∠BAD,连接DE,试判断DE与AF的位置关系,并说明理由.
在△BAE和△CFE中,∠BAE=∠CFE, ∠EBA=∠ECF, BE=CE,
∴AB∥CD,AB=CD.
(1)证明:∵四边形ABCD是平行四边形,
∵点F为DC的延长线上的一点,
∴∠BAE=∠CFE,∠ECF=∠EBA.
∵E为BC的中点,∴BE=CE.
∴△BAE≌△CFE(AAS).
∴BA=CF. ∴CF=CD.
初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质教学课件ppt: 这是一份初中数学北师大版八年级下册第六章 平行四边形1 平行四边形的性质教学课件ppt,文件包含北师大版数学八年级下册61平行四边形的性质第2课时同步课件pptx、北师大版数学八年级下册61平行四边形的性质第2课时教学设计含教学反思docx等2份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
北师大版八年级下册1 平行四边形的性质图文课件ppt: 这是一份北师大版八年级下册1 平行四边形的性质图文课件ppt,共14页。PPT课件主要包含了讲授新课,课堂练习,课时小结,教材习题62,课后作业等内容,欢迎下载使用。
数学八年级下册第六章 平行四边形1 平行四边形的性质精品课件ppt: 这是一份数学八年级下册第六章 平行四边形1 平行四边形的性质精品课件ppt,文件包含北师大版数学八年级下册61平行四边形的性质第2课时课件PPTppt、北师大版数学八年级下册61平行四边形的性质第2课时教案doc等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。













