中考冲刺集训--矩形、菱形、正方形测试题(含解析)

中考冲刺集训--矩形、菱形、正方形

(时间：60分钟　满分：70分)

一、选择题(本大题共7小题，每小题3分，共21分)

1．(2019无锡)下列结论中，矩形具有而菱形不一定具有的性质是(　　)

A. 内角和为360°　　　　　　　　　　　B. 对角线互相平分

C. 对角线相等                        D. 对角线互相垂直

2．(2019娄底)顺次连接菱形四边中点得到的四边形是(　　)

A. 平行四边形　　　　B. 菱形　　　　　C. 矩形　　　　　D. 正方形

3．(2019天津)如图，四边形ABCD为菱形，A，B两点的坐标分别是(2，0)，(0，1)，点C，D在坐标轴上，则菱形ABCD的周长等于(　　)

A.              B. 4             C. 4             D. 20

第3题图

4．(2019孝感)如图，在正方形ABCD中，点E、F分别在边CD、AD上，BE与CF交于点G.若BC＝4，DE＝AF＝1，则FG的长为(　　)

A.           B.           C.          D.

第4题图

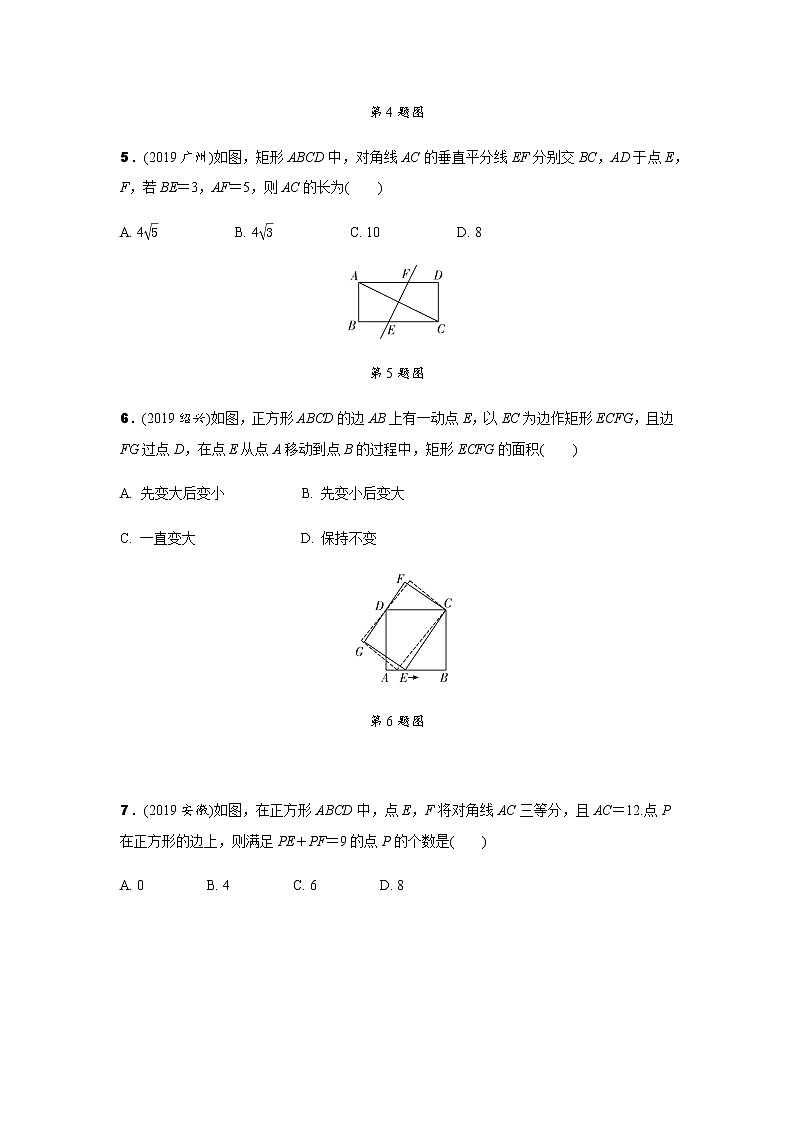
5．(2019广州)如图，矩形ABCD中，对角线AC的垂直平分线EF分别交BC，AD于点E，F，若BE＝3，AF＝5，则AC的长为(　　)

A. 4           B. 4           C. 10           D. 8

第5题图　

6．(2019绍兴)如图，正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D，在点E从点A移动到点B的过程中，矩形ECFG的面积(　　)

A. 先变大后变小           B. 先变小后变大

C. 一直变大               D. 保持不变

第6题图

7．(2019安徽)如图，在正方形ABCD中，点E，F将对角线AC三等分，且AC＝12.点P在正方形的边上，则满足PE＋PF＝9的点P的个数是(　　)

A. 0         B. 4         C. 6         D. 8

第7题图

二、填空题(本大题共5小题，每小题3分，共15分)

8．(2019扬州)将一个矩形纸片折叠成如图所示的图形，若∠ABC＝26°，则∠ACD＝________°.

第8题图

9．(2019呼和浩特)已知正方形ABCD的面积是2，E为正方形一边BC从B到C方向的延长线上的一点，若CE＝，连接AE，与正方形另一边CD交于点F，连接BF并延长，与线段DE交于点G，则BG的长为________．

10．(2019温州)三个形状大小相同的菱形按如图所示方式摆放，已知∠AOB＝∠AOE＝90°，菱形的较短对角线长为2 cm，若点C落在AH的延长线上，则△ABE的周长为________cm.

第10题图

11．(2019贵阳)如图，在矩形ABCD中，AB＝4，∠DCA＝30°，点F是对角线AC上的一个动点，连接DF，以DF为斜边作∠DFE＝30°的直角三角形DEF，使点E和点A位于DF两侧，点F从点A到点C的运动过程中，点E的运动路径长是________．

第11题图

12．如图，正方形ABCD的边长为a，点E在边AB上运动(不与点A，B重合)，∠DAM＝45°，点F在射线AM上，且AF＝BE，CF与AD相交于点G，连接EC，EF，EG.则下列结论：①∠ECF＝45°；②△AEG的周长为(1＋)a；③BE2＋DG2＝EG2；④△EAF的面积的最大值是a2.

其中正确的结论是________．(填写所有正确结论的序号)

第12题图

三、解答题(本大题共4小题，13～15题每题8分，16题10分，共34分)

13．(2019青岛)如图，在□ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG＝AE，连接CG.

(1)求证：△ABE≌△CDF；

(2)当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．

第13题图

14．(2019德阳)如图，在四边形ABCD中，BC∥AD，BC＝AD，点E为AD的中点，点F为AE的中点，AC⊥CD，连接BE，CE，CF.

(1)判断四边形ABCE的形状，并说明理由；

(2)如果AB＝4，∠D＝30°，点P为BE上的动点，求△PAF的周长的最小值．

第14题图

15．(2019百色)如图，菱形ABCD中，作BE⊥AD、CF⊥AB，分别交AD、AB的延长线于点E、F.

(1)求证：AE＝BF；

(2)若点E恰好是AD的中点，AB＝2，求BD的值．

第15题图

16．(2019海南)如图，在边长为1的正方形ABCD中，E是边CD的中点，点P是边AD上一点(与点A、D不重合)，射线PE与BC的延长线交于点Q.

(1)求证：△PDE≌△QCE；

(2)过点E作EF∥BC交PB于点F，连接AF，当PB＝PQ时，

①求证：四边形AFEP是平行四边形；

②请判断四边形AFEP是否为菱形，并说明理由．

第16题图

中考冲刺集训

1．C　2.C　3.C　4.A　5.A　6.D　7.D　8．128　9.　10.12＋8　11.　12.①④

13．(1)证明：∵四边形ABCD是平行四边形，

∴OB＝OD，AB＝CD.··········(1分)

∵AB∥CD，

∴∠ABE＝∠CDF.··········(2分)

∵点E，F分别为OB，OD的中点，

∴BE＝OB，DF＝OD.··········(3分)

∴BE＝DF.

∴△ABE≌△CDF(SAS)．··········(4分)

(2)解：当AB＝AC时，四边形EGCF是矩形．··········(6分)

理由：∵AB＝AC，AO＝OC，

∴AB＝AO.

∵BE＝OE，

∴AE⊥BO(等腰三角形三线合一)．··········(7分)

∴∠FEG＝90°.

由(1)得△ABE≌△CDF，

∴∠AEB＝∠CFD＝90°，AE＝CF.

∵∠AEB＝∠FEG，

∴∠CFD＝∠FEG.

∴EG∥FC.

∵AE＝CF，EG＝AE，

∴EG＝CF，

∴四边形EGCF是平行四边形．

又∵∠FEG＝90°，

∴四边形EGCF是矩形．··········(8分)

14．解：(1)四边形ABCE是菱形．理由如下：

∵BC＝AD，点E为AD的中点，

∴BC＝AE＝ED.··········(1分)

又∵BC∥AD，

∴四边形ABCE为平行四边形，四边形BCDE为平行四边形．

∴BE∥CD.

又∵AC⊥CD，

∴AC⊥BE.

∴四边形ABCE为菱形；··········(3分)

(2)∵∠D＝30°，AC⊥CD，

∴∠EAC＝∠ACE＝60°.

∴△AEC为等边三角形．

∵四边形ABCE为菱形，

∴EC＝AE＝AB＝4.

又∵点A与点C关于对角线BE对称，

∴PA＝PC.··········(5分)

当点P运动到FC与BE的交点处为△PAF周长最小值的位置，

∴此时△PAF的周长＝PA＋PF＋AF＝PC＋PF＋AF＝FC＋AF.

∵△AEC为等边三角形，

∴FC＝2 ，AF＝AE＝2.··········(7分)

∴△PAF的周长最小值为2＋2 .··········(8分)

15．(1)证明：∵四边形ABCD是菱形，

∴AD∥BC，

∴∠BAE＝∠CBF.··········(1分)

∵BE⊥AD，CF⊥AB，

∴∠AEB＝∠BFC.··········(2分)

又∵AB＝BC，

∴△ABE≌△BCF(AAS)．

∴AE＝BF.··········(4分)

(2)解：由题意知，BE垂直平分AD，即BE是AD的垂直平分线，

∴点B到AD两边的距离相等．··········(6分)

∴BD＝AB＝2.(8分)

16．(1)证明：∵四边形ABCD是正方形，

∴∠D＝∠BCD＝90°.

∴∠ECQ＝90°＝∠D.··········(1分)

∵E是CD的中点，

∴DE＝CE.··········(2分)

又∵∠DEP＝∠CEQ，

∴△PDE≌△QCE.··········(3分)

(2)①证明：如解图，由(1)可知△PDE≌△QCE，

∴PE＝QE＝PQ.

又∵EF∥BC，

∴PF＝FB＝PB.

∵PB＝PQ，

∴PF＝PE.

∴∠1＝∠2.

∵四边形ABCD是正方形，

∴∠BAD＝90°.

在Rt△ABP中，F是PB的中点，

∴AF＝BP＝FP.

∴∠3＝∠4.

又∵AD∥EF，

∴∠1＝∠4.

∴∠2＝∠3.

又∵PF＝FP，

∴△APF≌△EFP.

∴AP＝EF.

∴四边形AFEP是平行四边形．··········(6分)

②解：四边形AFEP不是菱形，理由如下：

第16题解图

设PD＝x，则AP＝1－x，

由(1)可知△PDE≌△QCE，

∴CQ＝PD＝x.

∴BQ＝BC＋CQ＝1＋x.

∵点E，F分别是PQ，PB的中点，

∴EF＝BQ＝，

由①可知AP＝EF，

即1－x＝，解得x＝，

∴PD＝，AP＝.

在Rt△PDE中，DE＝，

∴PE＝＝.

∴AP≠PE.

∴四边形AFEP不是菱形．··········(10分)