第八单元 第27课时 平行四边形（含答案）

这是一份第八单元 第27课时 平行四边形（含答案），共34页。PPT课件主要包含了小题热身，图27－1，图27－2，图27－3，考点管理，互相平分，图27－4，图27－5，图27－6，图27－7等内容，欢迎下载使用。

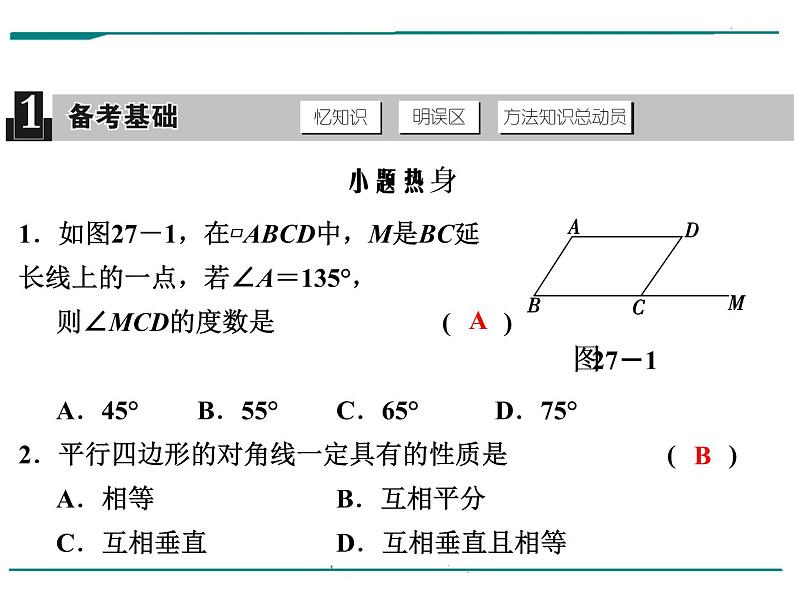
1．如图27－1，在▱ABCD中，M是BC延长线上的一点，若∠A＝135°，则∠MCD的度数是 (　　)A．45° B．55° C．65° D．75°2．平行四边形的对角线一定具有的性质是 (　　)A．相等 B．互相平分C．互相垂直 D．互相垂直且相等
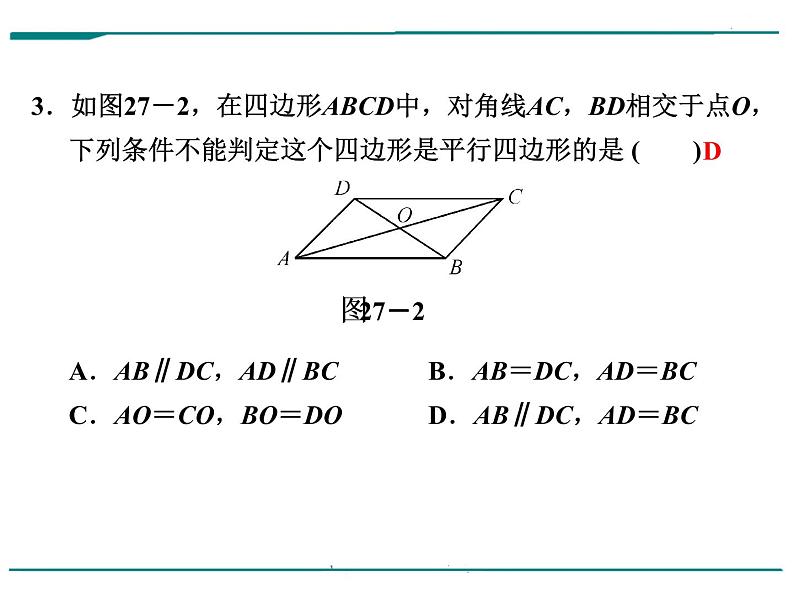
3．如图27－2，在四边形ABCD中，对角线AC，BD相交于点O，下列条件不能判定这个四边形是平行四边形的是 (　　)A．AB∥DC，AD∥BC B．AB＝DC，AD＝BCC．AO＝CO，BO＝DO D．AB∥DC，AD＝BC
【解析】 A．由AB∥DC，AD∥BC可知，四边形ABCD的两组对边互相平行，则该四边形是平行四边形；B.由AB＝DC，AD＝BC可知，四边形ABCD的两组对边相等，则该四边形是平行四边形；C.由AO＝CO，BO＝DO可知，四边形ABCD的两条对角线互相平分，则该四边形是平行四边形；D.由AB∥DC，AD＝BC可知，四边形ABCD的一组对边平行，另一组对边相等，据此不能判定该四边形是平行四边形，故本选项符合题意．故选D.
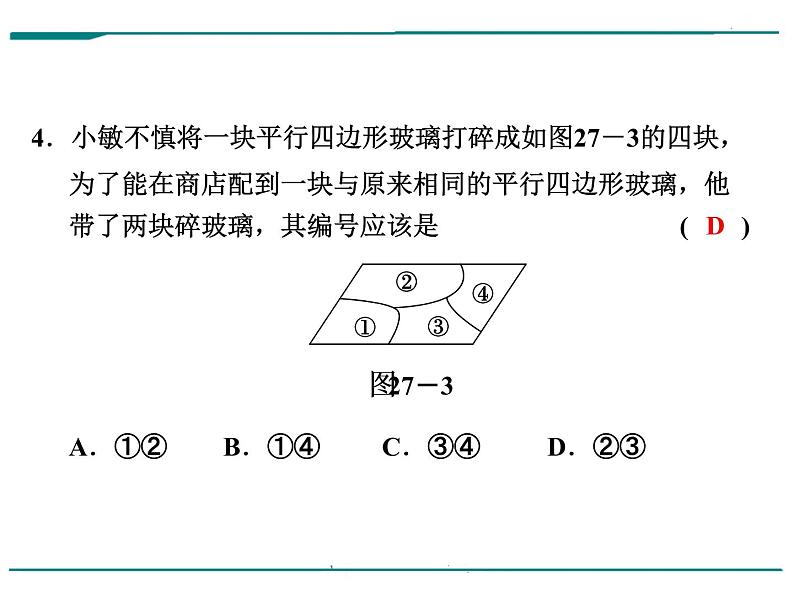
4．小敏不慎将一块平行四边形玻璃打碎成如图27－3的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是 (　　)A．①② B．①④ C．③④ D．②③
5．在▱ABCD中，∠B ＋∠D＝200°，则∠A＝____．【解析】 根据“平行四边形的对角相等、邻角互补”可以求得∠A＝180°－200°÷2＝80°.
一、必知3 知识点1．平行四边形的定义和性质定义：两组对边分别_____的四边形是平行四边形．性质定理：(1)平行四边形的对角_____ ；(2)平行四边形的对边_____ ；(3)平行四边形的对角线互相_____ ．推论：(1)夹在两条平行线间的平行线段相等；(2)夹在两条平行线间的垂线段相等．
【智慧锦囊】(1)平行四边形是中心对称图形，它的对称中心是两条对角线的交点；(2)若一条直线过平行四边形的对角线的交点，那么这条直线被一组对边截下的线段以对角线的交点为对称中心，且这条直线等分平行四边形的面积．
2．平行四边形的判定判定定理：(1)一组对边平行且_____的四边形是平行四边形；(2)两组对边分别_____的四边形是平行四边形；(3)对角线_________的四边形是平行四边形；(4)两组对角分别_____的四边形是平行四边形．3．平行四边形的面积平行四边形的面积：平行四边形的面积＝底×高．注意：同底(等底)同高(等高)的平行四边形面积_____ ．
二、必会2 方法1．平行四边形的判定方法(1)若条件中涉及角，试着用“两组对角分别相等”来证明；(2)若条件中涉及对角线，试着用“对角线互相平分”来证明；(3)若条件中涉及边，试着用“两组对边分别平行”，“两组对边分别相等”或“一组对边平行且相等”来证明．
2．平行四边形中常用的辅助线的作法(1)连对角线把平行四边形问题转化为全等三角形问题；(2)有平行线时，作平行线构造平行四边形；(3)有中点时，作加倍中线构造平行四边形； (4)图形具有邻边特征时(如等腰三角形，等边三角形等)，可以通过引辅助线把图形的某一部分绕邻边的公共端点旋转到另一位置．
平行四边形的性质如图27－4，E是▱ABCD的边AD的中点，连结CE并延长交BA的延长线于F，若CD＝6，求BF的长．【解析】 由平行四边形的性质得出AB＝CD＝6，AB∥CD，由平行线的性质得出∠F＝∠DCE，由AAS证明△AEF≌△DEC，得出AF＝CD＝6，即可求出BF的长．
解：∵E是▱ABCD的边AD的中点，∴AE＝DE，∵四边形ABCD是平行四边形，∴AB＝CD＝6，AB∥CD，∴∠F＝∠DCE，
1．如图27－5，在▱ABCD中，AB＝6，BC＝8，∠BCD的平分线交AD于点E，交BA的延长线于点F，则AE＋AF的值等于 (　　)A．2 B．3C．4 D．6
【解析】 ∵四边形ABCD是平行四边形，∴AB∥CD，AD＝BC＝8，CD＝AB＝6，∴∠F＝∠DCF，∵CF为∠BCD的平分线，∴∠FCB＝∠DCF，∴∠F＝∠FCB，∴BF＝BC＝8，同理：DE＝CD＝6，∴AF＝BF－AB＝2，AE＝AD－DE＝2，∴AE＋AF＝4.
2．如图27－6，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F.(1)求证：△ADE≌△FCE；(2)若∠BAF＝90°，BC＝5，EF＝3，求CD的长．【解析】 (1)由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE＝∠F，∠D＝∠ECF，由AAS证明△ADE≌△FCE；(2)由全等三角形的性质得出AE＝EF＝3，由平行线的性质证出∠AED＝∠BAF＝90°，由勾股定理求出DE，即可得出CD的长．
解：(1)证明：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAE＝∠F，∠D＝∠ECF，∵E是CD的中点，∴DE＝CE，在△ADE和△FCE中，
(2)∵△ADE≌△FCE，∴AE＝EF＝3，∵AB∥CD，∴∠AED＝∠BAF＝90°，∵在▱ABCD中，AD＝BC＝5，
3．如图27－7，在▱ABCD中，DE＝CE，连结AE并延长交BC的延长线于点F.(1)求证：△ADE≌△FCE；(2)若AB＝2BC，∠F＝36°.求∠B的度数．解： (1)证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴∠D＝∠ECF，
∴△ADE≌△FCE(ASA)；(2)∵△ADE≌△FCE，∴AD＝FC，∵AD＝BC，AB＝2BC，∴AB＝FB，∴∠BAF＝∠F＝36°，∴∠B＝180°－2×36°＝108°.【点悟】　平行四边形的对边的相等且平行，角的相等或互补，对角线的互相平分，面积公式，中心对称等性质，为我们解决相关问题提供了直接根据，创造了有利条件，熟记这些性质，对解题尤为重要．
平行四边形的判定 如图27－8，在四边形ABCD中，AD＝BC，BE＝DF，AE⊥BD，CF⊥BD，垂足分别为E，F.(1)求证：△ADE≌△CBF；(2)若AC与BD相交于点O，求证：AO＝CO.
∴Rt△ADE≌Rt△CBF(HL)；(2)∵Rt△ADE≌Rt△CBF，∴∠ADE＝∠CBF，∴AD∥BC，又∵AD＝BC，∴四边形ABCD是平行四边形，∴AO＝CO.
1．如图27－9，点B，E，C，F在一条直线上，AB＝DF，AC＝DE，BE＝FC.(1)求证：△ABC≌△DFE；(2)连结AF，BD，求证：四边形ABDF是平行四边形．
∴△ABC≌△DFE(SSS)；(2)连结AF，BD，如答图所示：由(1)知△ABC≌△DFE，∴∠ABC＝∠DFE，∴AB∥DF，∵AB＝DF，∴四边形ABDF是平行四边形．
2．嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图27－10的四边形ABCD，并写出了如下不完整的已知和求证．已知：如图27－10，在四边形ABCD中，BC＝AD，AB＝____．求证：四边形ABCD是_____四边形．(1)在横线上填空，以补全已知和求证；(2)按嘉淇的想法写出证明；(3)用文字叙述所证命题的逆命题为_____________________ _________ ．
解：(2)证明：如答图，连结BD，在△ABD和△CDB中，
∴△ABD≌△CDB(SSS)，∴∠ADB＝∠CBD，∠ABD＝∠CDB，∴AD∥CB，AB∥CD，∴四边形ABCD是平行四边形．
平行四边形的开放与探究 如图27－11，在四边形ABCD中，对角线AC与BD相交于点O，在①AB∥CD；②AO＝CO；③AD＝BC中任意选取两个作为条件，“四边形ABCD是平行四边形”作为结论构成命题．(1)以①②作为条件构成的命题是真命题吗？若是，请证明；若不是，请举出反例；(2)写出按题意构成的所有命题中的假命题，并举出反例加以说明(命题请写成“如果……，那么……”的形式)．
解： (1)是真命题．证明：∵AB∥CD，∴∠ABO＝∠CDO.又∵∠AOB＝∠COD，AO＝CO，∴△ABO≌△CDO(AAS)，∴AB＝CD，∴四边形ABCD是平行四边形；(2)假命题：①在四边形ABCD中，如果AB∥CD，AD＝BC，那么四边形ABCD是平行四边形；②在四边形ABCD中，如果AO＝CO，AD＝BC，那么四边形ABCD是平行四边形．
反例：如答图①，在四边形ABCD中，AB∥CD，AD＝BC，但四边形ABCD不是．平行四边形；如答图②，在四边形ABCD中，AO＝CO，AD＝BC，但四边形ABCD不是平行四边形
如图27－12，请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并证明(写出一种即可)．关系：①AD∥BC，②AB＝CD，③∠A＝∠C，④∠B＋∠C＝180°.已知：在四边形ABCD中，___________，___________ ．求证：四边形ABCD是平行四边形．
【解析】 选用的条件应符合平行四边形的定义或判定定理所需的条件．解：答案不唯一，如：求证：四边形ABCD是平行四边形．证明：∵AD∥BC，∴∠A＋∠B＝180°.∵∠A＝∠C，∴∠B＋∠C＝180°.∴AB∥CD，∴四边形ABCD是平行四边形．【点悟】　熟练掌握平行四边形的判定是解决此类问题的关键．
必明2 易错点1．平行四边形的性质常用于证明线段相等，角相等或计算边长和角度等，在应用时注意分清对边、邻边、对角、邻角等．2．一组对边相等，一组对角相等的四边形不一定是平行四边形．反例如下：如图27－13，△ABE是等腰三角形，作△DCA≌△EAC，所以∠B＝∠E＝∠D，AB＝AE＝DC，显然，四边形ABCD不是平行四边形．