






第七单元 第25课时 尺规作图(含答案)
展开1.如图25-1,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,那么第二步的作图痕迹②的作法是 ( )A.以点F为圆心,OE长为半径画弧B.以点F为圆心,EF长为半径画弧C.以点E为圆心,OE长为半径画弧D.以点E为圆心,EF长为半径画弧
【解析】 用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,第二步的作图痕迹②的作法是以点E为圆心,EF长为半径画弧.
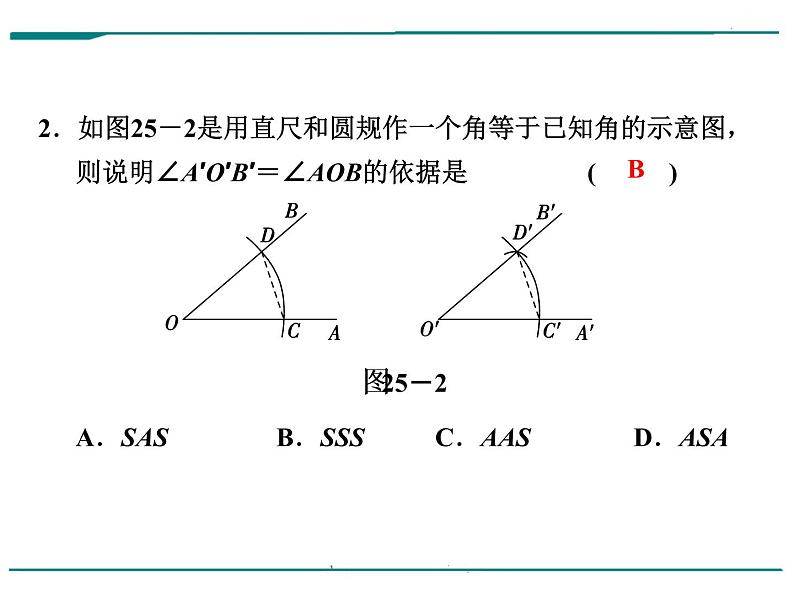
2.如图25-2是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是 ( ) A.SAS B.SSS C.AAS D.ASA
A.①②③ B.①②④C.①③④ D.②③④
一、必知3 知识点1.尺规作图尺规作图:在几何里,把限定用没有刻度的直尺和圆规来画图称为尺规作图.五种基本作图:(1)作一条线段等于已知线段;(2)作一个角等于已知角;(3)作一个角的平分线;(4)作线段的垂直平分线;(5)过定点作已知直线的垂线.
2.利用尺规作三角形(1)已知三角形的三边,求作三角形;(2)已知三角形的两边及其夹角,求作三角形;(3)已知三角形的两角及其夹边,求作三角形;(4)已知三角形的两角及其中一角的对边,求作三角形;(5)已知直角三角形一直角边和斜边,求作直角三角形.3.过点作圆过一个点可以作无数个圆;经过两点可以作无数个圆,这些圆的圆心在连结这两点的线段的垂直平分线上;过不在同一直线上的三点可以作一个圆.
二、必会2 方法1.尺规作图的关键(1)先分析题目,读懂题意,判断题目要求作什么;(2)读懂题意后,再运用几种基本作图方法解决问题. 2.根据已知条件作等腰三角形或直角三角形求作三角形的关键是确定三角形的三个顶点,作图依据是三角形全等的判定,常借助基本作图来完成,如作直角三角形就先作一个直角.
基本作图 下列四种基本尺规作图分别表示①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点作已知直线的垂线.则对应选项中作法错误的是 ( )A.① B.②C.③ D.④
【解析】 ①利用有三条边对应相等的两个三角形全等及全等三角形对应角相等可作一个角等于已知角;②利用有三条边对应相等的两个三角形全等及全等三角形对应角相等可作一个角的平分线;③根据到线段两端点距离相等的点在线段的垂直平分线上及两点确定一条直线可作已知线段的垂直平分线,但是这里只确定了一个点,不能确定直线,③错误;④根据到线段两端点距离相等的点在线段的垂直平分线上及两点确定一条直线可过直线外一点作已知直线的垂线.
1.[2017·邵阳]如图25-4所示,已知∠AOB=40°,现按照以下步骤作图:①在OA,OB上分别截取线段OD,OE,使OD=OE;
2.如图25-5,在△ABC中,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)连结AD,若∠B=37°,求∠CAD的度数.
解: (1)点D的位置如答图所示(D为AB垂直平分线与BC的交点);(2)在Rt△ABC中,∵∠B=37°,∴∠CAB=53°.又∵AD=BD,∴∠BAD=∠B=37°.∴∠CAD=∠CAB-∠BAD=16°.
3.如图25-6,已知△ABC.(1)作∠BAC的平分线交BC于点D(要求尺规作图,保留作图痕迹,不写作法);(2)若AB=AC=5,BC=6,求AD的长.
解: (1)如答图所示,AD即为所求;(2)∵AB=AC=5,AD平分∠BAC,【点悟】 本题考查了线段垂直平分线的作法以及线段垂直平分线上的点到线段两端点的距离相等的性质.
利用尺规作三角形 已知:如图25-7,线段a,c,∠α.求作:△ABC,使BC=a,AB=c,∠ABC=∠α.【解析】 先画出与α相等的角,再画出a,c的长,连结AC,则△ABC即为所求作的三角形.
解:①如答图①,以α的顶点B′为圆心,任意长为半径画弧,交α的两边于点A′,C′;②如答图②,作射线BH,以B为圆心,以B′C′为半径画弧,交BH于点F,以F为圆心,C′A′长为半径画弧,两弧交于点E,连结BE;
③以B为圆心,a为半径画弧交射线BH于点C,以B为圆心,c为半径画弧交BE的延长线于点A,连结AC,则△ABC即为所求作的三角形. ① ②
用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:如图25-8,线段c,直线l及l外一点A.求作:Rt△ABC,使直角边为AC(AC⊥l,垂足为C),斜边AB=c.
解: 如答图,Rt△ABC即为所求. 【点悟】 利用尺规作图一般的作法是先分析题目,再作出图形;作直角、中点和角平分线等要保留作图痕迹.
尺规作图与几何证明的综合运用 如图25-9,已知△ABC,∠B=40°.(1)在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);(2)连结EF,DF,求∠EFD的度数.
例3答图【解析】 (1)因为内切圆圆心到三角形三边的距离相等,到角两边距离相等的点在角的平分线上,所以要确定三角形的内心,首先要作出三角形两个内角的平分线,其交点即为所求的内切圆圆心O,再过点O作三角形一边的垂线,以点O为圆心,垂线段为半径作圆,即为内切圆,圆与三角形另两边的交点即为切点;
(2)连结OD,OE,构造四边形BDOE,根据切线的性质,可得∠ODB=∠OEB=90°,由四边形内角和求得∠DOE的度数,再根据圆心角与圆周角的关系求得∠EFD.解:(1)如答图,⊙O即为所求;(2)连结OD,OE,则OD⊥AB,OE⊥BC,∴∠ODB=∠OEB=90°,又∵∠B=40°,∴∠DOE=140°,∴∠EFD=70°.
如图25-10,在△ABC中,∠B=90°.(1)尺规作图:按下列要求完成作图,保留作图痕迹,并标明字母:①作线段AC的垂直平分线l,交AC于点O;②连结BO并延长,在BO的延长线上截取OD,使得OD=OB;③连结DA,DC.(2)判断四边形ABCD的形状,并说明理由.
变式跟进答图【解析】 (1)①利用线段垂直平分线的作法得出即可;②利用射线的作法得出点D位置;③连结DA,DC即可;(2)利用直角三角形斜边与其边上中线的关系可得出AO=CO=BO=DO,进而得出答案.
解:(1)如答图所示;(2)四边形ABCD是矩形.理由:
必明2 易错点1.尺规作图的工具是没有刻度的直尺和圆规,注意要求是没有刻度,不能用刻度尺去作线段或用量角器作直角.2.尺规作图的基本步骤包括:已知,求作,分析作法,证明,得出结论.步骤顺序不作要求,但作图时一定要保留作图痕迹,作图后不要忘记写结论.
尺规作图易漏解[德州中考]在公路l1同侧、l2异侧有两个城镇A,B,如图25-11.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置(保留作图痕迹,不要求写作法).
【错解】由题意可知,点C应满足两个条件:一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是这两条线的交点.(1)作两条公路夹角的平分线OD;(2)作线段AB的垂直平分线FG.则射线OD与直线FG的交点C1就是所求的位置.【错因】忽略了作两条公路另一个夹角的平分线OE,则漏掉了射线OE与直线FG的交点C2.
2024年中考数学复习课件---第25讲 尺规作图: 这是一份2024年中考数学复习课件---第25讲 尺规作图,共25页。PPT课件主要包含了栏目导航,尺规作图,五种基本尺规作图,如图点D即为所求,如图DM即为所求等内容,欢迎下载使用。
中考数学复习第七章尺规作图及图形变换第25课时投影与视图课件: 这是一份中考数学复习第七章尺规作图及图形变换第25课时投影与视图课件,共41页。PPT课件主要包含了课前循环练,新课标,考点梳理,广东中考,高分击破,中考演练,命题趋势,限时5分钟,08a,一个点等内容,欢迎下载使用。
中考数学复习第七章尺规作图及图形变换第25课时投影与视图课件: 这是一份中考数学复习第七章尺规作图及图形变换第25课时投影与视图课件,共20页。












