第七单元 第21课时 三角形的基础知识（含答案）

这是一份第七单元 第21课时 三角形的基础知识（含答案），共29页。PPT课件主要包含了小题热身，图21－1，图21－2，图21－3，考点管理，不在同一条，图21－4，图21－5，变式跟进答图，图21－6等内容，欢迎下载使用。

1．下列各组数中，不可能成为一个三角形三边长的是 (　 　)A．2，3，4 B．5，7，7C．5，6，12 D．6，8，10【解析】 判断三条线段a，b，c能否组成三角形的常用方法：当两条较短线段之和大于最长线段时，则能组成三角形．∵2＋3>4，5＋7>7，5＋6<12，6＋8>10，∴5，6，12不可能成为一个三角形的三边长．
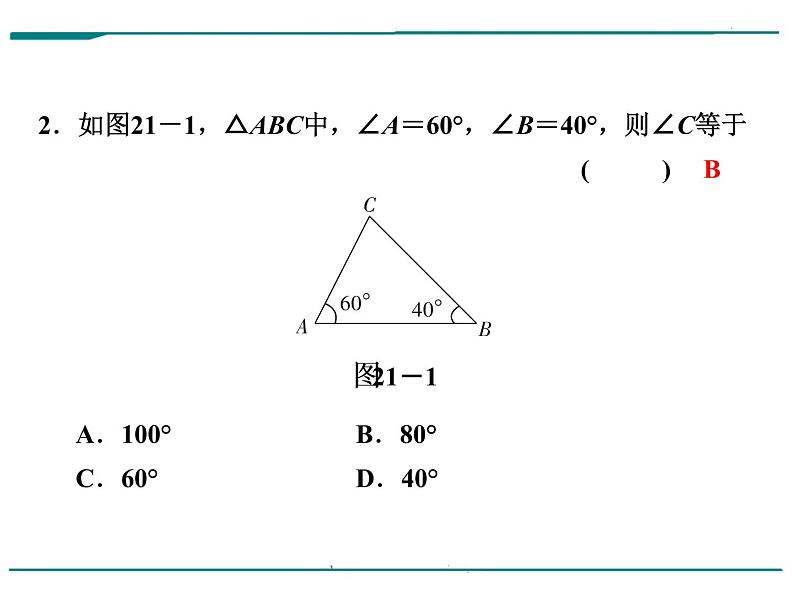
2．如图21－1，△ABC中，∠A＝60°，∠B＝40°，则∠C等于 (　 　)    A．100° B．80°C．60° D．40°
3．如图21－2，在△ABC中，∠BAC＝x°，∠B＝2x°，∠C＝3x°，则∠BAD的度数是 (　 　) A．145° B．150°C．155° D．160°【解析】 在△ABC中，∵∠B＋∠C＋∠BAC＝180°，∠BAC＝x°，∠B＝2x°，∠C＝3x°，∴6x°＝180°，∴x＝30，∴∠BAD＝∠B＋∠C＝5x°＝150°.
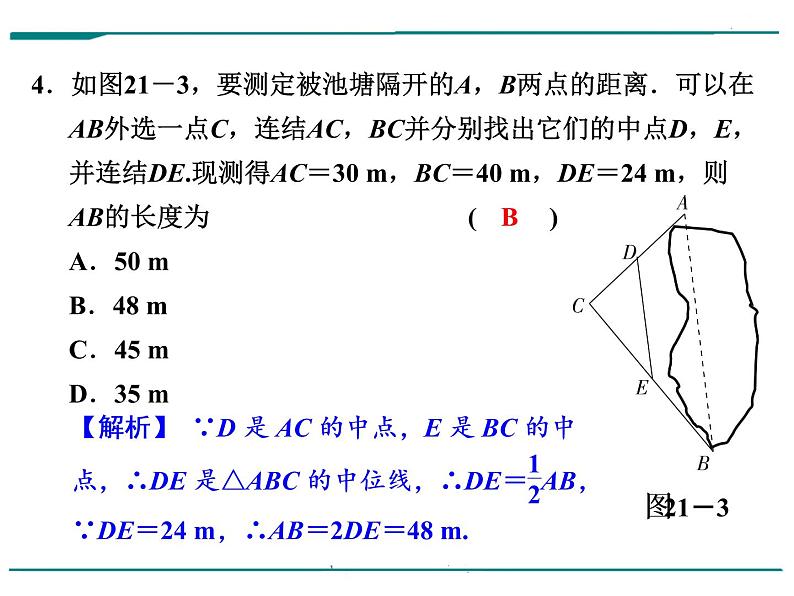
4．如图21－3，要测定被池塘隔开的A，B两点的距离．可以在AB外选一点C，连结AC，BC并分别找出它们的中点D，E，并连结DE.现测得AC＝30 m，BC＝40 m，DE＝24 m，则AB的长度为 (　 　)A．50 mB．48 mC．45 mD．35 m
一、必知4 知识点1．三角形的概念及分类定义：由_______________直线上的三条线段首尾顺次相接所组成的图形是三角形．三角形的分类：(1)按角分：
【智慧锦囊】(1)三角形的三条中线的交点在三角形的内部；(2)三角形的三条角平分线的交点在三角形的内部；(3)锐角三角形的三条高线的交点在三角形的内部；直角三角形的三条高线的交点是直角顶点；钝角三角形的三条高线所在直线的交点在三角形的外部．
2．三角形三边的关系(1)三角形任意两边的和________第三边；(2)三角形任意两边的差________第三边．3．三角形内角和定理：三角形的内角和等于_________．推论：(1)三角形的外角________与它不相邻的两个内角的和；(2)三角形的一个外角________任意一个和它不相邻的内角．
【智慧锦囊】一个三角形中，最多有三个锐角，最少有两个锐角，最多有一个钝角，最多有一个直角．
4．三角形的中位线三角形的中位线________于第三边，并且等于第三边的一半．5．三角形的重心(选学内容)三角形的重心：三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．
二、必会2 方法1．三角形内外角性质的运用技巧进行三角形角度计算时，常常利用方程求解．2．构造三角形中位线有关中点问题，常作辅助线构造三角形中位线，利用三角形中位线的性质解决问题．
三角形的三边关系　[2017·舟山]长度分别为2，7，x的三条线段能组成一个三角形，x的值可以是(　 　)A．4 B．5 C．6 D．9【解析】 利用“三角形的任意两边之和大于第三边，三角形的任意两边之差小于第三边”可得7－2＜x＜7＋2，解得5＜x＜9，x的值可以是6.
1．现有长分别为3 cm，4 cm，7 cm，9 cm的四根木棒，任取其中三根组成一个三角形，那么可以组成的三角形的个数是 (　 　)A．1 B．2 C．3 D．4【解析】 四根木棒中任取三根的所有组合：3，4，7；3，4，9；3，7，9；4，7，9，只有3，7，9和4，7，9能组成三角形．故选B.
【点悟】　三角形两边之和大于第三边，两边之差小于第三边是判断任意三条线段能否组成三角形的依据．
三角形的角平分线性质的运用 　如图21－4，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，∠BAC ＝ 60°，∠ABE＝25°，则∠DAC的大小是 (　 　)A．15° B．20°C．25° D．30°【解析】 由角平分线和三角形内角和的知识可以知道，∠ABC＝50°，∠BAC＝60°，∠C＝70°，则∠DAC＝20°.
如图21－5，在△ABC中，AB＝AC，∠A＝30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D等于 (　 　)A．15° B．17.5°C．20° D．22.5°　　
三角形的中位线的性质运用　如图21－6，在△ABC中，∠ACB＝90°，点D，E，F分别是AB，BC，CA的中点，若CD＝2，则线段EF的长是_____．
1．[2017·淮安]如图21－7，在Rt△ABC中，∠ACB＝90°，D，E分别是AB，AC的中点，F是AD的中点．若AB＝8，则EF＝_____．
2．如图21－8，在△ABC中，AB＝5，AC＝3，AD，AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB于点F，连结DH，则线段DH的长为_____．
【点悟】　三角形的中位线定理在证明两线平行关系和计算两线段数量关系时有着重要作用，因此，题目中有“中点”，要学会寻找或构造中位线，从而为解题创造条件．
三角形的重心(选学内容) 　如图21－9，已知在Rt△ABC中，∠C＝90°，AC＝BC，AB＝6，点P是Rt△ABC的重心，则点P到AB所在直线的距离等于 (　 　)
【点悟】　三角形的顶点、重心、对边中点共线，所以有关重心的辅助线是连结三角形的顶点与重心得到三角形的中线．
2．在△ABC中，已知BD和CE分别是边AC，AB上的中线，且BD⊥CE，垂足为O.若OD＝2 cm，OE＝4 cm，则线段AO的长度为_______cm.
必明3 易错点1．判断三条线段能否构成三角形时，要注意不能只考虑两边之和大于第三边就下结论，应该依据较小两边的和大于最大边来判断．2．三角形的中位线与中线的区别：三角形的中线是连结顶点与对边中点的线段，而中位线是连结三角形两边中点的线段．3．不同类型的三角形的三条高线所在的位置各不相同，因此在解涉及三角形的高线的问题时，常常需要分类讨论高线在“形内”“形上”还是“形外”．