






还剩23页未读,
继续阅读
高中物理人教版 (新课标)选修3选修3-3第八章 气体1 气体的等温变化图片课件ppt
展开
这是一份高中物理人教版 (新课标)选修3选修3-3第八章 气体1 气体的等温变化图片课件ppt,共31页。PPT课件主要包含了p1V1=p2V2,双曲线,等温线,气体压强的求法,答案BD,压强的计算,玻意耳定律的基本应用等内容,欢迎下载使用。
第1讲 气体的等温变化
目标定位 1.知道玻意耳定律的内容、表达式及适用条件.2.能运用玻意耳定律对有关问题进行分析、计算.3.了解p-V图、p- 图的物理意义.
预习导学 梳理·识记·点拨
1.气体的状态参量生活中的许多现象都表明,气体的 、 、 三个状态参量之间存在着一定的关系.2.玻意耳定律(1)内容:一定质量的某种气体,在 不变的情况下,压强与体积成 .(2)公式:pV=C或.
(3)条件:气体的 一定, 不变.(4)气体等温变化的p-V图象:气体的压强p随体积V的变化关系如图1所示,图线的形状为 ,它描述的是温度不变时的p-V关系,称为 .一定质量的气体,不同温度下的等温线是不同的.
想一想 如图1所示,为同一气体在不同温度下的等温线,T1和T2哪一个大?答案 T1大于T2.因为体积相同时,温度越高,压强越大.
课堂讲义 理解·深化·探究
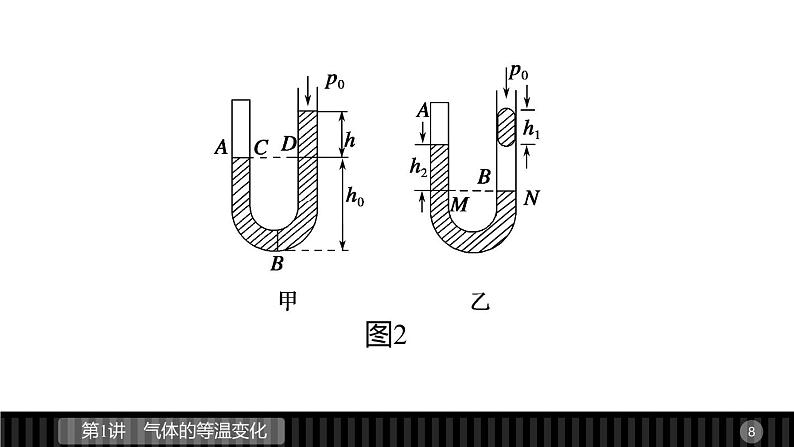
1.液柱封闭气体取等压面法:同种液体在同一深度液体的压强相等,在连通器中,灵活选取等压面,利用两侧压强相等求解气体压强.如图2甲所示,同一液面C、D两处压强相等,故pA=p0+ph;如图乙所示,M、N两处压强相等.故有pA+ph2=pB,从右侧管看,有pB=p0+ph1.
2.活塞封闭气体选与封闭气体接触的液柱或活塞为研究对象,进行受力分析,再利用平衡条件求压强.如图3甲所示,汽缸截面积为S,活塞质量为M.在活塞上放置质量为m的铁块,设大气压强为p0,试求封闭气体的压强.
以活塞为研究对象,受力分析如图乙所示.由平衡条件得:Mg+mg+p0S=pS,即:p=p0+ .
例1 如图4所示,竖直放置的U形管,左端开口,右端封闭,管内有a、b两段水银柱,将A、B两段空气柱封闭在管内.已知水银柱a长h1为10 cm,水银柱b两个液面间的高度差h2为5 cm,大气压强为75 cmHg,求空气柱A、B的压强分别是多少?
解析 设管的截面积为S,选a的下端面为参考液面,它受向下的压力为(pA+ph1)S,受向上的大气压力为p0S,由于系统处于静止状态,则(pA+ph1)S=p0S,所以pA=p0-ph1=(75-10)cmHg=65 cmHg,再选b的左下端面为参考液面,由连通器原理知:液柱h2的上表面处的压强等于pB,则(pB+ph2)S=pAS,所以pB=pA-ph2=(65-5)cmHg=60 cmHg.答案 65 cmHg 60 cmHg
借题发挥 (1)在考虑与气体接触的液柱所产生的附加压强p=ρgh时,应特别注意h是表示液面竖直高度,不一定是液柱长度.(2)特别注意大气压强的作用,不要漏掉大气压强.
二、玻意耳定律的理解及应用
1.成立条件:(1)质量一定,温度不变.(2)温度不太低,压强不太大.
3.应用玻意耳定律解题的一般步骤(1)确定研究对象,并判断是否满足玻意耳定律的条件.
(2)确定初、末状态及状态参量(p1、V2;p2、V2).(3)根据玻意耳定律列方程求解.(注意统一单位)(4)注意分析隐含条件,作出必要的判断和说明.
例2 如图5所示,活塞的质量为m,缸套的质量为M,通过弹簧吊在天花板上,汽缸内封住一定质量的气体,缸套和活塞间无摩擦,活塞面积为S,大气压强为p0,则封闭气体的压强为( )
解析 以缸套为研究对象,有pS+Mg=p0S,所以封闭气体的压强p=p0- ,故应选C.对于活塞封闭气体类问题压强的求法,灵活选取研究对象会使问题简化.答案 C
例3 粗细均匀的玻璃管,一端封闭,长为12 cm.一个人手持玻璃管开口竖直向下潜入水中,当潜到水下某深度时看到水进入玻璃管口2 cm,求管口距液面的深度.(取水面上大气压强为p0=1.0×105 Pa,g取10 m/s2,池水中温度恒定)
解析 确定研究对象为被封闭的一部分气体,玻璃管下潜的过程中气体的状态变化可视为等温过程.设潜入水下的深度为h,玻璃管的横截面积为S.气体的初、末状态参量分别为:
初状态:p1=p0,V1=12S末状态:p2=p0+ρg(h-0.02),V2=10S由玻意耳定律p1V1=p2V2,得p0·12S=[p0+ρg(h-0.02)]·10S解得:h=2.02 m.答案 2.02 m
三、等温变化中p-V图象和p- 图象的理解和应用
1.一定质量的气体,在p V图象中等温线是双曲线,双曲线上的每一个点,均表示一定质量的气体在该温度下的一个状态,而且同一条等温线上每个点对应的p、V坐标的乘积都是相等的.一定质量的气体在不同温度下的等温线是不同的双曲线,且pV乘积越大,温度越高,如图6所示:T2>T1.
2.一定质量气体的等温变化过程,也可以用p- 图象表示,如图7所示.等温线是通过原点的直线,由于气体的体积不能无穷大,所以靠近原点附近处应用虚线表示,该直线的斜率k= =pV∝T,即斜率越大,气体做等温变化的温度越高.
例4 如图8所示,为一定质量的气体在不同温度下的两条p- 图线,由图可知( )A.一定质量的气体在发生等温变化时,其压 强与体积成正比B.一定质量的气体在发生等温变化时,其 p- 图线的延长线是经过坐标原点的C.T1>T2D.T1
对点练习 巩固·应用·反馈
1.求图9中被封闭气体A的压强.其中(1)、(2)、(3)图中的玻璃管内都装有水银,(4)图中的小玻璃管浸没在水中.大气压强p0=76 cmHg.(p0=1.01×105 Pa,g=10 m/s2,ρ水=1×103 kg/m3)
解析 (1)pA=p0-ph=76 cmHg-10 cmHg=66 cmHg.(2)pA=p0-ph=76 cmHg-10×sin 30° cmHg=71 cmHg.(3)pB=p0+ph2=76 cmHg+10 cmHg=86 cmHgpA=pB-ph1=86 cmHg-5 cmHg=81 cmHg.(4)pA=p0+ρ水gh=1.01×105 Pa+1×103×10×1.2 Pa=1.13×105 Pa.
答案 (1)66 cmHg(2)71 cmHg(3)81 cmHg(4)1.13×105 Pa
2.一个气泡由湖面下20 m深处缓慢上升到湖面下10 m深处,它的体积约变为原来体积的( )A.3倍 B.2倍C.1.5倍 D.0.7倍
解析 气泡缓慢上升过程中,温度不变,气体等温变化,湖面下20 m处,水的压强约为2个标准大气压(1个标准大气压相当于10 m水产生的压强),故p1=3 atm,p2=2 atm,由p1V1=p2V2,得: =1.5,故C项正确.
3.一定质量的气体,压强为3 atm,保持温度不变,当压强减小了2 atm,体积变化了4 L,则该气体原来的体积为( )
解析 设原来的体积为V,则3V=(3-2)(V+4),得V=2 L.
p-V图象或p- 图象
4.下图中,p表示压强,V表示体积,T为热力学温度,各图中正确描述一定质量的气体发生等温变化的是( )
第1讲 气体的等温变化
目标定位 1.知道玻意耳定律的内容、表达式及适用条件.2.能运用玻意耳定律对有关问题进行分析、计算.3.了解p-V图、p- 图的物理意义.
预习导学 梳理·识记·点拨
1.气体的状态参量生活中的许多现象都表明,气体的 、 、 三个状态参量之间存在着一定的关系.2.玻意耳定律(1)内容:一定质量的某种气体,在 不变的情况下,压强与体积成 .(2)公式:pV=C或.
(3)条件:气体的 一定, 不变.(4)气体等温变化的p-V图象:气体的压强p随体积V的变化关系如图1所示,图线的形状为 ,它描述的是温度不变时的p-V关系,称为 .一定质量的气体,不同温度下的等温线是不同的.
想一想 如图1所示,为同一气体在不同温度下的等温线,T1和T2哪一个大?答案 T1大于T2.因为体积相同时,温度越高,压强越大.
课堂讲义 理解·深化·探究
1.液柱封闭气体取等压面法:同种液体在同一深度液体的压强相等,在连通器中,灵活选取等压面,利用两侧压强相等求解气体压强.如图2甲所示,同一液面C、D两处压强相等,故pA=p0+ph;如图乙所示,M、N两处压强相等.故有pA+ph2=pB,从右侧管看,有pB=p0+ph1.
2.活塞封闭气体选与封闭气体接触的液柱或活塞为研究对象,进行受力分析,再利用平衡条件求压强.如图3甲所示,汽缸截面积为S,活塞质量为M.在活塞上放置质量为m的铁块,设大气压强为p0,试求封闭气体的压强.
以活塞为研究对象,受力分析如图乙所示.由平衡条件得:Mg+mg+p0S=pS,即:p=p0+ .
例1 如图4所示,竖直放置的U形管,左端开口,右端封闭,管内有a、b两段水银柱,将A、B两段空气柱封闭在管内.已知水银柱a长h1为10 cm,水银柱b两个液面间的高度差h2为5 cm,大气压强为75 cmHg,求空气柱A、B的压强分别是多少?
解析 设管的截面积为S,选a的下端面为参考液面,它受向下的压力为(pA+ph1)S,受向上的大气压力为p0S,由于系统处于静止状态,则(pA+ph1)S=p0S,所以pA=p0-ph1=(75-10)cmHg=65 cmHg,再选b的左下端面为参考液面,由连通器原理知:液柱h2的上表面处的压强等于pB,则(pB+ph2)S=pAS,所以pB=pA-ph2=(65-5)cmHg=60 cmHg.答案 65 cmHg 60 cmHg
借题发挥 (1)在考虑与气体接触的液柱所产生的附加压强p=ρgh时,应特别注意h是表示液面竖直高度,不一定是液柱长度.(2)特别注意大气压强的作用,不要漏掉大气压强.
二、玻意耳定律的理解及应用
1.成立条件:(1)质量一定,温度不变.(2)温度不太低,压强不太大.
3.应用玻意耳定律解题的一般步骤(1)确定研究对象,并判断是否满足玻意耳定律的条件.
(2)确定初、末状态及状态参量(p1、V2;p2、V2).(3)根据玻意耳定律列方程求解.(注意统一单位)(4)注意分析隐含条件,作出必要的判断和说明.
例2 如图5所示,活塞的质量为m,缸套的质量为M,通过弹簧吊在天花板上,汽缸内封住一定质量的气体,缸套和活塞间无摩擦,活塞面积为S,大气压强为p0,则封闭气体的压强为( )
解析 以缸套为研究对象,有pS+Mg=p0S,所以封闭气体的压强p=p0- ,故应选C.对于活塞封闭气体类问题压强的求法,灵活选取研究对象会使问题简化.答案 C
例3 粗细均匀的玻璃管,一端封闭,长为12 cm.一个人手持玻璃管开口竖直向下潜入水中,当潜到水下某深度时看到水进入玻璃管口2 cm,求管口距液面的深度.(取水面上大气压强为p0=1.0×105 Pa,g取10 m/s2,池水中温度恒定)
解析 确定研究对象为被封闭的一部分气体,玻璃管下潜的过程中气体的状态变化可视为等温过程.设潜入水下的深度为h,玻璃管的横截面积为S.气体的初、末状态参量分别为:
初状态:p1=p0,V1=12S末状态:p2=p0+ρg(h-0.02),V2=10S由玻意耳定律p1V1=p2V2,得p0·12S=[p0+ρg(h-0.02)]·10S解得:h=2.02 m.答案 2.02 m
三、等温变化中p-V图象和p- 图象的理解和应用
1.一定质量的气体,在p V图象中等温线是双曲线,双曲线上的每一个点,均表示一定质量的气体在该温度下的一个状态,而且同一条等温线上每个点对应的p、V坐标的乘积都是相等的.一定质量的气体在不同温度下的等温线是不同的双曲线,且pV乘积越大,温度越高,如图6所示:T2>T1.
2.一定质量气体的等温变化过程,也可以用p- 图象表示,如图7所示.等温线是通过原点的直线,由于气体的体积不能无穷大,所以靠近原点附近处应用虚线表示,该直线的斜率k= =pV∝T,即斜率越大,气体做等温变化的温度越高.
例4 如图8所示,为一定质量的气体在不同温度下的两条p- 图线,由图可知( )A.一定质量的气体在发生等温变化时,其压 强与体积成正比B.一定质量的气体在发生等温变化时,其 p- 图线的延长线是经过坐标原点的C.T1>T2D.T1
对点练习 巩固·应用·反馈
1.求图9中被封闭气体A的压强.其中(1)、(2)、(3)图中的玻璃管内都装有水银,(4)图中的小玻璃管浸没在水中.大气压强p0=76 cmHg.(p0=1.01×105 Pa,g=10 m/s2,ρ水=1×103 kg/m3)
解析 (1)pA=p0-ph=76 cmHg-10 cmHg=66 cmHg.(2)pA=p0-ph=76 cmHg-10×sin 30° cmHg=71 cmHg.(3)pB=p0+ph2=76 cmHg+10 cmHg=86 cmHgpA=pB-ph1=86 cmHg-5 cmHg=81 cmHg.(4)pA=p0+ρ水gh=1.01×105 Pa+1×103×10×1.2 Pa=1.13×105 Pa.
答案 (1)66 cmHg(2)71 cmHg(3)81 cmHg(4)1.13×105 Pa
2.一个气泡由湖面下20 m深处缓慢上升到湖面下10 m深处,它的体积约变为原来体积的( )A.3倍 B.2倍C.1.5倍 D.0.7倍
解析 气泡缓慢上升过程中,温度不变,气体等温变化,湖面下20 m处,水的压强约为2个标准大气压(1个标准大气压相当于10 m水产生的压强),故p1=3 atm,p2=2 atm,由p1V1=p2V2,得: =1.5,故C项正确.
3.一定质量的气体,压强为3 atm,保持温度不变,当压强减小了2 atm,体积变化了4 L,则该气体原来的体积为( )
解析 设原来的体积为V,则3V=(3-2)(V+4),得V=2 L.
p-V图象或p- 图象
4.下图中,p表示压强,V表示体积,T为热力学温度,各图中正确描述一定质量的气体发生等温变化的是( )
相关课件
选修31 气体的等温变化课文ppt课件: 这是一份选修31 气体的等温变化课文ppt课件
人教版 (新课标)选修31 气体的等温变化说课课件ppt: 这是一份人教版 (新课标)选修31 气体的等温变化说课课件ppt
人教版 (新课标)选修31 气体的等温变化示范课课件ppt: 这是一份人教版 (新课标)选修31 气体的等温变化示范课课件ppt













