专题10 立体几何与空间向量-2021年高考冲刺之二轮专题精讲精析

专题10立体几何与空间向量

一、单选题

1．如图为某几何体的三视图，则该几何体的表面积为（    ）

A． B． C． D．

2．在我国古代数学名著《九章算术》中，将四个面都是直角三角形的四面体称为“鳖臑”，在鳖臑中，平面，，且，为的中点，则异面直线与所成的角为（    ）

A．30° B．45°

C．60° D．90°

3．已知直角三角形的两直角边分别为1，，若绕三角形的斜边旋转一周形成的几何体，则该几何体的体积为（    ）

A． B．

C． D．

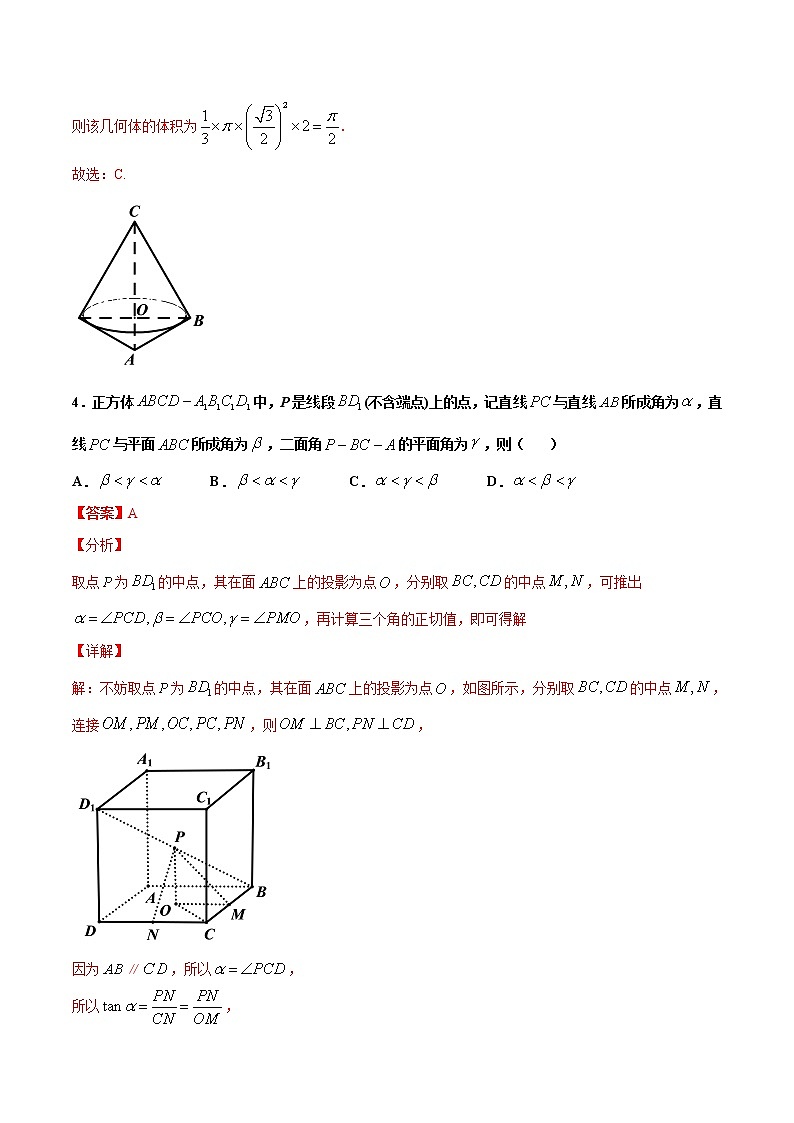
4．正方体中，P是线段(不含端点)上的点，记直线与直线所成角为，直线与平面所成角为，二面角的平面角为，则（    ）

A． B． C． D．

5．如图所示，是二面角棱上的一点，分别在平面内引射线，，如果，设二面角的大小为，则（    ）

A．1 B．

C． D．

6．已知，，若，则的值为（    ）

A． B． C．6 D．8

7．把一个半径为20的半圆卷成圆锥的侧面，则这个圆锥的高为（    ）

A．10 B． C． D．

8．已知，，、分别是平面，的法向量，则平面，的位置关系是（    ）

A．平行

B．垂直

C．所成的二面角为锐角

D．所成的二面角为钝角

9．下列命题正确的是（    ）

A．空间任意三点确定一个平面

B．两条垂直直线确定一个平面

C．一条直线和一点确定一个平面

D．两条平行线确定一个平面

10．已知，是两条不同的直线，，是两个不同的平面，则下列结论一定正确的是（    ）

A．若，，则

B．若，，则

C．若，，，则

D．若，，，则

11．如图，棱长为4的正四面体，，分别是，上的动点，且，则中点的轨迹长度为（    ）

A． B． C． D．

12．已知四面体ABCD的四个面都为直角三角形，平面BCD，，若该四面体的四个顶点都在球O的表面上，则球O的表面积为（    ）

A． B． C． D．

二、填空题

13．已知一个棱长为6cm的正方体塑料盒子（无上盖），上口放着一个半径为5cm的钢球，则球心到盒底的距离为______cm．

14．如图，在四棱锥中，侧面为正三角形，底面为正方形，侧面底面，为底面内的一个动点，且满足，则点在正方形内的轨迹为______．（填序号）

15．已知正四棱锥的所有棱长都相等，是的中点，则，所成角的正弦值为______．

16．已知下列命题：

：若直线与平面有两个公共点，则直线在平面内.

：若三条直线，，互相平行且分别交直线于，，三点，则这四条直线共面.

：若直线与平面相交，则与平面内的任意直线都是异面直线.

：如果两条异面直线中的一条与一个平面平行，则另一条直线一定与该平面相交.

则下述命题中所有真命题的序号是____________．

①    ②    ③    ④

三、解答题

17．如图甲，已知直角梯形ABCD，AB//CD，AB＝2CD＝2BC＝4，，E为AB的中点，将三角形ADE沿DE折起，使点A到达点F（如图乙），且.

（1）证明：DE⊥平面FEB；

（2）求平面FDE与平面FBC所成的锐二面角的余弦值.

18．如图甲，设长方形的边，，点、分别满足，，如图乙，将直角梯形沿直线折到的位置.

（1）证明：平面；

（2）当二面角为直二面角时，求多面体的体积；

（3）若中点的，当在底面上的射影恰好落在上，且时，求二面角所成角的余弦值.（如图丙）

19．如图，在四棱锥中，底面为菱形，，侧面是边长为2的正三角形，为的中点，且平面．

（1）证明：平面平面；

（2）求三棱锥的高.

20．如图，正方体中，、分别为、的中点．选用合适的方法证明以下问题：

（1）证明：平面平面；

（2）证明：面．

21．已知长方体中，，，E，F分别是，的中点.

（1）求证：直线平面；

（2）求直线与平面所成角的正弦值.

22．在四棱锥中，平面平面，底面为直角梯形，，，，为线段的中点，过的平面与线段，分别交于点，．

（1）求证：平面；

（2）若，点为的中点，求直线与平面所成角的正弦值.