（人教版）数学中考总复习45中考总复习：图形的变换（基础）珍藏版

中考总复习：图形的变换--巩固练习（基础）

【巩固练习】

一、选择题

1. 以下图形：平行四边形、矩形、等腰三角形、线段、圆、菱形，其中既是轴对称图形又是中心对称图形的有（    ）.

   A．4个     B．5个     C．6个    D．3个

2．有以下现象：①温度计中，液柱的上升或下降；②打气筒打气时，活塞的运动；③钟摆的摆动；④传送带上瓶装饮料的移动，其中属于平移的是（    ）.

   A．①③     B．①②    C．②③    D．②④

3.在图形的平移中，下列说法中错误的是（    ）.

    A．图形上任意点移动的方向相同；     B．图形上任意点移动的距离相同

    C．图形上可能存在不动点；           D．图形上任意对应点的连线长相等

4.如图，O是正六边形ABCDEF的中心，下列图形可由△OBC平移得到的是（    ）.
　　A.△OCD　　　B.△OAB　　　C.△OAF　　　D.△OEF

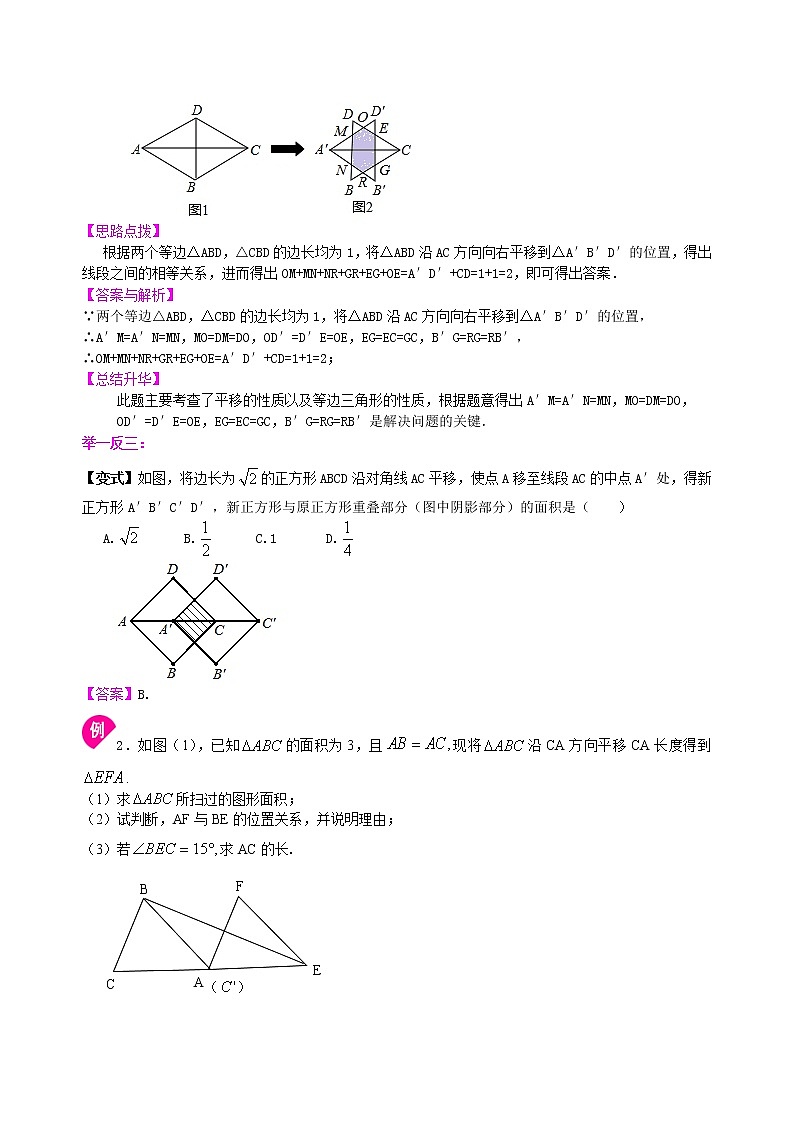
5.如图，将边长为的正方形ABCD沿对角线AC平移，使点A移至线段AC的中点A′处，得新正方形A′B′C′D′，新正方形与原正方形重叠部分(图中阴影部分)的面积是(    ).

A．        B．       C．1        D．

第4题                    第5题                   第6题

6.如图所示，△ABC中，AC＝5，中线AD＝7，△EDC是由△ADB旋转180°所得，则AB边的取值范围是（    ）．

　　A．l＜AB＜29 　　　B．4＜AB＜24　　　 C．5＜AB＜19 　　　D．9＜AB＜19

二、填空题

7. 如图，在边长为2的菱形ABCD中，∠B＝45°，AE为BC边上的高，将△ABE沿AE所在直线翻折后得△AGE，那么△AGE与四边形AECD重叠部分的面积是           ．

第7题                                 第8题

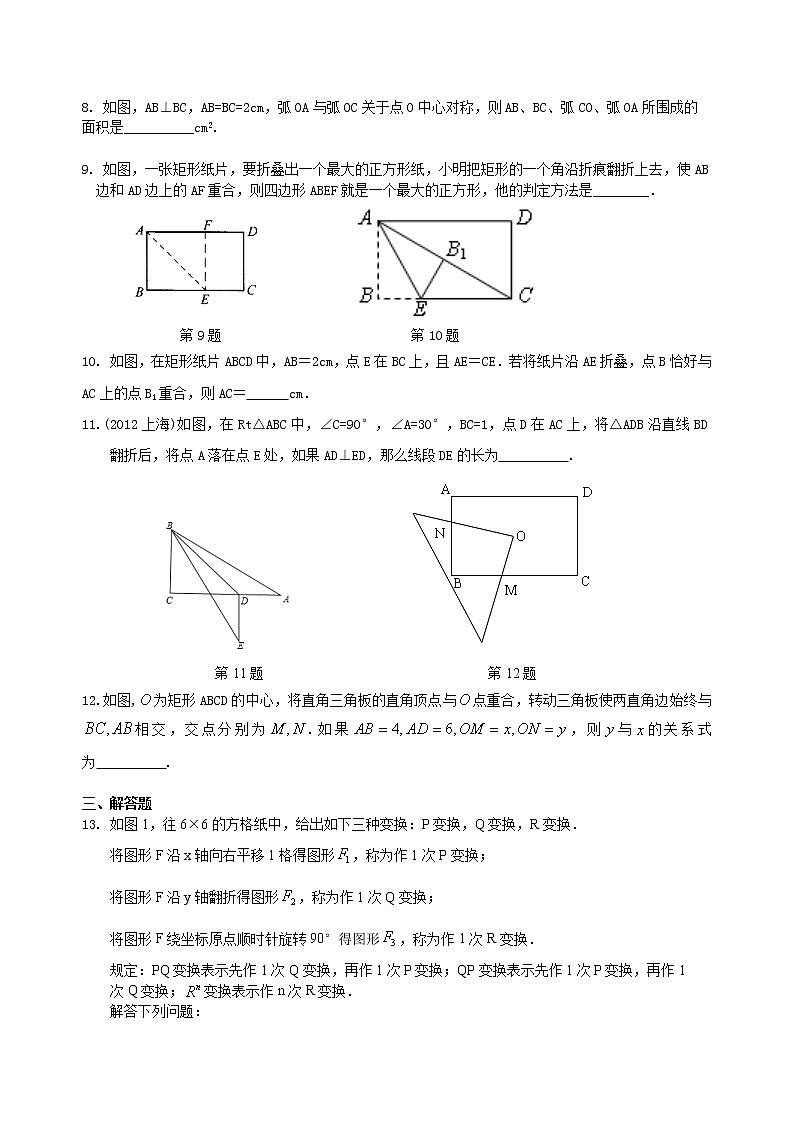
8. 如图，AB⊥BC，AB=BC=2cm，弧OA与弧OC关于点O中心对称，则AB、BC、弧CO、弧OA所围成的面积是__________cm2.
  

9. 如图，一张矩形纸片，要折叠出一个最大的正方形纸，小明把矩形的一个角沿折痕翻折上去，使AB边和AD边上的AF重合，则四边形ABEF就是一个最大的正方形，他的判定方法是________．

第9题                           第10题

10. 如图，在矩形纸片ABCD中，AB＝2cm，点E在BC上，且AE＝CE．若将纸片沿AE折叠，点B恰好与

AC上的点B1重合，则AC＝      cm．

11.(2012上海)如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=1，点D在AC上，将△ADB沿直线BD翻折后，将点A落在点E处，如果AD⊥ED，那么线段DE的长为          .

第11题                                第12题

12.如图,为矩形ABCD的中心，将直角三角板的直角顶点与点重合，转动三角板使两直角边始终与相交，交点分别为.如果，则与的关系式为          .

三、解答题

13. 如图1，往6×6的方格纸中，给出如下三种变换：P变换，Q变换，R变换．
　　将图形F沿x轴向右平移1格得图形，称为作1次P变换；
　　将图形F沿y轴翻折得图形，称为作1次Q变换；
　　将图形F绕坐标原点顺时针旋转90°得图形，称为作1次R变换．
　　规定：PQ变换表示先作1次Q变换，再作1次P变换；QP变换表示先作1次P变换，再作1

次Q变换；变换表示作n次R变换．
　　解答下列问题：
　　(1)作变换相当于至少作________次Q变换；
　　(2)请在图2中画出图形F作变换后得到的图形；
　　(3)PQ变换与QP变换是否是相同的变换？请在图3中画出PQ变换后得到的图形，在图4中

画出QP变换后得到的图形．
　
 

14.把两个全等的等腰直角三角板ABC和EFG（其直角边长均为4）叠放在一起（如图①），且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针方向旋转（旋转角α满足条件：0°＜α＜90°)，四边形CHGK是旋转过程中两三角板的重叠部分（如图②）.

(1)在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论；

(2)连接HK，在上述旋转过程中，设BH=，△GKH的面积为，求与之间的函数关系式，并写出自变量的取值范围；

(3)在(2)的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC面积的？若存在，求出此时的值；若不存在，说明理由.

15.如图，将矩形纸片ABCD按如下顺序进行折叠: 对折、展平, 得折痕EF(如图①); 沿GC折叠, 使点B落在EF上的点B′ 处(如图②)； 展平, 得折痕GC(如图③); 沿GH折叠, 使点C落在DH上的点C′ 处(如图④); 沿GC′ 折叠(如图⑤)； 展平, 得折痕GC′、GH(如图⑥).

(1)求图②中∠BCB′ 的大小；

(2)图⑥中的△GCC′ 是正三角形吗?请说明理由.

16.已知矩形纸片，.将纸片折叠，使顶点A与边CD上的点E重合.

（1）如果折痕FG分别与AD，AB交于点F，G（如图（1）），求DE的长.

（2）如果折痕FG分别与CD，AB交于点F，G（如图（2）），的外接圆与直线BC相切，求折痕FG的长.

【答案与解析】

一．选择题

1．【答案】A．

2．【答案】D.

【解析】①温度计中液柱的上升或下降改变图形的大小，不属于平移；
②打气筒打气时，活塞的运动属于平移；
③钟摆的摆动是旋转，不属于平移；
④传送带上瓶装饮料的移动符合平移的性质，属于平移．

3．【答案】C.

4．【答案】C.

5．【答案】B.

【解析】平移后，正方形A′B′C′D′对角线是正方形ABCD对角线的一半，因为相似形面积比是线段比的平方，所以正方形A′B′C′D′面积是正方形ABCD面积的，而正方形ABCD面积是2，所以正方形A′B′C′D′面积是.

6．【答案】D.

【解析】∵△ADB绕点D旋转180°，得到△EDC，

∴AB=EC,AD=DE，而AD=7，∴AE=14，
在△ACE中，AC=5，
∴AE-AC＜EC＜AC+AE，
即14 -5＜EC＜14+5，∴9＜AD＜19．

二．填空题

7．【答案】2-2．

【解析】在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，故AE=，
由折叠易得△ABG为等腰直角三角形，
∴S△ABG=BA•AG=2，S△ABE=1，∴CG=2BE-BC=2-2，
∴CO=OG=2-，∴S△COG=3-2，
∴重叠部分的面积为2-1-（3-2）=2-2．

8．【答案】2.

【解析】连结AC，如图，
∵AB⊥BC，AB=BC=2cm，
∴△ABC为等腰直角三角形，
又∵弧OA与弧OC关于点O中心对称，
∴OA=OC，弧OA=弧OC，
∴弓形OA的面积=弓形OC的面积，
∴AB、BC、弧CO、弧OA所围成的图形的面积=三角形ABC的面积=×2×2=2（cm2）．

9．【答案】对角线平分内角的矩形是正方形.

10．【答案】4cm.

【解析】∵AB=2cm，AB=AB1∴AB1=2cm，
∵四边形ABCD是矩形，AE=CE，∴∠ABE=∠AB1E=90°
∵AE=CE，∴AB1=B1C，∴AC=4cm．

11.【答案】-1．

【解析】∵在Rt△ABC中，∠C=90°，∠A=30°，BC=1，
∴=，即AC=,
∵将△ADB沿直线BD翻折后，将点A落在点E处，
∴∠ADB=∠EDB，DE=AD，
∵AD⊥ED，∴∠CDE=∠ADE=90°，
∴∠EDB=∠ADB=135°，∴∠CDB=∠EDB-∠CDE=135°-90°=45°，
∵∠C=90°，∴∠CBD=∠CDB=45°，
∴CD=BC=1，∴DE=AD=AC-CD=-1.

12．【答案】.

三.综合题

13．【解析】

(1).2；
　　(2).正确画出图形；
　　(3).变换PQ与变换QP不是相同的变换.正确画出图形，.
　　

14．【解析】

(1).在上述旋转过程中，BH=CK，四边形CHGK的面积不变．
证明：连接CG，KH，
∵△ABC为等腰直角三角形，O（G）为其斜边中点，
∴CG=BG，CG⊥AB，
∴∠ACG=∠B=45°，
∵∠BGH与∠CGK均为旋转角，
∴∠BGH=∠CGK，
在△BGH与△CGK中，
∴△BGH≌△CGK（ASA），
∴BH=CK，S△BGH=S△CGK．
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=S△ABC=××4×4=4，
即：S四边形CHGK的面积为4，是一个定值，在旋转过程中没有变化；
 

（2）∵AC=BC=4，BH=x，
  ∴CH=4-x，CK=x．
  由S△GHK=S四边形CHGK-S△CHK，
   得y=4 -x（4-x），
  ∴y=x2-2x+4．
由0°＜α＜90°，得到BH最大=BC=4，
∴0＜x＜4；
（3）存在．
根据题意，得x2-2x+4=×8，
解这个方程，得x1=1，x2=3，
即：当x=1或x=3时，△GHK的面积均等于△ABC的面积的．

15．【解析】

（1）由折叠的性质知：B′C=BC，
在Rt△B′FC中，
∵cos∠B′CF===，
∴∠B′CF=60°，
即∠BCB′=60°；
（2）根据题意得：GC平分∠BCC′，
∴∠GCB=∠GCC′=∠BCB′=30°，
∴∠GCC′=∠BCD-∠BCG=60°，
由折叠的性质知：GH是线段CC′的对称轴，
∴GC′=GC，
∴△GCC′是正三角形．

16.【解析】在矩形ABCD中，AB=2，AD=1，，∠D=90°．
根据轴对称的性质，得EF=AF=．
∴DF=AD-AF=．在Rt△DEF中，DE=．

（2）设AE与FG的交点为O．根据轴对称的性质，得AO=EO．
取AD的中点M，连接MO．则MO=DE，MO∥DC．
设DE=x，则MO=x，在矩形ABCD中，∠C=∠D=90°，
∴AE为△AED的外接圆的直径，O为圆心．
延长MO交BC于点N，则ON∥CD,
∴∠CNM=180°-∠C=90°,
∴ON⊥BC，四边形MNCD是矩形．
∴MN=CD=AB=2．∴ON=MN-MO=2-x.
∵△AED的外接圆与BC相切，
∴ON是△AED的外接圆的半径,
∴OE=ON=2-x，AE=2ON=4-x．
在Rt△AED中，AD2+DE2=AE2，
∴12+x2=（4-x）2．
解这个方程，得x=． ∴DE=，OE=2-x=．
根据轴对称的性质，得AE⊥FG．
∴∠FOE=∠D=90°

可得,即FO=．
又AB∥CD，∴∠EFO=∠AGO，∠FEO=∠GAO．
  ∴△FEO≌△GAO．∴FO=GO．
∴FG=2FO=．
∴折痕FG的长是．