初中北师大版3 确定二次函数的表达式完美版课件ppt

这是一份初中北师大版3 确定二次函数的表达式完美版课件ppt，共60页。

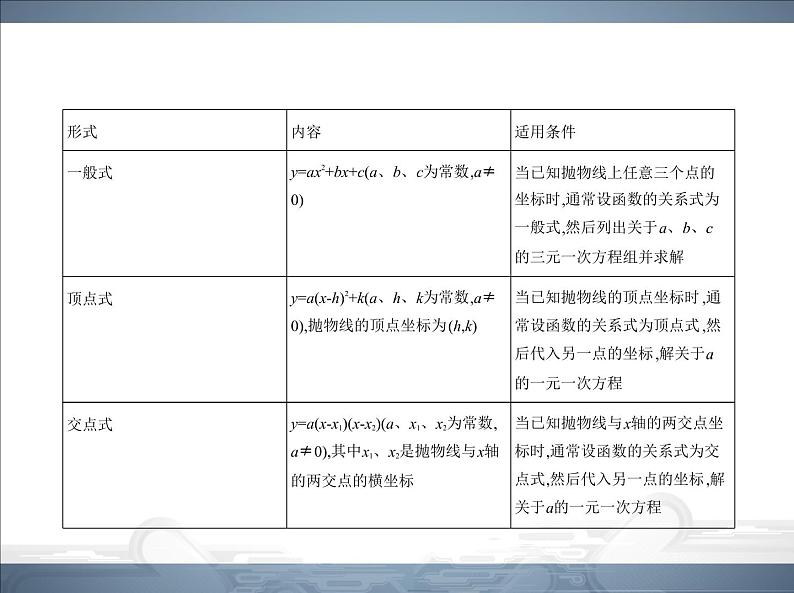
例　分别根据下列条件,求二次函数的表达式.(1)图象经过点(0,0)、(1,1)和(2,5);(2)图象的顶点坐标是(-2,1),且经过点(1,-2);(3)图象与x轴交点的横坐标分别是-2和3,且函数有最小值-3.
分析    (1)已知二次函数图象上的任意三点坐标,可用一般式.(2)已知顶点 坐标,可用顶点式.(3)已知抛物线与x轴的两交点的横坐标,可用交点式.
分析    由图象可知抛物线的对称轴为直线x=1,与x轴的一个交点坐标为(3, 0),由对称性可知与x轴的另一交点坐标为(-1,0),与y轴的交点坐标为(0,3), 利用二次函数的三种表达形式均可求解.
点拨　二次函数有三种不同的表达形式,它们是相互联系的,并可相互转 化.在实际解题时,一定要根据已知条件的特点,灵活选择不同形式的表达 式求解.
知识点    用待定系数法求二次函数的表达式
1.已知x与ax2+bx+c(a≠0)的关系如下表所示,若设y=ax2+bx+c(a≠0),则下列 y与x之间的函数关系式正确的是 (　　)
A.y=x2-4x+3　    B.y=x2-3x+4C.y=x2-3x+3　    D.y=x2-4x+8
答案    A    将三组值分别代入y=ax2+bx+c(a≠0)中,可得a=1,b=-4,c=3,所以y 与x之间的函数关系式为y=x2-4x+3.
5.根据下列条件,分别求出对应的二次函数的解析式.(1)已知抛物线的顶点坐标是(1,2),且过点(2,3);(2)已知二次函数的图象经过(1,-1)、(0,1)、(-1,13)三点;(3)已知抛物线与x轴交于点(1,0)、(3,0),且过点(0,-3).
1.(2018黑龙江大庆龙凤期中)已知一个二次函数,当x=1时,y有最大值8,其 图象的形状、开口方向与抛物线y=-2x2相同,则这个二次函数的表达式是  (　　)A.y=-2x2-x+3　    B.y=-2x2+4C.y=-2x2+4x+8　    D.y=-2x2+4x+6
答案    D    ∵二次函数的图象的形状、开口方向与抛物线y=-2x2相同,∴设 该二次函数的解析式为y=-2(x-h)2+k,∵当x=1时,y有最大值8,∴该二次函数 图象的顶点为(1,8),∴h=1,k=8,∴该二次函数的解析式为y=-2(x-1)2+8,即y=- 2x2+4x+6.
4.已知抛物线y=ax2+bx+c经过点A(5,0)、B(6,-6)和原点,求抛物线的表达式.
解析　因为抛物线经过点A(5,0)和原点,所以设抛物线的表达式为y=ax(x- 5)(a≠0).将B(6,-6)代入y=ax(x-5)(a≠0)中,得-6=6a(6-5),解得a=-1.所以抛物线的表达式为y=-x2+5x.
答案    D　设y与x之间的函数关系式为y=a(x+2)2-2(a≠0),将(0,2)代入y=a(x +2)2-2(a≠0),得2=a(0+2)2-2,解得a=1,故函数关系式为y=(x+2)2-2,故选D.
1.设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上, 且点C到抛物线的对称轴的距离等于1,则抛物线的函数解析式为　　　     　　　　    .
3.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
(1)求该二次函数的关系式;(2)当x为何值时,y有最小值?最小值是多少?(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,试比较y1与y2的大小.
一、填空题1.(2019河北秦皇岛海港模拟,17,★☆☆)把二次函数y=2x2-8x+9化成y=a(x- h)2+k的形式是　　　　　    .
答案    y=2(x-2)2+1
解析    y=2x2-8x+9=2(x2-4x)+9=2(x-2)2+1.
2.(2019北京房山模拟,12,★★☆)写出经过点(0,0),(-2,0)的一个二次函数的 解析式　　　　    (写一个即可).
答案    y=x2+2x(答案不唯一)
解析　∵抛物线过点(0,0),(-2,0),∴设此二次函数的解析式为y=ax(x+2)(a ≠0),把a=1代入,得y=x2+2x.故可填y=x2+2x(答案不唯一).
3.(2019辽宁鞍山台安一模,11,★☆☆)一抛物线和另一抛物线y=-2x2的形状 和开口方向完全相同,且顶点坐标是(-2,1),则该抛物线的解析式为　　     　    .
答案    y=-2(x+2)2+1
解析　设抛物线的解析式为y=a(x-h)2+k(a≠0),∵该抛物线的形状与开口 方向和抛物线y=-2x2相同,∴a=-2,∴y=-2(x-h)2+k,∵顶点坐标是(-2,1),∴y=-2 (x+2)2+1,∴抛物线的解析式为y=-2(x+2)2+1.
4.(2019江苏苏州工业园一模,16,★☆☆)若二次函数y=ax2+bx-3的图象经过 点(-1,0),(3,0),则其表达式为y=　　　    .
答案    x2-2x-3
二、解答题5.(2019上海闵行一模,19,★☆☆)已知在平面直角坐标系xOy中,二次函数y =ax2+bx+c的图象经过点A(1,0)、B(0,-5)、C(2,3),求这个二次函数的解析 式,图象的顶点坐标和对称轴.
6.(2019上海嘉定一模,19,★☆☆)已知抛物线y=x2+bx-3经过点A(1,0),顶点 为点M.(1)求抛物线的表达式及顶点M的坐标;(2)求∠OAM的正弦值.
2.(2019吉林长春一模,18,★★☆)在直角坐标平面内,二次函数图象的顶点 为A(1,-4),且过点B(3,0).(1)求该二次函数的解析式;(2)若点C(-3,12)是抛物线上的另一点,求点C关于对称轴的对称点D的坐标.
4.(2019江苏南京鼓楼二模,24,★★☆)已知二次函数的图象经过点A(-2, 0)、B(1,3)和点C.(1)点C的坐标可以是下列选项中的　　　    ;(只填序号)①(-2,2);②(1,-1);③(2,4);④(3,-4).(2)若点C的坐标为(2,0),求该二次函数的表达式;(3)若点C的坐标为(2,m),二次函数的图象开口向下且对称轴在y轴右侧,结 合函数图象,直接写出m的取值范围.
一、选择题1.(2018山西中考,9,★☆☆)用配方法将二次函数y=x2-8x-9化为y=a(x-h)2+k 的形式为 (　　)A.y=(x-4)2+7　    B.y=(x-4)2-25C.y=(x+4)2+7　    D.y=(x+4)2-25
答案    B    y=x2-8x-9=x2-8x+16-25=(x-4)2-25.
1.(2017山东临沂中考,13,★★☆)足球运动员将足球沿与地面成一定角度 的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地 面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下 表:
下列结论:①足球距离地面的最大高度为20 m;②足球飞行路线的对称轴 是直线t= ;③足球被踢出9 s时落地;④足球被踢出1.5 s时,距离地面的高度是11 m.其中正确结论的个数是 (　　)A.1　    B.2　    C.3　    D.4
答案    B　由题意,设抛物线的解析式为h=at(t-9)(a≠0),把(1,8)代入可得a= -1,∴h=-t2+9t=-(t-4.5)2+20.25,∴足球距离地面的最大高度为20.25 m,抛物线的对称轴为直线t=4.5,故①错误,②正确;∵t=9时,y=0,∴足球被踢出9 s时落地,故③正确;∵t=1.5时,y=11.25,故④错误.∴正确的为②③,故选B.
2.(2017广西百色中考,17,★★☆)经过A(4,0),B(-2,0),C(0,3)三点的抛物线的 解析式是　　　　　　    .
3.(2017上海中考,13,★★☆)已知一个二次函数的图象开口向上,顶点坐标 为(0,-1),那么这个二次函数的解析式可以是　　　    .(只需写一个)
答案    y=x2-1(答案不唯一)
解析　依题意,设二次函数的解析式为y=ax2-1(a≠0),因为抛物线的开口向上,所以a取正数即可.
2.如图,观察小黑点的摆放规律,按照这样的规律继续摆放,记第n个图形中 小黑点的个数为y.解答下列问题:(1)填表:
(2)根据上表中的数据,把n作为横坐标,y作为纵坐标,在平面直角坐标系中 描出相应的各点(n,y),其中1≤n≤5,且n为整数;(3)上述各点会在某一函数的图象上吗?如果在某一函数的图象上,请写出 该函数的表达式.