

初一数学.春季.直升班.教师版.第1讲 实数
展开第一讲
实数
模块一 平方根和立方根
模块二 实数的估算和高斯记号
模块三 实数的概念和分类
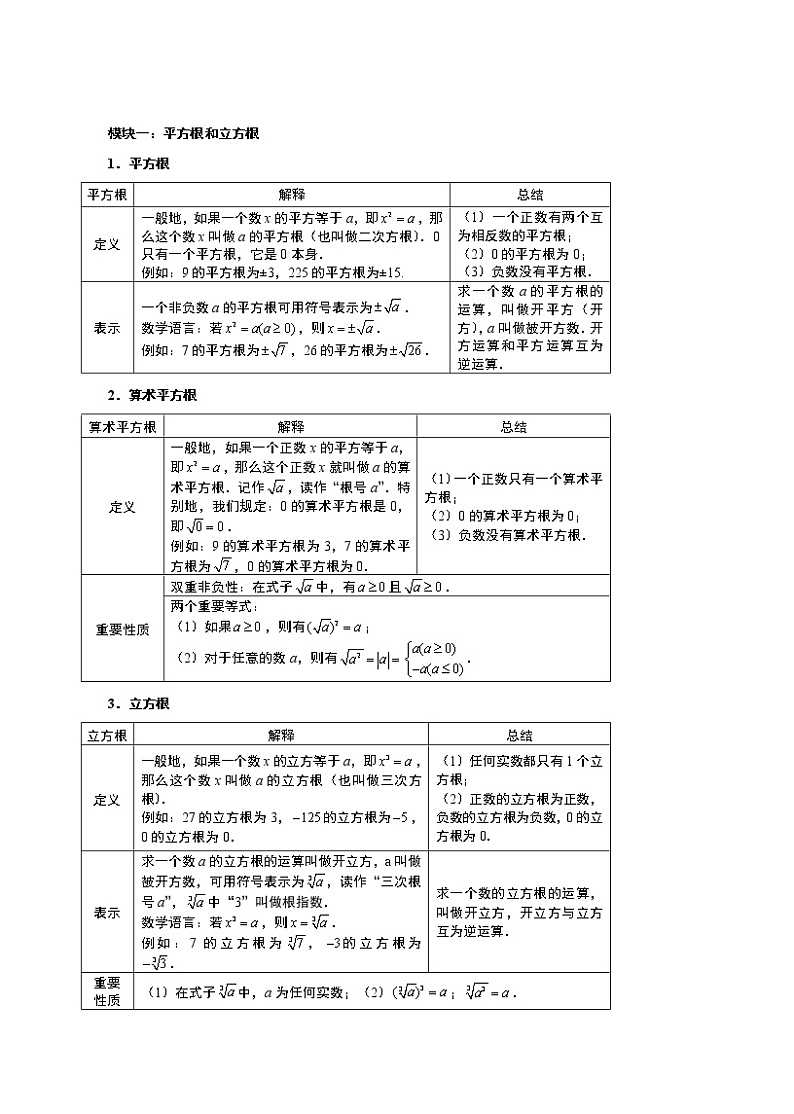
模块一:平方根和立方根
1.平方根
2.算术平方根
3.立方根
模块二:实数的估算和高斯记号
1.估算法:
(1)若,则;
(2)若,则;
根据这两个重要的关系,我们通常可以找距离a最近的两个平方数和立方数,来估算和的大小.例如:,则;,则.
常见实数的估算值:,,.
2.高斯记号:
任何实数都可以由整数部分和小数部分组成,整数部分指的是不超过这个实数的最大整数,小数部分是这个实数减去它的整数部分.
例如:的整数部分为2,那么小数部分为;的整数部分为1,那么小数部分为;的整数部分为,那么小数部分为.
模块三:实数的概念和分类
1.无理数:无限不循环小数叫无理数.
2.实数:有理数和无理数统称实数.
3.实数与数轴的关系:每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上的点是一一对应的.
4.实数的分类
模块一
平方根和立方根
(1)求下列各数的平方根和算术平方根:
①; = 2 \* GB3 ②0.0001; = 3 \* GB3 ③5; = 4 \* GB3 ④; = 5 \* GB3 ⑤.
(2)平方根等于本身的数是________,算术平方根等于它本身的数是________.
(3)一个数的平方根是和,则这个数是________.
(1) = 1 \* GB3 ①和、 = 2 \* GB3 ②和0.01、 = 3 \* GB3 ③和、 = 4 \* GB3 ④和3、 = 5 \* GB3 ⑤和2;
(2)0;0和1;(3)169.
【教师备课提示】这道题主要考查平方根和算术平方根的定义.
判断下列各题,并说明理由
(1)的平方根是.( )
(2)算术平方根一定是正数.( )
(3)一定是正数.( )
(4)没有算术平方根.( )
(5).( )
(6)若,则.( )
(7)是的平方根.( )
(8)的平方根是.( )
(9)的算术平方根是a.( )
(10)若,则.( )
(11)若两个数平方后相等,则这两个数也一定相等.( )
(12)如果两个非负数相等,那么这两个数各自的算术平方根也一定相等.( )
(6)(7)(12)正确.
【教师备课提示】这道题主要考查平方根、算术平方根定义的易错点,这道题建议老师可以以左右手或者开火车的形式讲解,让每个孩子都参与进来.
列举常见易错点:
1.注意区分a的平方根(算术平方根)与的平方根(算术平方根)的计算;如(1).
2.符号问题:0不容忽略,常见错误有:算术平方根一定为正数,非正数一定没有平方根(算术平方根);如(2)(3)(4).
3.逻辑考查;如(7)(8).不能判断符号时需加绝对值;如(9)(10).
(1)已知,求 = 1 \* GB3 ①; = 2 \* GB3 ②.
(2)(七初半期)已知:,则=_______.
(3)已知x、y为实数,,则的平方根为________.
(4)(育才期末)若x、y为实数,且满足,则的算术平方根为________.
(5)(嘉祥2014-2015半期)已知x,y为实数,且那么________.
(1)由题意可得 = 1 \* GB3 ①; = 2 \* GB3 ②;
所以,.由知二推二可以得到:
,
(2)4;(3);(4);(5)—2.
【教师备课提示】这道题主要考查双重非负性,需要分析非负性,并且需要学生注意题目要求的问题,避免粗心,所以做这样的题目一定要看清问题仔细作答.
(1)若,则________;计算的结果是_______.
(2)实数a,b,c在数轴上的位置如图所示:
化简:________.
(3)(育才半期,B26)已知,,求的平方根.
(1)1、1;(2).
(3)由二次根式的定义知:,即,又由二次根式的两个重要等式知:,得:;由非负性知:,则,所以:,平方根:.
【教师备课提示】这道题主要考查二次根式的两个重要等式及对范围的限制,注意,容易出错.
(1)求下列各数的立方根:
= 1 \* GB3 ①; = 2 \* GB3 ②8; = 3 \* GB3 ③; = 4 \* GB3 ④; = 5 \* GB3 ⑤
(2)已知:的平方根为,的立方根为4,求的值.
(3)已知,,且,,求xy的值.
(1) = 1 \* GB3 ①; = 2 \* GB3 ②2; = 3 \* GB3 ③; = 4 \* GB3 ④2; = 5 \* GB3 ⑤;
(2)53;
(3)∵,∴,∵,∴;
又∵,∴,解得,,
进而可得,,.
【教师备课提示】这道题主要考查立方根、平方根的定义和性质(需要更加细心).
计算:(1) (2)
(3) (4)
(1);(2);(3);(4).
【教师备课提示】这道题主要考查平方根和立方根基础的计算.
模块二
实数的估算和高斯记号
(1)若,则估计m的范围为( ).
A. B. C. D.
(2)比较下列各数大小:
= 1 \* GB3 ①; = 2 \* GB3 ②____; = 3 \* GB3 ③_____; = 4 \* GB3 ④____.
(1)B;(2) = 1 \* GB3 ①>; = 2 \* GB3 ②<; = 3 \* GB3 ③>; = 4 \* GB3 ④>.
(1)对于一个无理数m,我们把不超过m的最大整数叫做m的整数部分,把m减去整数部分的差叫做m的小数部分.设,a是x的小数部分,b是的小数部分.求的值.
(2)(成外半期)若与的小数部分分别为a与b,则_______.
(3)设表示不大于x的最大整数,则________.
(1)由的近似值知,
所以x的整数部分为2,,
又,所以的整数部分为,.
于是..
(2)1;
(3)∵
……
.
∴原式.
【教师备课提示】这道题主要考察高斯记号.
模块三
实数的概念和分类
(1),,,,3.14,,,0.61414,……这9个实数中,无理数的个数是( ).
A.1 B.2 C.3 D.4
(2)下面有四个命题:
= 1 \* GB3 ①有理数与无理数之和是无理数;②有理数与无理数之积是无理数;
③无理数与无理数之和是无理数;④无理数与无理数之积是无理数.
请你判断哪些是正确的,哪些是不正确的,并说明理由.
(1)D.,,,…,是无理数.
(可以开火车)
(2)设a,b是有理数,,是无理数.(可以通过举实际例子)
①若,则,此式左边是无理数,右边是有理数,它是不成立的,故是无理数.①正确.
②当时,是有理数,②不正确;
③当,时,是有理数,故③不正确;
④当时,是有理数,故④不正确.
【教师备课提示】这道题主要考查实数的分类和性质考查.
已知x,y是有理数,且,求x,y的值.
已知等式可变形为,
因为x,y是有理数,所以,
化简得,解之得.
【教师备课提示】这道题主要是应用下实数的性质.注意如果说上述式子不为0,而只为有理数,则整理后可以得到一个等量关系.
教师备选
证明是无理数.
用反证法.假设不是无理数,则是有理数,
设(p,q是互质的正整数)
两边同时平方后,整理得,所以p一定是偶数.
设(m是自然数),代入上式得,.
所以q是也是偶数,p与q均为偶数和p,q互质矛盾,
所以不是有理数,于是是无理数.
复习巩固
模块一
平方根和立方根
求下列各式的值:
(1) (2) (3) (4)
(5) (6) (7)
(1)5;(2);(3);(4)2;(5)6;(6);(7)0.1ab.
(1)的平方根是,的算术平方根是,则________.
(2)已知与互为相反数,则的平方根是________.
(3)(青羊区期末,B22)已经,则值是________.
(4)已知x,y为实数,且满足,那么_______.
(1)8;(2),平方根为;(3)3;(4)或0.
(1)立方根等于它本身的数是________;平方根与立方根相等的数是________.
(2)下列说法中,正确的是( ).
A.的算术平方根是0.2 B.的平方根是4
C.的立方根是 D.的立方根为2
(3)(青羊期末)已知,那么的立方根是________.
(4)若,那么的立方根是______.
(1)和;;(2)D;(3);
(4)由二次根式和绝对值的非负性可知,所以:
,故.那么的立方根为2.
计算:(1)
(2)
(3)
(1);(2);(3).
模块二
实数的估算和高斯记号
(1)数轴上在表示数的点A和表示数的点B之间表示整数的点共有______个.
(2)观察例题:∵,即,
∴的整数部分为2,小数部分为.
请你观察上述的规律后试解下面的问题:如果的小数部分为a,的小数部分为b,求的值.
(3)设的整数部分为,小数部分为,则________.
(1)4个;
(2),,原式=;
(3).
模块三
实数的概念和分类
(1)在实数,,,,,,……中,其中无理数的个数为( )
A. B.2 C.3 D.4
(2)已知a、b、c在数轴上的位置如图:化简:____.
(3)(西川半期,B25)已知a,b为有理数,m,n分别表示的整数部分和小数部分,且,求________.
(1)C;(2);
(3)因为:,,,
因此,整数部分,小数部分,
将m,n代入等式,
得:,
又由有理数的封闭性,将式子中的有理项合并,无理项合并,
得:,
因此可得:,即:,因此可得:.平方根
解释
总结
定义
一般地,如果一个数x的平方等于a,即,那么这个数x叫做a的平方根(也叫做二次方根).0只有一个平方根,它是0本身.
例如:9的平方根为±3,225的平方根为±15.
(1)一个正数有两个互为相反数的平方根;
(2)0的平方根为0;
(3)负数没有平方根.
表示
一个非负数a的平方根可用符号表示为.
数学语言:若,则.
例如:7的平方根为,26的平方根为.
求一个数a的平方根的运算,叫做开平方(开方),a叫做被开方数.开方运算和平方运算互为逆运算.
算术平方根
解释
总结
定义
一般地,如果一个正数x的平方等于a,即,那么这个正数x就叫做a的算术平方根.记作,读作“根号a”.特别地,我们规定:0的算术平方根是0,即.
例如:9的算术平方根为3,7的算术平方根为,0的算术平方根为0.
(1)一个正数只有一个算术平方根;
(2)0的算术平方根为0;
(3)负数没有算术平方根.
重要性质
双重非负性:在式子中,有且.
两个重要等式:
(1)如果,则有;
(2)对于任意的数a,则有.
立方根
解释
总结
定义
一般地,如果一个数x的立方等于a,即,那么这个数x叫做a的立方根(也叫做三次方根).
例如:27的立方根为3,的立方根为,0的立方根为0.
(1)任何实数都只有1个立方根;
(2)正数的立方根为正数,负数的立方根为负数,0的立方根为0.
表示
求一个数a的立方根的运算叫做开立方,a叫做被开方数,可用符号表示为,读作“三次根号a”,中“3”叫做根指数.
数学语言:若,则.
例如:7的立方根为,的立方根为.
求一个数的立方根的运算,叫做开立方,开立方与立方互为逆运算.
重要性质
(1)在式子中,a为任何实数;(2);.
初一数学.春季..直升班.教师版.第8讲 全等复习: 这是一份初一数学.春季..直升班.教师版.第8讲 全等复习,共20页。
初一数学.春季.直升班.教师版.第7讲 分式(二): 这是一份初一数学.春季.直升班.教师版.第7讲 分式(二),共20页。
初一数学.春季.直升班.教师版.第5讲 直角三角形: 这是一份初一数学.春季.直升班.教师版.第5讲 直角三角形,共20页。












