【精品讲义】人教版 九年级下册寒假同步课程（培优版）2反比例函数与几何综合.学生版

模块一  反比例函数的几何意义

1.反比例函数的几何意义：如图，在反比例函数图象上任选一点，向两坐标轴作垂线，垂线与坐标轴所围成矩形的面积为。如图二，所围成三角形的面积为

2.如图，四条双曲线、、、对应的函数解析式分别为：、、、，那么、、、的大小顺序为

☞ 利用k的几何意义求参数的数值或比较参数大小

【例1】         如图，点在反比例函数的图像上，过点作轴于点，作轴于点，矩形的面积为9，则该反比例函数的解析式为                

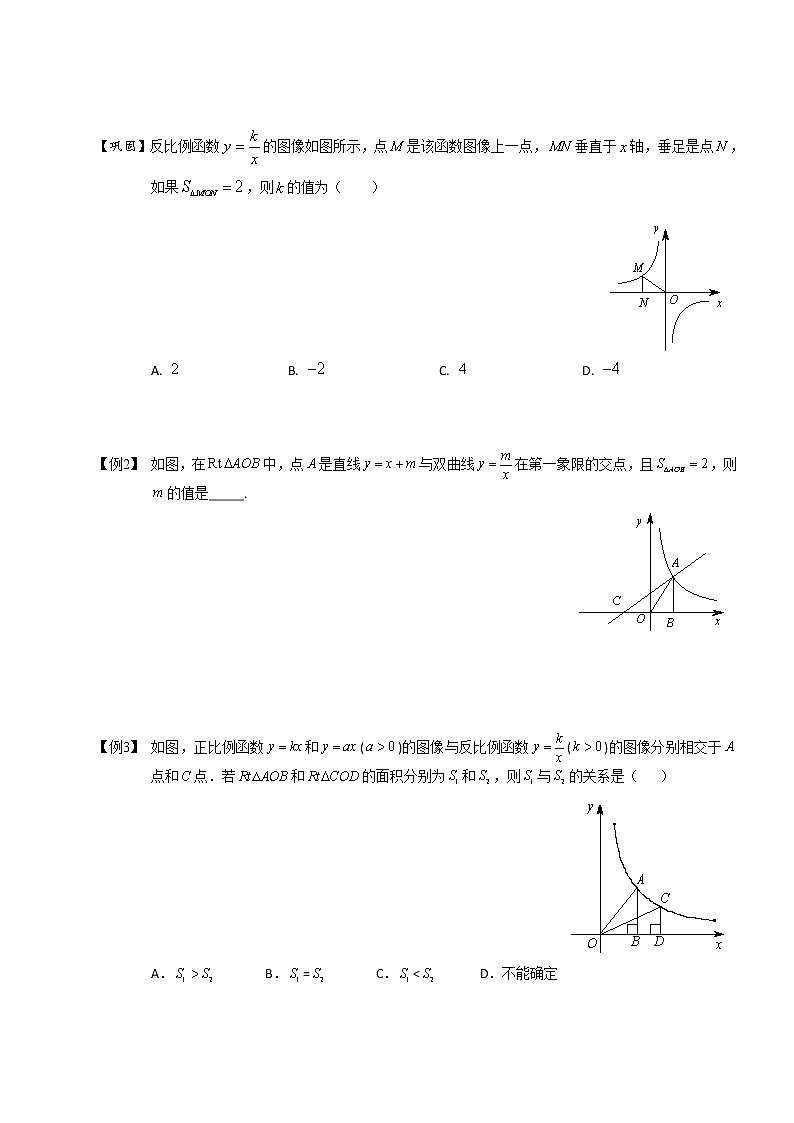
【巩固】反比例函数的图像如图所示，点是该函数图像上一点，垂直于轴，垂足是点，如果，则的值为（    ）

A.                B.                 C.                 D.

【例2】         如图，在中，点是直线与双曲线在第一象限的交点，且，则的值是_____.

【例3】         如图，正比例函数和()的图像与反比例函数()的图像分别相交于点和点．若和的面积分别为和，则与的关系是（   ）

A．       B．=       C．<      D．不能确定

【巩固】在函数()的图像上取三点、、，由这三点分别向轴、轴作垂线，设矩形、、的面积分别为、、，试比较三者大小.

【例4】         如图是三个反比例函数、、在轴上方的图象，由此观察得到、、的大小关系为          

☞ 反比例函数与方程的思想

【例5】         已知点在函数()的图像上，矩形的边在轴上，是对角线的 中点，函数()的图像经过、两点，若，求点的坐标.

模块二  反比例函数与面积的综合

1.若所求图形面积是规则图形，则可以按照相应图形的面积公式直接计算

2.若所求图形面积是不规则图形，则采用割补法

3.转化面积时，注意观察是否需要使用反比例函数的几何意义

☞ 一般面积问题

【例6】         在平面直角坐标系中，函数(，常数)的图象经过点(1，2)，(，)，()，过点作轴的垂线，垂足为．若的面积为2，求点的坐标．

【巩固】如图，直线与反比例函数的图象相交于点、点，与轴交于点，其中点的坐标为，点的横坐标为．

（1）试确定反比例函数的关系式；

（2）求的面积．

【例7】         如图，点、是双曲线上的点，分别经过、两点向轴、轴作垂线段，若，则=         

【巩固】如图，在反比例函数()的图象上，有点，，，它们的横坐标依次为1，2，3，4．分别过这些点作轴与轴的垂线，图中所构成的阴影部分的面积从左到右依次为，，，求．

【巩固】已知是反比例函数图象上五个整数点（横、纵坐标均为整数），分别以这些点向横轴或纵轴作垂线段，由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图5所示的五个橄榄形，则这五个橄榄形的面积总和是        （用含π的代数式表示）

【例8】         如图，已知正方形的面积为9，点为坐标原点，点在轴上，点在轴上，点在函数(，)的图像上，点(，)为其双曲线上的任一点，过点分别作轴、轴的垂线，垂足分别为、，并设矩形和正方形不重合部分的面积为．

        ⑴求点的坐标和的值；

        ⑵当时，求点坐标；

        ⑶写出关于的函数关系式．

【巩固】如图，反比例函数的图象过矩形的顶点，、分别在轴、轴的正半轴上，．

（1）设矩形的对角线交于点，求出点的坐标；

（2）若直线平分矩形面积，求的值．

☞ 利用k的几何意义进行面积转化

1.如图，直线与反比例函数（）交于、两点，与、轴的交点分别为、，

那么，此方法是绝大部分学生选用的方法。但是，从效率来讲，就比较低

2.如图，过点、作轴的垂线，垂足分别为、，则根据的几何意义可得，，而，所以，此方法的好处，在于方便，快捷，不易出错。

【例9】         如图，在轴的正半轴上依次截取，过点分别作轴的垂线与反比例函数的图象相交于点，得直角三角形并设其面积分别为，则的值为          ．

【例10】     两个反比例函数和在第一象限内的图象如图所示，点在的图象上，轴于点，交的图象于点，轴于点，交的图象于点，当点在的图象上运动时，以下结论：

①与的面积相等；

②四边形的面积不会发生变化；

③与始终相等；

④当点是的中点时，点一定是的中点．

其中一定正确的是            （把你认为正确结论的序号都填上，少填或错填不给分）．

【巩固】如图，点、在反比例函数()的图象上，且点、的横坐标分别为和()轴，垂足为，的面积为．

（1）求反比例函数的解析式；

（2）若点(，)，(，)也在反比例函数的图象上，试比较与的大小；

（3）求的面积．

【巩固】如图，已知双曲线经过直角三角形斜边的中点，与直角边相交于点．若的面积为，则__________．

☞ k的几何意义与双曲线的对称性

1.如图一，直线与反比例函数（）交于、两点，与、轴的交点分别为、，

那么，此两种方法是绝大部分学生选用的方法。常规方法，费时、费力、而且还易计算出错。

2.如图二，我们知道反比例函数的图象是双曲线，关于原点成中心对称，那么延长交双曲线于点，连接、则，，因此可以将的面积转化为梯形的面积

【例11】     直线（）与双曲线交于、两点，则的值等于      

【例12】     如图，一次函数的图像与反比例函数的图像交于两点．

（1）试确定上述反比例函数和一次函数的表达式；

（2）求的面积．

【巩固】已知反比例函数上两点，的横坐标分别为，，则的面积为       

模块三  反比例函数与其他几何问题

☞反比例函数与等腰三角形

1.涉及一般等腰三角形存在性的问题，注意需要分类讨论，

2.如果有等腰直角三角形或者等边三角形，注意考虑它的特殊性质

【例13】     如图，已知反比例函数的图象与一次函数的图象交于两点，．

（1）求反比例函数和一次函数的解析式；

（2）在轴上是否存在点，使为等腰三角形？若存在，请你直接写出点的坐标；若不存在，请说明理由．

【例14】     如图，、都是等腰直角三角形，点、在函数()的图像上，斜边、、都在轴上，求点的坐标.

【巩固】如图所示，，……，在函数的图象上，，，，…，，…都是等腰直角三角形，斜边都在轴上，则______________．

1.                    如图，已知一次函数的图象与反比例函数的图象交于、两点，且点的横坐标和点的纵坐标都是

⑴求一次函数解析式

⑵的面积

2.                    如图，正方形，的顶点、、在坐标轴上，点在上，点、在函数的图象上，则点的坐标是            

1．   已知反比例函数和一次函数，其中一次函数的图象经过、两点

⑴求反比例函数的解析式

⑵如图，已知点在第一象限且同时在上述两个函数的图象上，求点坐标；

⑶利用⑵的结果，请问：在轴上是否存在点，使为等腰三角形？若存在，把符合条件的点坐标都求出来；若不存在，请说明理由。