人教版九年级下册26.1.1 反比例函数精品导学案

这是一份人教版九年级下册26.1.1 反比例函数精品导学案，共9页。学案主要包含了学习目标，知识网络，要点梳理，典型例题，总结升华，思路点拨，答案与解析等内容，欢迎下载使用。




【学习目标】


1．使学生理解并掌握反比例函数的概念，能根据实际问题中的条件确定反比例函数的解析式，能判断一个给定函数是否为反比例函数；


2．能描点画出反比例函数的图象，会用待定系数法求反比例函数的解析式；


3．能根据图象数形结合地分析并掌握反比例函数的性质，能利用这些性质分析和解决一些简单的实际问题.


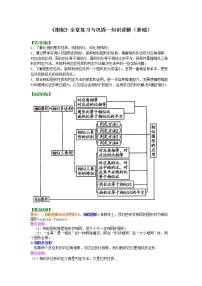
【知识网络】





【要点梳理】


要点一、反比例函数的概念


一般地，形如 (为常数，)的函数称为反比例函数，其中是自变量，是函数，自变量的取值范围是不等于0的一切实数.


要点诠释：在中，自变量的取值范围是， ()可以写成()的形式，也可以写成的形式.


要点二、反比例函数解析式的确定


反比例函数解析式的确定方法是待定系数法.由于反比例函数中，只有一个待定系数，因此只需要知道一对的对应值或图象上的一个点的坐标，即可求出的值，从而确定其解析式.


要点三、反比例函数的图象和性质


1.反比例函数的图象


反比例函数的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限．它们关于原点对称，反比例函数的图象与轴、轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远不与坐标轴相交．


要点诠释：


观察反比例函数的图象可得：和的值都不能为0，并且图象既是轴对称图形，又是中心对称图形，它有两条对称轴，对称中心是坐标原点．


①的图象是轴对称图形，对称轴为两条直线；


②的图象是中心对称图形，对称中心为原点（0，0）；


③(k≠0)在同一坐标系中的图象关于轴对称，也关于轴对称.





注：正比例函数与反比例函数，


当时，两图象没有交点；当时，两图象必有两个交点，且这两个交点关于原点成中心对称.





2.反比例函数的性质


（1）图象位置与反比例函数性质


当时，同号，图象在第一、三象限，且在每个象限内，随的增大而减小；当时，异号，图象在第二、四象限，且在每个象限内，随的增大而增大.


（2）若点()在反比例函数的图象上，则点（）也在此图象上，故反比例函数的图象关于原点对称.


（3）正比例函数与反比例函数的性质比较





（4）反比例函数y＝中的意义


①过双曲线(≠0) 上任意一点作轴、轴的垂线，所得矩形的面积为.


②过双曲线(≠0) 上任意一点作一坐标轴的垂线，连接该点和原点，所得三角形的面积为.





要点四、应用反比例函数解决实际问题须注意以下几点


1．反比例函数在现实世界中普遍存在，在应用反比例函数知识解决实际问题时，要注意将实际问题转化为数学问题.


2．列出函数关系式后，要注意自变量的取值范围.


【典型例题】


类型一、确定反比例函数的解析式


1、已知函数是反比例函数，则的值为 .


【答案】


【解析】根据反比例函数概念，＝且，可确定的值.


【总结升华】反比例函数要满足以下两点：一个是自变量的次数是－1，另一个是自变量的系数不等于0.


举一反三：


【变式】反比例函数图象经过点（2，3），则的值是（ ）.


A. B. C. 0D. 1


【答案】D；


反比例函数过点（2，3）．．


类型二、反比例函数的图象及性质


2、已知，反比例函数的图象在每个分支中随的增大而减小，试求的取值范围．


【思路点拨】由反比例函数性质知，当＞0时，在每个象限内随的增大而减小，由此可求出的取值范围，进一步可求出的取值范围．


【答案与解析】


解：由题意得：，解得，


所以，则＜3．


【总结升华】熟记并能灵活运用反比例函数的性质是解答本题的关键．


举一反三：


【变式】已知反比例函数，其图象位于第一、第三象限内，则的值可为________（写出满足条件的一个的值即可）．


【答案】3（满足＞2即可）.


3、在函数（，为常数）的图象上有三点(－3，)、(－2，)、(4，)，则函数值的大小关系是（ ）


A． B． C． D．


【答案】D；


【解析】


∵ ||＞0，∴ －||＜0，∴反比例函数的图象在第二、四象限，且在每一个象限里，随增大而增大，(－3，)、(－2，)在第二象限，(4，)在第四象限，∴ 它们的大小关系是：．


【总结升华】根据反比例函数的性质，比较函数值的大小时，要注意相应点所在的象限，不能一概而论，本题的点(－3，)、(－2，)在双曲线的第二象限的分支上，因为－3＜－2，所以，点(4，)在第四象限，其函数值小于其他两个函数值．


举一反三：


【变式1】（2014春•海口期中）在同一坐标系中，函数y=和y=kx+3（k≠0）的图象大致是（ ）.


A. B.


C. D.


【答案】C；


提示：分两种情况讨论：


①当k＞0时，y=kx+3与y轴的交点在正半轴，过一、二、三象限，y=的图象在第一、三象限；


②当k＜0时，y=kx+3与y轴的交点在正半轴，过一、二、四象限，y=的图象在第二、四象限．故选C．





【变式2】已知,且则函数与在同一坐标系中的图象不可能是( ) .





【答案】B ；


提示：因为从B的图像上分析，对于直线来说是，则，对于反比例函数来说，，所以相互之间是矛盾的，不可能存在这样的图形.


4、（2016•齐齐哈尔）如图，已知点P（6，3），过点P作PM⊥x轴于点M，PN⊥y轴于点N，反比例函数y=的图象交PM于点A，交PN于点B．若四边形OAPB的面积为12，则k= ．





【思路点拨】根据点P（6，3），可得点A的横坐标为6，点B的纵坐标为3，代入函数解析式分别求出点A的纵坐标和点B的横坐标，然后根据四边形OAPB的面积为12，列出方程求出k的值．


【答案】6．


【解析】


解：∵点P（6，3），


∴点A的横坐标为6，点B的纵坐标为3，


代入反比例函数y=得，


点A的纵坐标为，点B的横坐标为，


即AM=，NB=，


∵S四边形OAPB=12，


即S矩形OMPN﹣S△OAM﹣S△NBO=12，


6×3﹣×6×﹣×3×=12，


解得：k=6．


故答案为：6．


【总结升华】本题考查了反比例函数系数k的几何意义，解答本题的关键是根据点A、B的纵横坐标，代入解析式表示出其坐标，然后根据面积公式求解．


举一反三：


【变式】如图，过反比例函数的图象上任意两点A、B，分别作轴的垂线，垂足为，连接OA，OB，与OB的交点为P，记△AOP与梯形的面积分别为，试比较的大小.





【答案】


解：∵，


且，


∴.





类型三、反比例函数与一次函数综合


5、已知反比例函数和一次函数的图象的一个交点坐标是(－3，4)，且一次函数的图象与轴的交点到原点的距离为5，分别确定反比例函数和一次函数的表达式．


【思路点拨】因为点(－3，4)是反比例函数与一次函数的图象的一个交点，所以把(－3，4)代入中即可求出反比例函数的表达式．欲求一次函数的表达式，有两个待定未知数，已知一个点(－3，4)，只需再求一个一次函数图象上的点即可．由已知一次函数图象与轴的交点到原点的距离是5，则这个交点坐标为(－5，0)或(5，0)，分类讨论即可求得一次函数的解析式．


【答案与解析】


解：因为函数的图象经过点(－3，4)，


所以，所以＝－12．


所以反比例函数的表达式是．


由题意可知，一次函数的图象与轴的交点坐标为(5，0)或(－5，0)，则分两种情况讨论：


当直线经过点(－3，4)和(5，0)时，


有 解得


所以．


当直线经过点(－3，4)和(－5，0)时，


有 解得 所以．


所以所求反比例函数的表达式为，一次函数的表达式为或．


【总结升华】本题考查待定系数法求函数解析式，解答本题时要注意分两种情况讨论，不能漏解．


举一反三：


【变式】如图所示，A、B两点在函数的图象上．





（1）求的值及直线AB的解析式；


（2）如果一个点的横、纵坐标均为整数，那么我们称这个点是格点．请直接写出图中阴影部分（不包括边界）所含格点的个数．


【答案】


解：（1）由图象可知，函数的图象经过点A(1，6)，可得＝6．


设直线AB的解析式为．


∵ A(1，6)，B(6，1)两点在函数的图象上，


∴ 解得


∴ 直线AB的解析式为．


（2）题图中阴影部分(不包括边界)所含格点的个数是3．


类型四、反比例函数应用


6、（2015•兴化市三模）一辆客车从甲地出发前往乙地，平均速度v（千米/小时）与所用时间t（小时）的函数关系如图所示，其中60≤v≤120．


（1）直接写出v与t的函数关系式；


（2）若一辆货车同时从乙地出发前往甲地，客车比货车平均每小时多行驶20千米，3小时后两车相遇．


①求两车的平均速度；


②甲、乙两地间有两个加油站A、B，它们相距200千米，当客车进入B加油站时，货车恰好进入A加油站（两车加油的时间忽略不计），求甲地与B加油站的距离．





【答案与解析】


解：（1）设函数关系式为v=，


∵t=5，v=120，


∴k=120×5=600，


∴v与t的函数关系式为v=（5≤t≤10）；


（2）①依题意，得


3（v+v﹣20）=600，


解得v=110，


经检验，v=110符合题意．


当v=110时，v﹣20=90．


答：客车和货车的平均速度分别为110千米/小时和90千米/小时；


②当A加油站在甲地和B加油站之间时，


110t﹣（600﹣90t）=200，


解得t=4，此时110t=110×4=440；


当B加油站在甲地和A加油站之间时，


110t+200+90t=600，


解得t=2，此时110t=110×2=220．


答：甲地与B加油站的距离为220或440千米．


【总结升华】解决反比例函数与实际问题相结合的问题，要理解问题的实际意义及与之相关的数学知识.反比例函数是解决现实世界反比例关系的有力工具.
正比例函数
反比例函数
解析式
图 像
直线
有两个分支组成的曲线（双曲线）
位 置
，一、三象限；


，二、四象限
，一、三象限


，二、四象限
增减性
，随的增大而增大


，随的增大而减小
，在每个象限，随的增大而减小


，在每个象限，随的增大而增大