人教版七年级下册5.1 相交线综合与测试优秀当堂达标检测题

这是一份人教版七年级下册5.1 相交线综合与测试优秀当堂达标检测题，共10页。试卷主要包含了1《相交线》同步练习卷，5B．4等内容，欢迎下载使用。

一．选择题


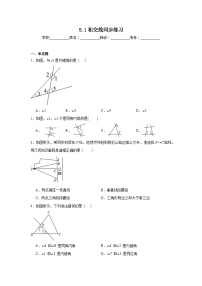
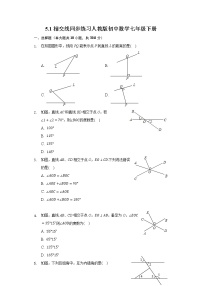
1．下列图中，∠1与∠2是同位角的是（ ）


A．B．C．D．


2．下列四个图形中，∠1和∠2是内错角的是（ ）


A．B．C．D．


3．如图，∠1，∠2是对顶角的是（ ）


A．B．C．D．


4．如图，直线b、c被直线a所截，则∠1与∠2是（ ）





A．内错角B．同位角C．同旁内角D．对顶角


5．如图，直线AB、CD相交于点O，OE平分∠AOD，若∠1＝38°，则∠COE等于（ ）





A．66°B．76°C．109°D．144°


6．如图所示，在△ABC中，AE⊥BD，点A到直线BD的距离指（ ）





A．线段AB的长B．线段AD的长C．线段ED的长D．线段AE的长


7．如图，点P是直线a外一点，A，B，C，D都在直线上，PB⊥α于B，下列线段最短的是（ ）





A．PAB．PCC．PBD．PD


8．如图，AC⊥BC，AC＝4，点D是线段BC上的动点，则A、D两点之间的距离不可能是（ ）





A．3.5B．4.5C．5D．5.5


9．如图，AC⊥BC，直线EF经过点C，若∠1＝35°，则∠2的大小为（ ）





A．65°B．55°C．45°D．35°


10．如图，直线AB、CD相交于点O，OE平分∠AOC，若∠BOD＝70°，则∠COE的度数是（ ）





A．70°B．50°C．40°D．35°


二．填空题（共8小题）


11．如图，∠B的内错角是 ．





12．联结直线外一点与直线上各点的所有连线中， 最短．


13．如图，∠1与∠2是直线 和 被直线 所截的一对 角．





14．如图，直角三角形ABC中，AC⊥BC，CD⊥AB，点A到直线BC的距离等于线段 的长度，点A到直线CD的距离等于线段 的长度．





15．如图，已知AO⊥BC于O，∠BOD＝120°，那么∠AOD＝ °．





16．如图，直线a、b相交，∠1＝36°，则∠2﹣∠3＝ ．





17．∠1＝75°，则∠1的邻补角的邻补角等于 ．


18．平面内有a、b、c三条直线，则它们的交点个数可能是 个．


三．解答题（共6小题）


19．如图所示，码头、火车站分别位于A，B两点，直线a和b分别表示铁路与河流．


（1）从火车站到码头怎样走最近，画图并说明理由；


（2）从码头到铁路怎样走最近，画图并说明理由；


（3）从火车站到河流怎样走最近，画图并说明理由．








20．如图所示，已知∠1＝115°，∠2＝65°，∠3＝100°．


（1）图中所有角中（包含没有标数字的角），共有几对内错角？


（2）求∠4的大小．








21．复杂的数学问题我们常会把它分解为基本问题来研究，化繁为简，化整为零这是一种常见的数学解题思想．


（1）如图1，直线l1，l2被直线l3所截，在这个基本图形中，形成了 对同旁内角．


（2）如图2，平面内三条直线l1，l2，l3两两相交，交点分别为A、B、C，图中一共有 对同旁内角．


（3）平面内四条直线两两相交，最多可以形成 对同旁内角．


（4）平面内n条直线两两相交，最多可以形成 对同旁内角．





22．观察下列图形，阅读下面的相关文字并回答以下问题：


两条直线相交三条直线相交四条直线相交


只有一个交点最多的3个交点最多有6个交；


猜想：①5条直线相交最多有几个交点？


②6条直线相交最多有几个交点？


③n条直线相交最多有几个交点？





23．如图，已知直线AB与CD相交于点O，∠BOC＝∠AOC，∠BOM＝80°，ON平分∠DOM，求∠BOC和∠MON．
































24．如图，直线AB，CD相交于点O，OD平分∠BOE，OF平分∠AOE．


（1）证明：OD⊥OF．


（2）若∠BOD＝28°，找出∠BOD的补角，并求出∠BOF的度数．























参考答案


一．选择题


1．解：选项A中的两个角是同旁内角，因此不符合题意；


选项C中的两个角既不是同位角、也不是内错角、同旁内角，因此不符合题意；


选项D不是两条直线被一条直线所截出现的角，不符合题意；


只有选项B中的两个角符合同位角的意义，符合题意；


故选：B．


2．解：A、∠1与∠2不是内错角，选项错误，不符合题意；


B、∠1与∠2不是内错角，选项错误，不符合题意；


C、∠1与∠2是内错角，选项正确，符合题意；


D、∠1和∠2不是内错角，选项错误，不符合题意；


故选：C．


3．解：根据对顶角的定义，只有选项C的图形符合题意．


故选：C．


4．解：直线b、c被直线a所截，则∠1与∠2是同位角，


故选：B．


5．解：∵∠1＝38°，


∴∠AOD＝180°﹣∠1＝142°，


∵OE平分∠AOD，


∴∠DOE＝∠AOD＝71°，


∴∠COE＝180°﹣∠DOE＝109°，


故选：C．


6．解：点A到直线BD的距离指线段AE的长，


故选：D．


7．解：由题意，得


点P是直线a外一点，A，B，C，D都在直线上，PB⊥α于B，下列线段最短的是PB，


故选：C．


8．解：∵AC⊥BC，AC＝4，


∴AD≥AC，即AD≥4．


观察选项，只有选项A符合题意．


故选：A．


9．解：∵AC⊥BC，


∴∠ACB＝90°，


∵∠1+∠ACB+∠2＝180°，


∴∠2＝180°﹣90°﹣35°＝55°，


故选：B．


10．解：∵∠BOD＝70°，


∴∠AOC＝∠BOD＝70°，


∵OE平分∠AOC，


∴∠COE＝∠AOC＝×70°＝35°，


故选：D．


二．填空题（共8小题）


11．解：∠B的内错角是∠BAD；


故答案为：∠BAD．


12．解：联结直线外一点与直线上各点的所有连线中，垂线段最短，


故答案为：垂线段．


13．解：∠1与∠2是直线a和b被直线c所截的一对内错角．


故答案为：a；b；c；内错．


14．解：直角三角形ABC中，AC⊥BC，CD⊥AB，点A到直线BC的距离等于线段AC的长度，点A到直线CD的距离等于线段AD的长度．


故答案为：AC；AD．


15．解：∵AO⊥BC，


∴∠AOB＝90°，


∵∠BOD＝120°，


∴∠AOD＝∠BOD﹣∠AOB＝120°﹣90°＝30°，


故答案是：30．


16．解：∵直线a、b相交，∠1＝36°，


∴∠3＝∠1＝36°，∠2＝180°﹣∠1＝144°，


∴∠2﹣∠3＝144°﹣36°＝108°．


故答案为：108°．


17．解：如果∠1＝75°，那么∠1的邻补角的邻补角等于∠1，就是75°，


故答案为：75°．


18．解：因为三条直线位置不明确，所以分情况讨论：


①三条直线互相平行，有0个交点；


②一条直线与两平行线相交，有2个交点；


③三条直线都不平行，有1个或3个交点；


所以交点个数可能是0、1、2、3．


故答案为：0、1、2、3．


三．解答题（共6小题）


19．解：如图所示


（1）沿AB走，两点之间线段最短；


（2）沿AC走，垂线段最短；


（3）沿BD走，垂线段最短．





20．解：如图所示：





（1）直线c和d被直线b所截，有两对内错角，


即∠2和∠6，∠5和∠7，


同理还有六对内错角，


共有8对内错角；


（2）∵∠2+∠5＝180°，∠2＝65°，


∴∠5＝180°﹣65°＝115°，


∵∠1＝115°，


∴∠1＝∠5，


∴a∥b，


∴∠3＝∠6，


又∵∠3＝100°，


∴∠6＝100°，


∴∠4＝∠6＝100°．


21．解：（1）直线l1，l2被直线l3所截，在这个基本图形中，形成了2对同旁内角．


（2）平面内三条直线l1，l2，l3两两相交，交点分别为A、B、C，图中一共有6对同旁内角．


（3）平面内四条直线两两相交，最多可以形成24对同旁内角．


（4）平面内n条直线两两相交，最多可以形成n（n﹣1）（n﹣2）对同旁内角


故答案为：（1）2；（2）6；（3）24；（4）n（n﹣1）（n﹣2）


22．解：①5条直线相交最多有＝10个交点；


②6条直线相交最多有＝15个交点；


③n条直线相交最多有个交点．


23．解：∵∠BOC＝∠AOC，


∴∠AOC＝5∠BOC


∵∠BOC+∠AOC＝180°，


∴∠BOC＝30°，


∵∠AOD与∠BOC是对顶角，


∴∠AOD＝∠BOC＝30°，


∵∠BOM＝80°，


∴∠COM＝∠BOM﹣∠BOC＝50°，


∴∠DOM＝180°﹣∠COM＝130°，


∵ON平分∠DOM，


∴∠MON＝∠DOM＝65°．


答：∠BOC为30°；∠MON为65°．





24．证明：（1）∵OD平分∠BOE，OF平分∠AOE，


∴∠EOF＝∠AOE，∠EOD＝∠EOB，


∵∠AOE+∠EOB＝180°，


∴∠FOD＝∠EOF+∠EOD＝90°，


∴OD⊥OF；


（2）∵∠BOD＝28°，


∴∠AOD＝180°﹣∠BOD＝180°﹣28°＝152°，


∵OD平分∠BOE，


∴∠EOD＝∠BOD，


∴∠COE＝180°﹣∠EOD＝180°﹣28°＝152°，


∴∠BOD的补角是∠COE和∠AOD，


∵∠FOD＝90°，


∴∠BOF＝∠DOF+∠BOD＝90°+28°＝118°．