初中数学青岛版九年级下册第5章 对函数的再探索5.4二次函数的图像与性质备课ppt课件

这是一份初中数学青岛版九年级下册第5章 对函数的再探索5.4二次函数的图像与性质备课ppt课件，共36页。PPT课件主要包含了运动场上飞舞的跳绳，奥运赛场腾空的篮球，3二次函数，温故而知新，自学探究，a≠0，合作交流，任意实数，二次函数的一般形式，例题讲解等内容，欢迎下载使用。

1.探索并归纳二次函数的定义；2.能写出一些简单函数的解析式并会判断是否是二次函数。
请用适当的解析式表示下列问题情境中的两个变量 y 与 x 之间的关系·
（2）一个小球由静止开始沿斜坡向下滚动，5s时到达斜坡底部.测得小球滚动的距离s(cm)与时间t(s)的数据如下表：
(3)某企业去年的产值为1200万元.如果三年内该企业年产值平均每年的增长率为x,你能写出明年该企业年产值y(万元)与x之间的函数表达式.
y = 1200(1+x)+1200(1+x)x =
这些关系中y是x的什么函数？
上述三个问题中的函数解析式具有哪些共同的特征?
经化简后都具有y=ax²+bx+c 的形式.
(a,b,c是常数, )
定义：一般地，形如y=ax²+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数。其中：a为二次项系数， b为一次项系数，c为常数项.
（1）等号左边是变量y，右边是关于自变量x的
（2）等式的右边最高次数为 。
（3）a,b,c为常数，且
（4）x的取值范围是 。
(可以没有一次项和常数项，但不能没有二次项。)
y＝ax2＋bx＋c (其中a、b、c是常数,a≠0)二次函数的特殊形式：当b＝0时， y＝ax2＋c当c＝0时， y＝ax2＋bx当b＝0，c＝0时， y＝ax2
判断一个函数是否是二次函数，看它是否化简成y=ax2+bx+c（a、b、c为常数且a≠0）的形式。
（8）y=x-2+x（ ）
1.下列函数中,哪些是二次函数？
(1）y=3(x-1)²+1;
(3) s=3-2t².
(5)y=(x+3)²-x².
(6) v=10πr²
(7) y= x²+x³+25
2.写出二次函数的二次项系数、一次项系数和常数项：
写出下列各函数关系，并判断它们是什么类型的函数（1）写出正方体的表面积S（cm2）与正方体的棱长a（cm）之间的函数关系；（2）写出圆的面积y（cm2）与它的周长x（cm）之间的函数关系；（3）菱形的两条对角线的和为26cm，写出菱形的面积S（cm2）与一对角线长x（cm）之间的函数关系．
（2）由题意得 ，其中y是x的二次函数；
（3）由题意得 ，其中S是x的二次函数.
【解析】 （1）由题意得 ，其中S是a的二次函数；
2.矩形的长是4厘米，宽是3厘米，如果将其长增加x厘米，其宽增加2x厘米,则面积增加到y平方厘米，试写出y与x的关系式．
【解析】 y=(4+x)(3+2x)= 2x2+11x+12
1.二次函数y=-6x2+4x-2的二次项系数、一次项系数、常数项分别是多少？【解析】二次项系数是-6，一次项系数是4，常数项是-2.
（2）m取什么值时，此函数是正比例函数？
（3）m取什么值时，此函数是反比例函数？
已知函数y=( - k )x2 +kx+ (1) k为何值时，y是x的一次函数？ (2)k为何值时，y是x的二次函数？
2、函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )A、m,n是常数,且m≠0 B、m,n是常数,且n≠0C、m,n是常数,且m≠n D、m,n为任何实数
3.若函数 为二次函数，求m的值.
解①得：m=2或m=-1;
解②得：m≠1且m≠-1;
【解析】因为该函数为二次函数， 则
m2—2m-1=2 m+1 ≠0 ∴m=3
4:m取何值时， 函数 是二次函数？
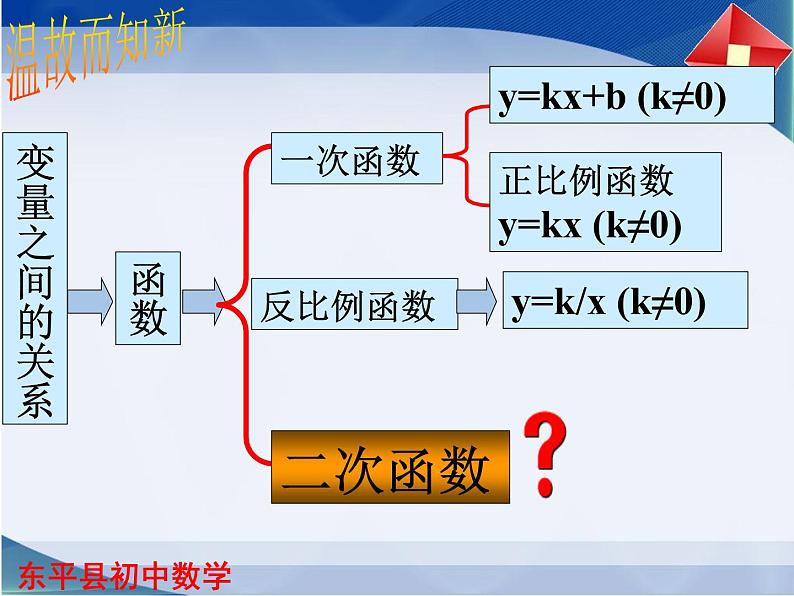
一次函数y=kx+b (k ≠0),其中包括正比例函数 y=kx(k≠0), 反比例函数y= (k≠0) ， 二次函数y=ax2+bx+c(a≠0)。
现在我们学习过的函数有:
可以发现,这些函数的名称都形象地反映了函数表达式与自变量的关系。
解：（１）当m2－7=1且m+3≠0即m=± 　时是正比例函数。
（２）当m2－7=-1且m+3≠0即m=± 时是反比例函数。
（３）当m2－7=2且m+3≠0即m=3时是二次函数。
2.如果函数y=(k-3) +kx+1是二次函数,则k的值一定是______.
1.如果函数y= +kx+1是二次函数,则k的值一定是______.

　　用20米的篱笆围一个矩形的花圃（如图），设连墙的一边为x,矩形的面积为y,求：(1)写出y关于x的函数关系式.(2)当x=3时,矩形的面积为多少?
2.函数 y=(m-n)x2+ mx+n 是二次函数的条件是( )A m,n是常数,且m≠0 B m,n是常数,且n≠0C m,n是常数,且m≠n D m,n为任何实数
3.下列函数中，哪些是二次函数？(1) y=5x+1；(2) y=4x2-1；(3)y=-(x-1)2；(4)y=(x+2)2-x2.
【解析】根据次数的要求可以排除哪些函数不是二次函数？答：(1)，(4) .哪些是二次函数?答：(2)，(3) .
4.某工厂计划为一批长方体形状的产品涂上油漆,长方体的长和宽相等,高比长多0.5 m.(1)长方体的长和宽用x(m)表示,长方体需要涂漆的表面积S(m2)如何表示?(2)如果涂漆每平米所需要的费用是5元,涂漆每个长方体所需要的费用用y(元)表示,那么y的表达式是什么?
解析：（1）S=2x2+x(x+0.5)×4=6x2+2x；
（2）y=5S=5×(6x2+2x) ∴y=30x2+10x.
5.体育课上，老师用绳子围成一个周长为30米的游戏场地，围成的场地是如图所示的矩形ABCD．设边AB的长为x（单位：米），矩形ABCD的面积为S（单位：平方米）.（1）求S与x之间的函数关系式（不要求写出自变量x的取值范围）；（2）若矩形ABCD的面积为50平方米，且AB＜AD，请求出此时AB的长.
解析：（1）S=x(15-x)=-x2+15x ；（2）由题意：-x2+15x＝50，解得：x1＝5，x2=10，∵AB＜AD，∴AB＝5米.
一农民用40m长的篱笆围成一个一边靠墙的长方形菜园，和墙垂直的一边长为Xm，菜园的面积为Ym2，求y与x之间的函数关系式，并说出自变量的取值范围。当x=12m时，计算菜园的面积。
（40-2x ）m
Y=x(40-2x)
即：Y=-2x2+40x
当x＝12m时，菜园的面积为：
Y=-2x2+40x＝-2×122+40×12 ＝192（m2）