初中数学冀教版八年级下册22.7 多边形的内角和与外角和图片ppt课件

这是一份初中数学冀教版八年级下册22.7 多边形的内角和与外角和图片ppt课件，共26页。PPT课件主要包含了看一看，多边形，了解一下，多边形的内角和，巩固练习一，巩固练习二，巩固练习三，n-3，猜想与说理，多边形的外角和等内容，欢迎下载使用。

小明有一个设想：2008年奥运会在北京召开，要是能设计一个内角和是2008°的多边形花坛该多有意义啊！小明的这个想法能实现吗？
22.7多边形的 内角和与外角和
学习目标：1、了解多边形的定义，多边形的顶点、边、内角、外角及对角线等概念。2、探索求多边形的内角和，外角和的方法3、会应用多边形内角和与外角和公式解决问题
平面上，由不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
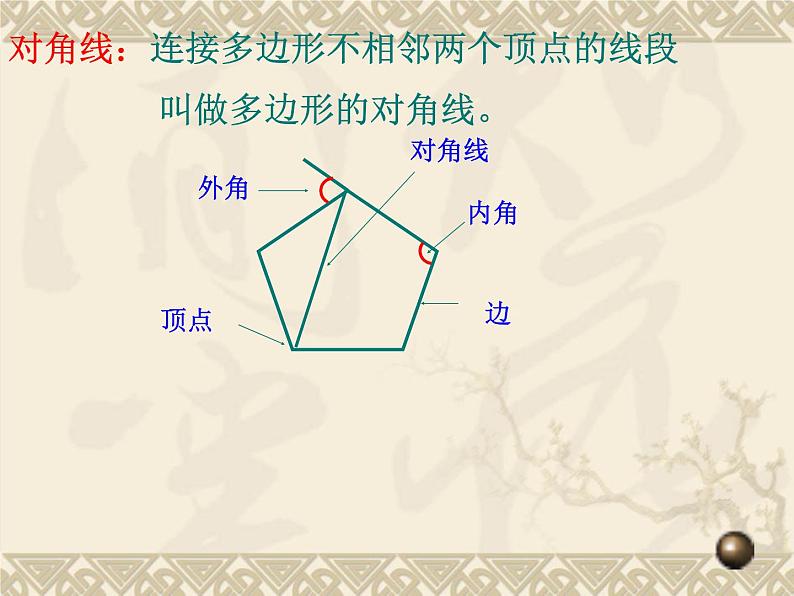
对角线：连接多边形不相邻两个顶点的线段 叫做多边形的对角线。
利用三角形知识探索四边形内角和等于多少度？你能想到几种办法？
活动计划 1 .四人小组合作，在纸上完成四边形的分割．2 . 探究不同的分割方式所得到的四边形内角和．
注意事项1 . 用直尺作图，分割线条用虚线“ ”表示．2 . 尽可能多地想出不同的方法求其内角和．
答：十五边形的内角和是23400
例：求十五边形内角和的度数。
解：（n-2）×1800
=（15-2)×1800
n边形的内角和等于n边形一个顶点出发可引 条对角线则n个顶点的n边形共有 条对角线
（n-2）×180°（n≥3）
1、七边形内角和为（ ）
2、十七边形内角和为（ ）
3、八边形内角和为（ ）
1、多边形内角和为1260°则它是（ ）边形。
2、多边形内角和为1800°则它是（ ）边形。
1、十边形的对角线有（ ）条。
2、n（n≥3）边形从一个顶点出发有（ ）条对角线。
n边形的外角和是多少度呢?
n边形的外角和等于360°.
多边形的外角和等于360°
例：已知一个多边形，它的内角和与外角和相等。请说明这个多边形是几边形。
解：设多边形的边数为n，则它的内角和等于(n-2)×180°，外角和等于360 °.由(n-2)×180°= 360 °，解得n=4.所以这个多边形是四边形。
1、一个十边形的每一个内角都相等，那么这个十边形的每一外角等于( )A、144° B、 72 ° C、 36° D 、18°2、一个多边形每一个外角都等于45°，则这个多边形的内角和等于( )A、 720° B、 675° C、 1080°D、945°
例：如图，小亮从点O处出发，前进5m后向右转20°，在前进5m后又向右转20°，这样走n次恰好回到点O处。（1）小亮走出的这个n边形的每个内角是多少度？内角和是多少度？（2）小亮走出的这个n边形的周长是多少？
1、小明有一个设想：2008年奥运会在北京召开，要是能设计一个内角和是2008°的多边形花坛该多有意义啊！小明的这个想法能实现吗？
2、如图所示的模板,按规定AB,CD的延长线相交成80°的角, 因交点不在板上, 不便测量，质检员测得∠BAE=122°，∠DCF=155°. 如果你是质检员,如何知道模板是否合格?为什么?
定义：平面上，由不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。
1、十边形的内角和等于 。2、一个多边形的每一个外角都等于30°，则这个多边形为 边形。3、内角和为1440°的多边形是 。4、内角和等于外角和的多边形是 边形。5、五边形ABCDE中，若∠A = ∠D = 90°，∠B:∠C :∠E = 3:8:7，求∠B,∠C ,∠E的度数。
活动一：探索四边形内角和