初中数学冀教版八年级下册20.2 函数图片课件ppt

这是一份初中数学冀教版八年级下册20.2 函数图片课件ppt，共19页。PPT课件主要包含了1函数，指导教师朱会兰，根据上图填表，观察与感受，思考与感受，归纳与概括，操作与感受，操作与探究，问题一，问题二等内容，欢迎下载使用。

保定市第十三中学 张艳飞
O 1 2 3 4 5 6 7 8 9 10 11 12
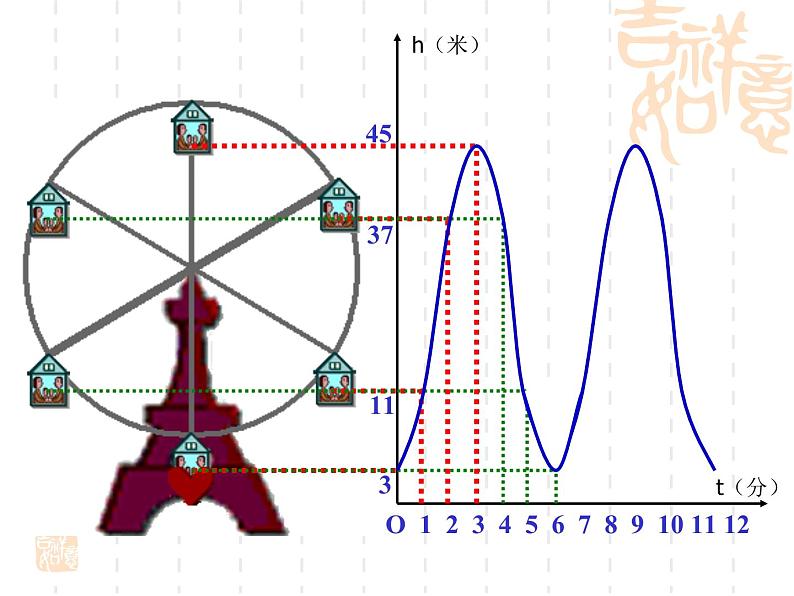
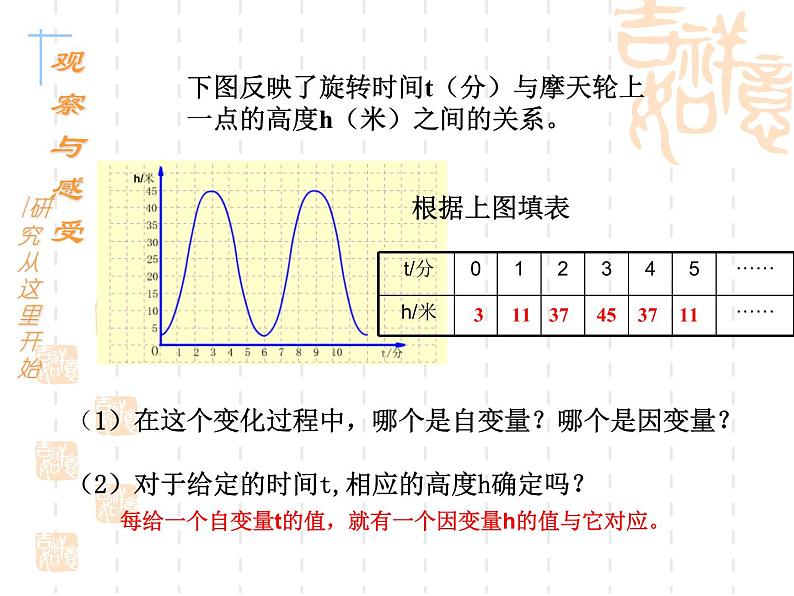
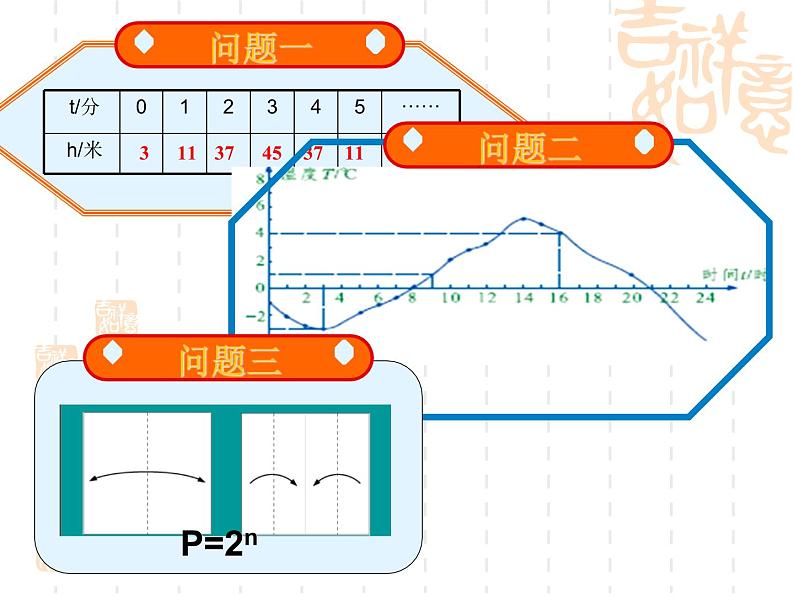
下图反映了旋转时间t（分）与摩天轮上一点的高度h（米）之间的关系。
（1）在这个变化过程中，哪个是自变量？哪个是因变量？（2）对于给定的时间t,相应的高度h确定吗？
每给一个自变量t的值，就有一个因变量h的值与它对应。
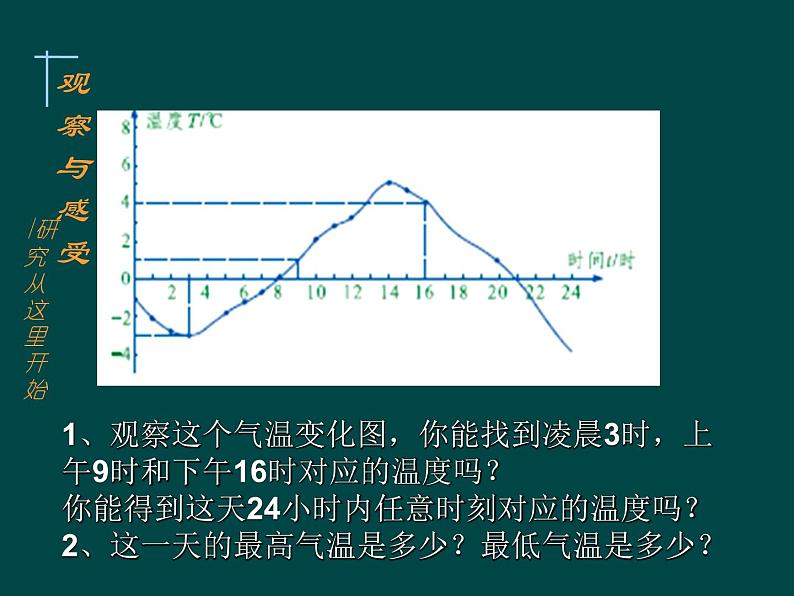
1、观察这个气温变化图，你能找到凌晨3时，上午9时和下午16时对应的温度吗？你能得到这天24小时内任意时刻对应的温度吗？2、这一天的最高气温是多少？最低气温是多少？
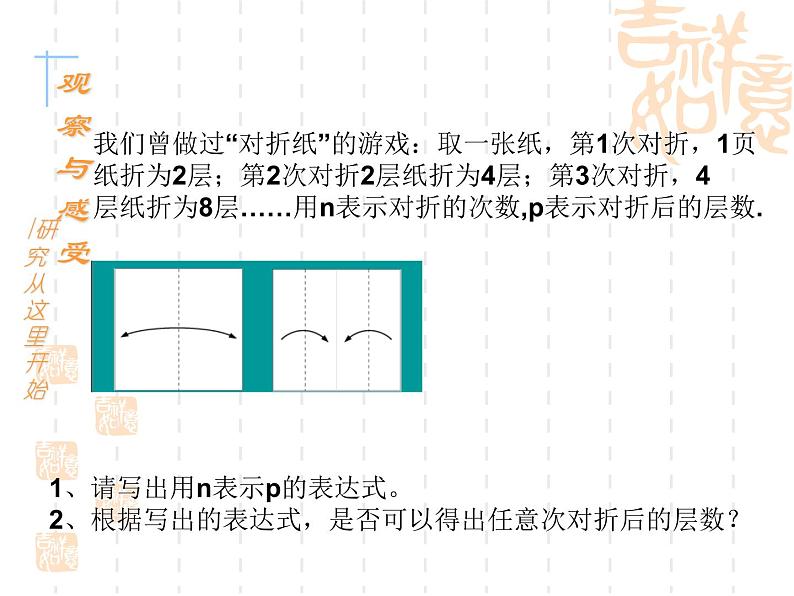
我们曾做过“对折纸”的游戏：取一张纸，第1次对折，1页纸折为2层；第2次对折2层纸折为4层；第3次对折，4层纸折为8层……用n表示对折的次数,p表示对折后的层数.
1、请写出用n表示p的表达式。2、根据写出的表达式，是否可以得出任意次对折后的层数？
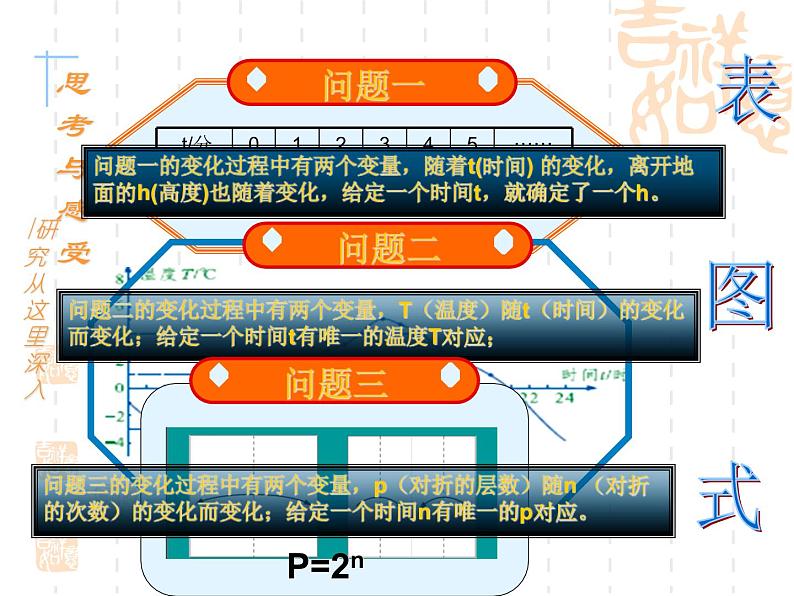
问题一的变化过程中有两个变量，随着t(时间) 的变化，离开地面的h(高度)也随着变化，给定一个时间t，就确定了一个h。
问题二的变化过程中有两个变量，T（温度）随t（时间）的变化而变化；给定一个时间t有唯一的温度T对应；
问题三的变化过程中有两个变量，p（对折的层数）随n （对折的次数）的变化而变化；给定一个时间n有唯一的p对应。
找出变化过程的共同点：
在上面各例中，都有两个变量，给定其中某一个变量（自变量）的值，相应地就确定了另一个变量（因变量）的值。
（1）两个变量；（2）一个量随着另一个量的变化而变化；（3）一个变量取一个定值时，另一个变量就有确定的值与之对应。
抽象概念： 一般地，如果在一个变化过程中有两个变量x和y，并且对于变量x的每一个值，变量y都有唯一的值与它对应，那么我们称y是x的函数，其中x是自变量。
1、下表给出了某年4月24日至5月7日两周时间内某种疫情的数据：
表中反映的两个量之间是否具有函数关系？如果具有函数关系，那么我们可将其中哪个变量看做另一个变量的函数？2、在△ABC，BC=8.如果BC边上的高AH=x在发生变化，那么△ABC的面积 在这个问题中，变量有 、 ，其中， 可以看成 的函数。3、从A地向B地打长途电话，按时收费，3分钟内收费2.4元，3分钟后，每增加1分钟多收1元，某人从A地向B地打电话共用了t（t≥3,t为整数）分钟，话费为m元，请写出m与t之间的函数关系式。
1、某市某一天的气温T（温度）是t（时间）的函数，其中自变量t可取哪些值?如果t取第二天凌晨3时,原问题还有意义吗?
2、折纸的层数是折纸次数的函数，其中自变量n可取哪些值?当n=0.5时,原问题有没有意义?
函数的自变量可以在允许的范围内取值，超出这个范围可能失去意义，这就是函数的自变量的取值范围问题。
解答：（1）x取任意实数（2）x≠0 (3) x≥-1
函数的自变量的取值范围由哪些条件确定。
2、如图，等腰直角三角形ABC的直角边长与正方形MNPQ的边长均10cm , 边CA与边MN 在同一条直线上,点A与点M重合.让△ABC沿MN方向运动.当点A与点N 重合时停止运动.试写出运动中两个图形重叠部分的面积y(cm2) 与MA 的长度x(cm)之间的函数关系式,并指出自变量的取值范围.
解:因为△ABC是等腰直角三角形, 四边形MNPQ是正方形,且AB=BC=QM=MN,所以运动中两个图形的重叠部分也是等腰直角三角形，由MA=x,得
结合1、2题分析函数的自变量的取值范围由那些条件确定。
一是使函数表达式有意义；二是使所描述的实际问题有意义。
1、在刚刚的数学活动中， 我们一起研究了哪些问题？
2、在刚刚的数学活动中， 我们一起经历了怎样的过程？
3、在刚刚的数学活动中， 你们有什么感受体会？
1、函数概念2、两个变量成为函数关系的依据3、函数自变量的取值范围的确定
“凡此变数中函彼变数者，则此为彼之函数”，即函数指一个量随着另一个量的变化而变化，或者说一个量中含有另一个量。