






湘教版八年级下册4.4 用待定系数法确定一次函数表达式教案配套ppt课件
展开第3课时 一次函数与一次方程的关系
4.5 一次函数的应用
1.通过画及分析一次函数的图象,探究一次函数的图象与一元一次方程的关系,并能利用一次函数的图象求一元一次方程的近似解.2.通过分析同一坐标系内两条直线相交的图形,理解一次函数与二元一次方程组的关系,并能利用此关系解决一些实际问题.
目标一 能利用图象法求一元一次方程的解
例1 教材例3针对训练 直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是x=________.
【归纳总结】一元一次方程ax+b=0的解就是直线y=ax+b与x轴交点的横坐标.
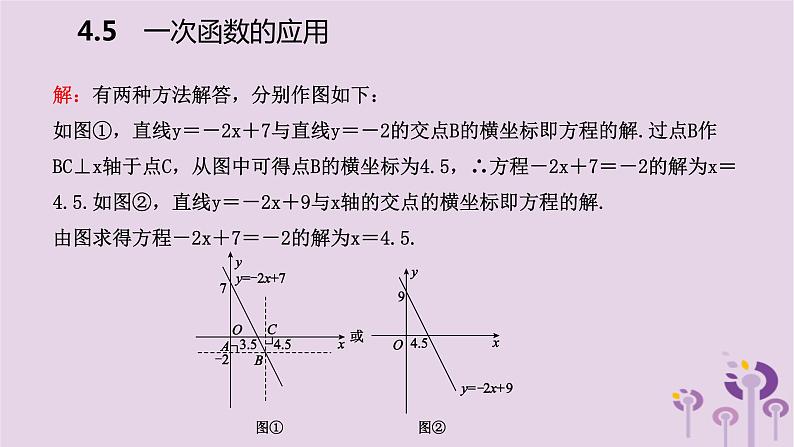
例2 教材补充例题 用图象法求方程-2x+7=-2的解.
[解析] 思路一:作函数y=-2x+7的图象,然后过y轴上表示-2的点A作y轴的垂线,与y=-2x+7的图象交于点B,再过点B作x轴的垂线与x轴交于点C,点C对应的实数即-2x+7=-2的解.思路二:作出函数y=-2x+9的图象,则直线与x轴交点的横坐标即方程-2x+7=-2的解.
解:有两种方法解答,分别作图如下:如图①,直线y=-2x+7与直线y=-2的交点B的横坐标即方程的解.过点B作BC⊥x轴于点C,从图中可得点B的横坐标为4.5,∴方程-2x+7=-2的解为x=4.5.如图②,直线y=-2x+9与x轴的交点的横坐标即方程的解.由图求得方程-2x+7=-2的解为x=4.5.
【归纳总结】对于利用一次函数的图象解ax+b=m类方程,一般有两种思路.思路一:作出函数y=ax+b的图象,再过纵轴上对应m的点作y轴的垂线,与y=ax+b的图象交于一点,再过这一点作x轴的垂线,与x轴交点的横坐标即方程的解;思路二:把m移到方程左边,作出函数y=ax+b-m的图象,与x轴交点的横坐标即方程的解.
目标二 能用两个一次函数图象的交点解决问题
[解析] 首先把方程组中的两个二元一次方程都化为函数的形式,再画出函数图象,从而找出交点坐标.
【归纳总结】两个一次函数图象的交点坐标就是对应的二元一次方程组的解;反之,二元一次方程组的解就是对应的两个一次函数图象的交点坐标.
例4 高频考题 某电信公司给顾客提供了两种手机上网计费方式:方式A,以每分钟0.1元的价格按上网时间计费;方式B,除收月基本费20元外,再以每分钟0.06元的价格按上网时间计费.假设顾客甲一个月手机上网的时间为x(分),上网费用为y(元).
(1)分别写出顾客甲按A,B两种计费方式的上网费y(元)与上网时间x(分)之间的函数表达式,并在图4-5-5所示的直角坐标系中作出这两个函数的图象;(2)如何选择计费方式能使顾客甲的上网费更合算?
【归纳总结】利用一次函数图象求不等式ax+b>0(ax+b<0)解集的步骤(1)作出一次函数的图象;(2)找到图象与x轴的交点;(3)观察图象在x轴上(下)方部分对应的自变量x的取值范围,即是ax+b>0(ax+b<0)的解集.
知识点一 一元一次方程与一次函数的关系
一般地,一次函数y=kx+b(k≠0)的图象与x轴的交点的横坐标是一元一次方程kx+b=0的解.任何一个一元一次方程kx+b=0的解,就是一次函数y=kx+b的图象与x轴交点的______坐标.
知识点二 二元一次方程组与一次函数的关系
一般地,每个二元一次方程组都对应两个一次函数,于是也对应______条直线.从“数”的角度看,解方程组相当于考虑__________为何值时两个函数的值相等,以及这个函数值是何值;从“形”的角度看,解方程组相当于确定两条直线的________坐标.
学完一次函数与一元一次方程的关系后,能不能把一次函数与一元一次不等式联系在一起呢?小明同学遇到了这样的问题:利用函数图象解不等式4x+5
数学4.4 用待定系数法确定一次函数表达式获奖习题课件ppt: 这是一份数学4.4 用待定系数法确定一次函数表达式获奖习题课件ppt,共9页。
初中数学湘教版八年级下册4.4 用待定系数法确定一次函数表达式课文ppt课件: 这是一份初中数学湘教版八年级下册4.4 用待定系数法确定一次函数表达式课文ppt课件,共22页。PPT课件主要包含了逐点学练,本节小结,作业提升,学习目标,本节要点,学习流程,感悟新知,知识点,确定一次函数的表达式,解决实际问题等内容,欢迎下载使用。
湘教版八年级下册4.4 用待定系数法确定一次函数表达式习题ppt课件: 这是一份湘教版八年级下册4.4 用待定系数法确定一次函数表达式习题ppt课件,共31页。













