人教版八年级（上）期中考试数学试卷 解析版

八年级（上）期中数学试卷
一、选择题（共10小题30分）
1．2020年全国上下抗击疫情，众志成城，下列防疫标志图形中是轴对称图形的是（　　）
A． B．
C． D．
2．一个三角形的两边长为2和6，第三边为偶数．则这个三角形的周长为（　　）
A．16 B．14 C．12 D．10
3．如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，若BD＝1，CF＝3，则AB的长是（　　）

A．6 B． C．3 D．4
4．一个n边形的每一个外角都是72°，则n等于（　　）
A．3 B．4 C．5 D．6
5．如图，在平面直角坐标系中，△ABC的顶点都在格点上，如果将△ABC先沿y轴翻折，再向上平移3个单位长度，得到△A'B'C'，那么点B的对应点B'的坐标为（　　）

A．（1，7） B．（0，5） C．（3，4） D．（﹣3，2）
6．如图，在△ABC中，∠ACB＝90°，点D在AB上，将△BDC沿CD折叠，点B落在AC边上的点B′处，若∠ADB′＝20°，则∠A的度数为（　　）

A．20° B．25° C．35° D．40°
7．等腰三角形其中两条边的长度为5和11，则该等腰三角形的周长为（　　）
A．21 B．27 C．21或32 D．21或27
8．如图，在△ABC中，AD⊥BC于点D，BE⊥AC于点E，AD与BE相交于点F，若BF＝AC，∠CAD＝25°，则∠ABE的度数为（　　）

A．30° B．15° C．25° D．20°
9．如图，在△ABC中，DE垂直平分BC，分别交BC、AB于D、E，连接CE，BF平分∠ABC，交CE于F，若BE＝AC，∠ACE＝12°，则∠EFB的度数为（　　）

A．58° B．63° C．67° D．70°
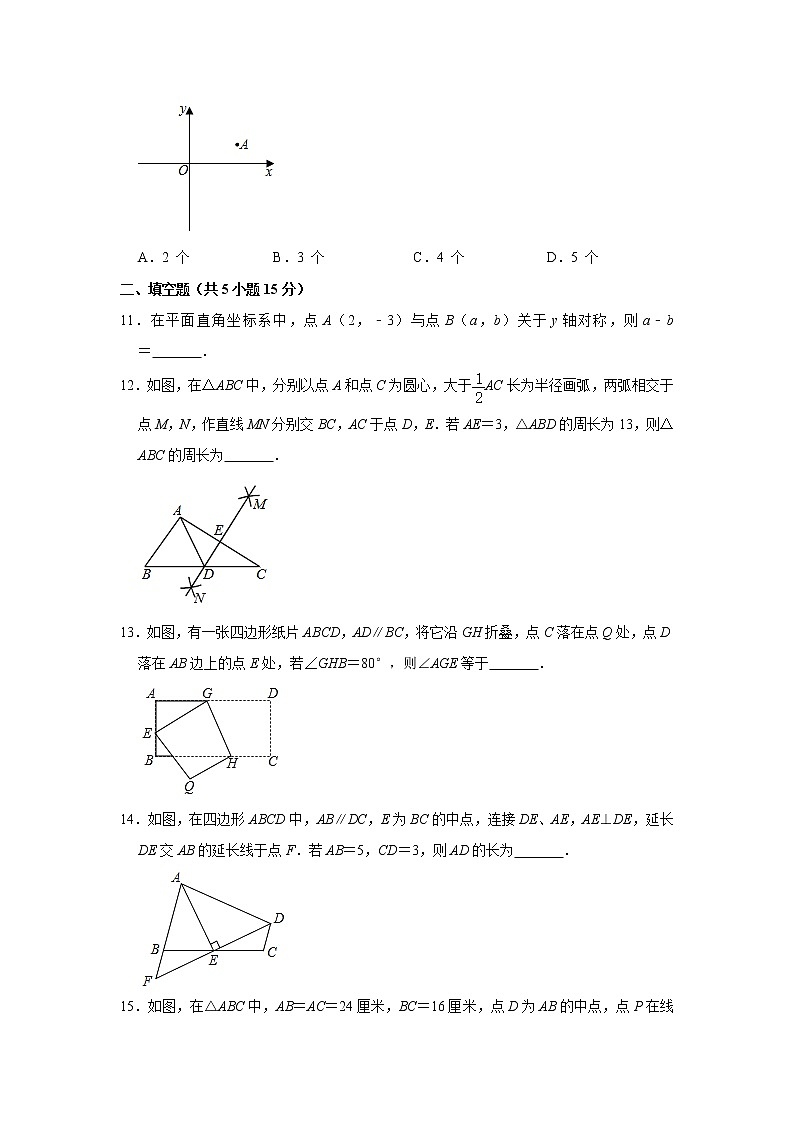
10．如图所示，在平面直角坐标系中，点A（3，1），点P在x轴上，若以P、O、A为顶点的三角形是等腰三角形，则满足条件的点P共有（　　）

A．2 个 B．3 个 C．4 个 D．5 个
二、填空题（共5小题15分）
11．在平面直角坐标系中，点A（2，﹣3）与点B（a，b）关于y轴对称，则a﹣b＝　 　．
12．如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE＝3，△ABD的周长为13，则△ABC的周长为　 　．

13．如图，有一张四边形纸片ABCD，AD∥BC，将它沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠GHB＝80°，则∠AGE等于　 　．

14．如图，在四边形ABCD中，AB∥DC，E为BC的中点，连接DE、AE，AE⊥DE，延长DE交AB的延长线于点F．若AB＝5，CD＝3，则AD的长为　 　．

15．如图，在△ABC中，AB＝AC＝24厘米，BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为　 　厘米/秒时，能够在某一时刻使△BPD与△CQP全等．

三.解答题（共8小题75分）
16．（8分）如图，已知在△ABC中，∠C＝90°，BE平分∠ABC，且BE∥AD，∠BAD＝20°，求∠AEB的度数．

17．（9分）如图，在平面直角坐标系中，每个小正方形的边长均为1，点A的坐标为（﹣2，3），点B的坐标为（﹣3，1），点C的坐标为（1，﹣2）．
（1）作出△ABC关于y轴对称的△A'B'C'（其中A'，B'，C'分别是A，B，C的对应点，不写画法）．
（2）直接写出A'，B'，C'三点的坐标．
（3）在x轴上求作一点P，使PA+PB的值最小．（简要写出作图步骤）

18．（9分）如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1＝46°，求∠BDE的度数．

19．（9分）如图，在△ABC中，∠C＝90°，AB的垂直平分线交AC于点D，垂足为E，若∠A＝30°，CD＝2．
（1）求∠BDC的度数；
（2）求BD的长．

20．（9分）某大学计划为新生配备如图1所示的折叠凳图2是折叠凳撑开后的侧面示意图（木条等材料宽度忽略不计），其中凳腿AB和CD的长相等，O是它们的中点．为了使折叠凳坐着舒适，厂家将撑开后的折叠凳宽度AD设计为30cm，由以上信息能求出CB的长度吗？如果能，请求出BC的长度，如果不能，请你说明理由．

21．（10分）已知，如图，△ABC和△BDE都是等边三角形，且点D在AC上．
（1）求证：△DBC≌△EBA；
（2）直接写出AE，AD和AB之间的关系．

22．（10分）已知：如图，∠XOY＝90°，点A、B分别在射线OX、OY上移动（不与点O重合），BE是∠ABY的平分线，BE的反向延长线与∠OAB的平分线相交于点C．
（1）当∠OAB＝40°时，∠ACB＝　 　度；
（2）随点A、B的移动，试问∠ACB的大小是否变化？如果保持不变，请给出证明；如果发生变化，请求出变化范围．

23．（11分）如图1，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为D，E，AD＝8cm，DE＝5cm．
（1）求BE的长；
（2）其它条件不变的前提下，将CE所在直线旋转到△ABC的外部（如图2），请你猜想AD，DE，BE三者之间的数量关系，直接写出结论，不需证明．
（3）如图3，将（1）中的条件改为：在△ABC中，AC＝BC，D，C，E三点在同一条直线上，并且有∠BEC＝∠ADC＝∠BCA＝α，其中α为任意钝角，那么（2）中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．


2020-2021学年河南省信阳市罗山县八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（共10小题30分）
1．2020年全国上下抗击疫情，众志成城，下列防疫标志图形中是轴对称图形的是（　　）
A． B．
C． D．
【分析】根据轴对称图形的概念：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
【解答】解：A、不是轴对称图形，故此选项不合题意；
B、不是轴对称图形，故此选项不合题意；
C、不是轴对称图形，故此选项不合题意；
D、是轴对称图形，故此选项符合题意；
故选：D．
2．一个三角形的两边长为2和6，第三边为偶数．则这个三角形的周长为（　　）
A．16 B．14 C．12 D．10
【分析】根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边．即可求解．
【解答】解：第三边的取值范围是大于4且小于8，又第三边是偶数，故第三边是6．
则该三角形的周长是14．
故选：B．
3．如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，若BD＝1，CF＝3，则AB的长是（　　）

A．6 B． C．3 D．4
【分析】由“AAS”可证△ADE≌△CFE，可得CF＝AD＝3，即可求解．
【解答】解：∵FC∥AB，
∴∠A＝∠ACF，∠F＝∠ADF，
又∵DE＝EF，
∴△ADE≌△CFE（AAS），
∴CF＝AD＝3，
∴AB＝AD+BD＝4，
故选：D．
4．一个n边形的每一个外角都是72°，则n等于（　　）
A．3 B．4 C．5 D．6
【分析】先判断出此多边形是正多边形，然后根据正多边形的边数等于360°除以每一个外角的度数计算即可得解．
【解答】解：∵多边形的每一个外角都是72°，
∴此多边形是正多边形，
360°÷72°＝5，
所以，它的边数是5．
故选：C．
5．如图，在平面直角坐标系中，△ABC的顶点都在格点上，如果将△ABC先沿y轴翻折，再向上平移3个单位长度，得到△A'B'C'，那么点B的对应点B'的坐标为（　　）

A．（1，7） B．（0，5） C．（3，4） D．（﹣3，2）
【分析】根据轴对称的性质和平移规律求得即可．
【解答】解：由坐标系可得B（﹣3，1），将△ABC先沿y轴翻折得到B点对应点为（3，1），再向上平移3个单位长度，点B的对应点B'的坐标为（3，1+3），
即（3，4），
故选：C．
6．如图，在△ABC中，∠ACB＝90°，点D在AB上，将△BDC沿CD折叠，点B落在AC边上的点B′处，若∠ADB′＝20°，则∠A的度数为（　　）

A．20° B．25° C．35° D．40°
【分析】利用翻折不变性，三角形内角和定理和三角形外角的性质即可解决问题．
【解答】解：∵∠ACB＝90°，
∴∠A+∠B＝90°，
∵△CDB′是由△CDB翻折得到，
∴∠CB′D＝∠B，
∵∠CB′D＝∠A+∠ADB′＝∠A+20°，
∴∠A+∠A+20°＝90°，
解得∠A＝35°．
故选：C．
7．等腰三角形其中两条边的长度为5和11，则该等腰三角形的周长为（　　）
A．21 B．27 C．21或32 D．21或27
【分析】分两种情况讨论，利用等腰三角形的性质可求解．
【解答】解：若5为腰长，则三边为5，5，11，
∵5+5＜11，
∴5，5，11不能构成三角形，
若11为腰长，则三边为5，11，11，
∵5+11＞11，
∴等腰三角形的周长为5+11+11＝27，
故选：B．
8．如图，在△ABC中，AD⊥BC于点D，BE⊥AC于点E，AD与BE相交于点F，若BF＝AC，∠CAD＝25°，则∠ABE的度数为（　　）

A．30° B．15° C．25° D．20°
【分析】利用全等三角形的性质即可解决问题；
【解答】解：∵AD⊥BC，
∴∠BDF＝∠ADC，
又∵∠BFD＝∠AFE，
∴∠CAD＝∠FBD，
在△BDF和△ADC中
，
∴△BDF≌△ADC （AAS）
∴∠DBF＝∠CAD＝25°，
∵DB＝DA，∠ADB＝90°，
∴∠ABD＝45°，
∴∠ABE＝∠ABD﹣∠DBF＝20°
故选：D．
9．如图，在△ABC中，DE垂直平分BC，分别交BC、AB于D、E，连接CE，BF平分∠ABC，交CE于F，若BE＝AC，∠ACE＝12°，则∠EFB的度数为（　　）

A．58° B．63° C．67° D．70°
【分析】根据线段垂直平分线上的性质得到EB＝EC，根据等腰三角形的性质得到∠EBC＝∠ECB，根据三角形内角和定理、三角形的外角性质计算，得到答案．
【解答】解：∵DE垂直平分BC，
∴EB＝EC，
∴∠EBC＝∠ECB，
∵EB＝EC，BE＝AC，
∴AC＝EC，
∴∠AEC＝∠EAC＝×（180°﹣12°）＝84°，
∴∠EBC＝∠ECB＝∠AEC＝42°，
∵BF平分∠ABC，
∴∠EBF＝∠CBF＝21°，
∴∠EFB＝∠AEC﹣∠EBF＝63°，
故选：B．
10．如图所示，在平面直角坐标系中，点A（3，1），点P在x轴上，若以P、O、A为顶点的三角形是等腰三角形，则满足条件的点P共有（　　）

A．2 个 B．3 个 C．4 个 D．5 个
【分析】分别以点O、A为圆心，以OA的长度为半径画弧，与x轴的交点即为所求的点P的位置．
【解答】解：如图，以点O、A为圆心，以OA的长度为半径画弧，OA的垂直平分线与x轴的交点有4个．
故选：C．

二、填空题（共5小题15分）
11．在平面直角坐标系中，点A（2，﹣3）与点B（a，b）关于y轴对称，则a﹣b＝　1　．
【分析】根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”求出a、b的值，然后代入计算即可得解．
【解答】解：∵点A（2，﹣3）与点B（a，b）关于y轴对称，
∴a＝﹣2，b＝﹣3，
∴a﹣b＝﹣2+3＝1．
故答案为：1．
12．如图，在△ABC中，分别以点A和点C为圆心，大于AC长为半径画弧，两弧相交于点M，N，作直线MN分别交BC，AC于点D，E．若AE＝3，△ABD的周长为13，则△ABC的周长为　19　．

【分析】利用线段的垂直平分线的性质即可解决问题．
【解答】解：∵DE垂直平分线段AC，
∴DA＝DC，AE+EC＝6，
∵AB+AD+BD＝13，
∴AB+BD+DC＝13，
∴△ABC的周长＝AB+BD+BC+AC＝13+6＝19，
故答案为：19．
13．如图，有一张四边形纸片ABCD，AD∥BC，将它沿GH折叠，点C落在点Q处，点D落在AB边上的点E处，若∠GHB＝80°，则∠AGE等于　20°　．

【分析】根据平行线的性质可得∠DGH＝∠GHB＝80°，再根据折叠的性质可得∠EGH＝∠DGH＝80°，然后根据平角的定义求解即可．
【解答】解：∵AD∥BC，
∴∠DGH＝∠GHB＝80°，
由折叠的性质可得∠EGH＝∠DGH＝80°，
∴∠AGE＝180°﹣∠EGH﹣∠DGH＝180°﹣80°﹣80°＝20°．
故答案为：20°．
14．如图，在四边形ABCD中，AB∥DC，E为BC的中点，连接DE、AE，AE⊥DE，延长DE交AB的延长线于点F．若AB＝5，CD＝3，则AD的长为　8　．

【分析】由“AAS”可证△BEF≌△CED，可得EF＝DE，BF＝CD＝3，由线段垂直平分线的性质可得AD＝AF＝8．
【解答】解：∵E为BC的中点，
∴BE＝EC，
∵AB∥CD，
∴∠F＝∠CDE，且∠BEF＝∠CED，BE＝EC，
∴△BEF≌△CED（AAS）
∴EF＝DE，BF＝CD＝3，
∴AF＝AB+BF＝8，
∵AE⊥DE，EF＝DE，
∴AF＝AD＝8．
15．如图，在△ABC中，AB＝AC＝24厘米，BC＝16厘米，点D为AB的中点，点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．当点Q的运动速度为　4或6　厘米/秒时，能够在某一时刻使△BPD与△CQP全等．

【分析】首先求出BD的长，要使△BPD与△CQP全等，必须BD＝CP或BP＝CP，得出方程12＝16﹣4x或4x＝16﹣4x，求出方程的解即可．
【解答】解：设经过x秒后，使△BPD与△CQP全等，
∵AB＝AC＝24厘米，点D为AB的中点，
∴BD＝12厘米，
∵∠ABC＝∠ACB，
∴要使△BPD与△CQP全等，必须BD＝CP或BP＝CP，
即12＝16﹣4x或4x＝16﹣4x，
解得：x＝1或x＝2，
x＝1时，BP＝CQ＝4，4÷1＝4；
x＝2时，BD＝CQ＝12，12÷2＝6；
即点Q的运动速度是4或6，
故答案为：4或6
三.解答题（共8小题75分）
16．（8分）如图，已知在△ABC中，∠C＝90°，BE平分∠ABC，且BE∥AD，∠BAD＝20°，求∠AEB的度数．

【分析】根据平行线的性质和三角形外角的性质即可得到结论．
【解答】解：∵BE∥AD，
∴∠ABE＝∠BAD＝20°，
∵BE平分∠ABC，
∴∠EBC＝∠ABE＝20°，
∵∠C＝90°，
∴∠AEB＝∠C+∠CBE＝90°+20°＝110°．
17．（9分）如图，在平面直角坐标系中，每个小正方形的边长均为1，点A的坐标为（﹣2，3），点B的坐标为（﹣3，1），点C的坐标为（1，﹣2）．
（1）作出△ABC关于y轴对称的△A'B'C'（其中A'，B'，C'分别是A，B，C的对应点，不写画法）．
（2）直接写出A'，B'，C'三点的坐标．
（3）在x轴上求作一点P，使PA+PB的值最小．（简要写出作图步骤）

【分析】（1）分别作出三个顶点关于x轴的对称点，再首尾顺次连接即可得；
（2）根据所作图形可得各顶点坐标；
（3）找到点B关于x轴的对称点B''，连接AB''交x轴于点P，连接PB，此时PA+PB的值最小．
【解答】解：（1）如图所示，△A'B'C'即为所求；


（2）A'（2，3），B'（3，1），C'（﹣1，﹣2）；

（3）如图所示，P点即为所求．
18．（9分）如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1＝46°，求∠BDE的度数．

【分析】（1）根据全等三角形的判定即可判断△AEC≌△BED；
（2）由（1）可知：EC＝ED，∠C＝∠BDE，根据等腰三角形的性质即可知∠C的度数，从而可求出∠BDE的度数；
【解答】解：（1）证明：∵AE和BD相交于点O，
∴∠AOD＝∠BOE．
在△AOD和△BOE中，∠A＝∠B，
∴∠BEO＝∠2．
又∵∠1＝∠2，
∴∠1＝∠BEO，
∴∠AEC＝∠BED．
在△AEC和△BED中，
，
∴△AEC≌△BED（ASA）．
（2）∵△AEC≌△BED
∴DE＝CE
∴∠EDC＝∠C
∵∠1＝46°
∴∠EDC＝∠C＝67°
∵△AEC≌△BED
∴∠BDE＝∠C＝67°
19．（9分）如图，在△ABC中，∠C＝90°，AB的垂直平分线交AC于点D，垂足为E，若∠A＝30°，CD＝2．
（1）求∠BDC的度数；
（2）求BD的长．

【分析】（1）由于AB的垂直平分线交AC于点D，根据线段的垂直平方的性质得到DA＝DB，然后根据等腰三角形的性质推出∠DBE＝∠A，然后利用已知条件即可求出∠BDC的度数；
（2）利用已知条件和30°的角所对的直角边等于斜边的一半即可求出BD的长．
【解答】解：（1）∵DE垂直平分AB，
∴DA＝DB，
∴∠DBE＝∠A＝30°，
∴∠BDC＝60°；
（2）在Rt△BDC中，∵∠BDC＝60°，
∴∠DBC＝30°，
∴BD＝2CD＝4．
20．（9分）某大学计划为新生配备如图1所示的折叠凳图2是折叠凳撑开后的侧面示意图（木条等材料宽度忽略不计），其中凳腿AB和CD的长相等，O是它们的中点．为了使折叠凳坐着舒适，厂家将撑开后的折叠凳宽度AD设计为30cm，由以上信息能求出CB的长度吗？如果能，请求出BC的长度，如果不能，请你说明理由．

【分析】根据中点定义求出OA＝OB，OC＝OD，然后利用“边角边”证明△AOD和△BOC全等，根据全等三角形对应边相等即可证明．
【解答】解：∵O是AB、CD的中点，
∴OA＝OB，OC＝OD，
在△AOD和△BOC中，，
∴△AOD≌△BOC（SAS），
∴CB＝AD，
∵AD＝30cm，
∴CB＝30cm．
21．（10分）已知，如图，△ABC和△BDE都是等边三角形，且点D在AC上．
（1）求证：△DBC≌△EBA；
（2）直接写出AE，AD和AB之间的关系．

【分析】（1）由“SAS”可证△DBC≌△EBA；
（2）由全等三角形的性质可求解．
【解答】（1）证明：∵△ABC和△BDE都是等边三角形，
∴AB＝BC，BE＝BD，∠ABC＝∠DBE＝∠C＝60°，
∴∠ABC﹣∠ABD＝∠DBE﹣∠ABD，
∴∠DBC＝∠EBA，
在△DBC和△EBA中，
，
∴△DBC≌△EBA（SAS）；
∴∠C＝∠EAB＝∠ABC，
∴EA∥BC
（2）解：AE+AD＝AB，理由如下：
∵△DBC≌△EBA，
∴AE＝CD，
∵AD+CD＝AC＝AB，
∴AE+AD＝AB．
22．（10分）已知：如图，∠XOY＝90°，点A、B分别在射线OX、OY上移动（不与点O重合），BE是∠ABY的平分线，BE的反向延长线与∠OAB的平分线相交于点C．
（1）当∠OAB＝40°时，∠ACB＝　45　度；
（2）随点A、B的移动，试问∠ACB的大小是否变化？如果保持不变，请给出证明；如果发生变化，请求出变化范围．

【分析】（1）先利用角平分线得出∠CAB＝∠OAB，∠EBA＝∠YBA，再利用三角形的外角的性质即可得出结论；
（2）先利用角平分线得出∠CAB＝∠OAB，∠EBA＝∠YBA，再利用三角形的外角的性质即可得出结论．
【解答】解：（1）∵∠XOY＝90°，∠OAB＝40°，
∴∠ABY＝130°，
∵AC平分∠OAB，BE平分∠YBA，
∴∠CAB＝∠OAB＝20°，∠EBA＝∠YBA＝65°，
∵∠EBA＝∠C+∠CAB，
∴∠C＝∠EBA﹣∠CAB＝45°，
故答案为：45；
（2）∠ACB的大小不变化．
理由：∵AC平分∠OAB，BE平分∠YBA，
∴∠CAB＝∠OAB，∠EBA＝∠YBA，
∵∠EBA＝∠C+∠CAB，
∴∠C＝∠EBA﹣∠CAB＝∠YBA﹣∠OAB＝（∠YBA﹣∠OAB），
∵∠YBA﹣∠OAB＝90°，
∴∠C＝×90°＝45°，
即：∠ACB的大小不发生变化．
23．（11分）如图1，∠ACB＝90°，AC＝BC，AD⊥CE，BE⊥CE，垂足分别为D，E，AD＝8cm，DE＝5cm．
（1）求BE的长；
（2）其它条件不变的前提下，将CE所在直线旋转到△ABC的外部（如图2），请你猜想AD，DE，BE三者之间的数量关系，直接写出结论，不需证明．
（3）如图3，将（1）中的条件改为：在△ABC中，AC＝BC，D，C，E三点在同一条直线上，并且有∠BEC＝∠ADC＝∠BCA＝α，其中α为任意钝角，那么（2）中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．

【分析】（1）先利用同角的余角相等判断出∠EBC＝∠DCA，进而判断出△CEB≌△ADC，得出BE＝DC，CE＝AD＝8cm，即可得出结论；
（2）同（1）的方法得出BE＝DC，CE＝AD，进而得出结论．
（3）同（1）的方法，即可得出结论．
【解答】解：（1）∵BE⊥CE，AD⊥CE，
∴∠E＝∠ADC＝90°，
∴∠EBC+∠BCE＝90°．
∵∠BCE+∠ACD＝90°，
∴∠EBC＝∠DCA．
在△CEB和△ADC中，
，
∴△CEB≌△ADC（AAS），
∴BE＝DC，CE＝AD＝8cm．
∵DC＝CE﹣DE，DE＝5cm，
∴DC＝8﹣5＝3（cm），
∴BE＝3cm；

（2）AD+BE＝DE，
证明：∵BE⊥CE，AD⊥CE，
∴∠E＝∠ADC＝90°，
∴∠EBC+∠BCE＝90°，
∵∠BCE+∠ACD＝90°，
∴∠EBC＝∠DCA．
在△CEB和△ADC中，
，
∴△CEB≌△ADC（AAS），
∴BE＝DC，CE＝AD，
∴DE＝CE+DE＝AD+BE；

（3）、（2）中的猜想还成立，
证明：∵∠BCE+∠ACB+∠ACD＝180°，∠DAC+∠ACB+∠ACD＝180°，∠ADC＝∠BCA，
∴∠BCE＝∠CAD，
在△CEB和△ADC中，
，
∴△CEB≌△ADC（AAS），
∴BE＝CD，EC＝AD，
∴DE＝EC+CD＝AD+BE．