初中数学24.4 弧长及扇形的面积教案及反思

这是一份初中数学24.4 弧长及扇形的面积教案及反思，共4页。教案主要包含了导入，知识讲解，应用举例，难点突破，课堂练习，难点巩固等内容，欢迎下载使用。
教师姓名
单位名称
填写时间
2020年8月12日
学科
数学
年级/册
九年级（上）
教材版本
人教版
课题名称



微课----巧用等积法解题



难点名称
熟练运用等积法解实际问题。
难点分析
从知识角度分析为什么难



等积法两种含义的理解较为复杂抽象，容易混淆，因此具有一定的难度。将直观想象数学核心素养在解题过程中得以体现，也是有一定难度的。
从学生角度分析为什么难
学生对等积法运用直观想象来解决问题，感到很陌生，还不习惯于用这一方法来高效、简捷的解决问题。解题过程中往往想不起用这种方法解题。也没有分清楚什么情况下用等积法解题。
难点教学方法



1、通过教师对等积法的内涵和外延的解释，教会学生使用分析运用等积法的条件，加深学生对转化思想的认识，强化学生的应用能力。


2、通过问题的分析、过程演示、思路讲解，引领学生发现等积法的本质，体会运用等积法在解决一些数学问题中体现出的方便快捷，展现数学方法之精妙，应用之广泛，培养学生学习数学的热情。
教学环节
教学过程
设计意图
导入
一、导入：


等积法：利用不同的方法表示同一个平面图形的面积，计算结果始终相等，利用这一原理证明或计算某些数学问题的数学方法称为等积法。



让学生理解等积法的概念。然后教师提问：怎么理解呢？


引发学生的思考，将注意力集中到课堂上来。
知识讲解


（难点突破）
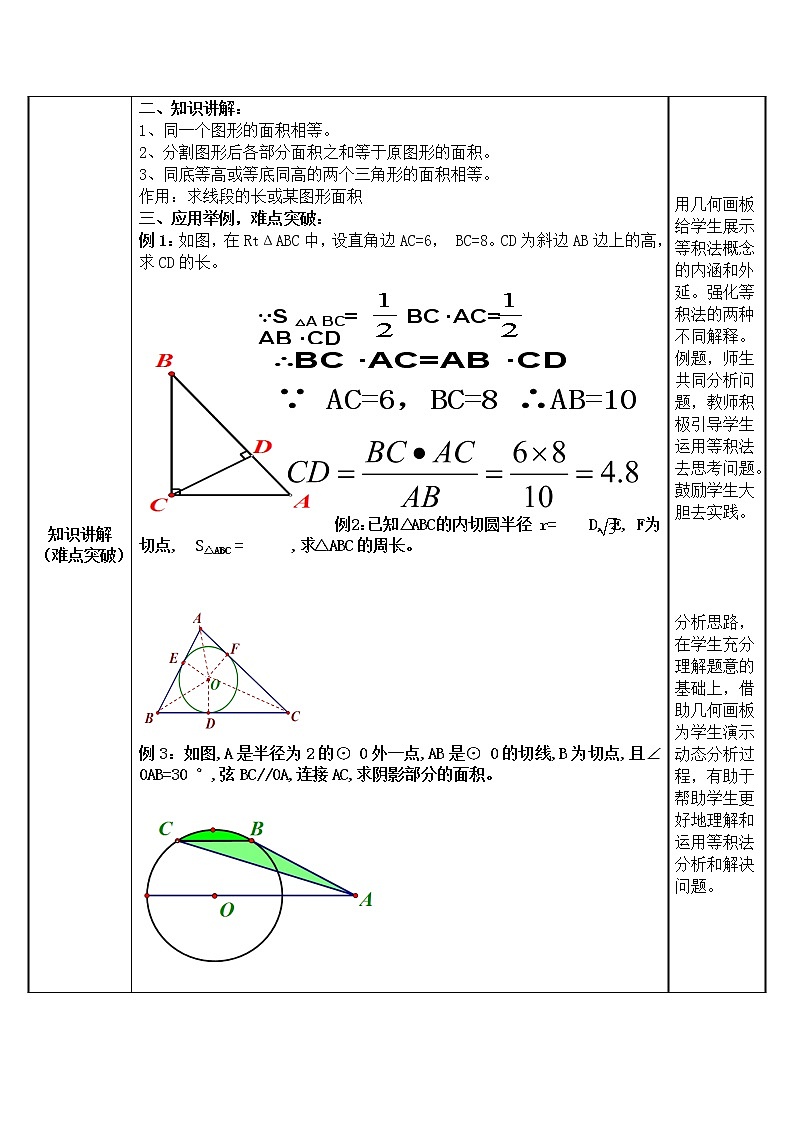
二、知识讲解：


1、同一个图形的面积相等。


2、分割图形后各部分面积之和等于原图形的面积。


3、同底等高或等底同高的两个三角形的面积相等。


作用：求线段的长或某图形面积


三、应用举例，难点突破：


例1：如图，在RtΔABC中，设直角边AC=6， BC=8。CD为斜边AB边上的高，求CD的长。


























例2： 已知△ABC的内切圆半径 r= D, E, F为切点, S△ABC = ,求△ABC的周长。











例3：如图,A是半径为2的⊙ 0外一点,AB是⊙ 0的切线,B为切点,且∠ 0AB=30 °,弦BC//0A,连接AC,求阴影部分的面积。









用几何画板给学生展示等积法概念的内涵和外延。强化等积法的两种不同解释。


例题，师生共同分析问题，教师积极引导学生运用等积法去思考问题。鼓励学生大胆去实践。














分析思路，在学生充分理解题意的基础上，借助几何画板为学生演示动态分析过程，有助于帮助学生更好地理解和运用等积法分析和解决问题。
课堂练习


（难点巩固）
四、课堂练习，难点巩固：


1、已知：如图，菱形ABCD中两对角线AC、BD分别长10和24，BC边上的高是h，求h的值？





2、如图，矩形ABCD中，AC、BD交于O点，BE⊥AC于E，CF⊥BD于F，


求证：BE=CF





3、 [2019.南充中考]如图,在半径为6的⊙ 0中,点A,B,C都在⊙ 0上,四边形0ABC是平行四边形,则图中阴影部分的面积为( )

















4、如图,在△ ABC中,AB=AC,P为t算方 BC上一点,PE ⊥ AB于E,PF ⊥ AC于F,求证:PE+ PF为定值。





5、已知：如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点(点P不与点A、C重合)，且PE//BC交AB于E，PF//CD交AD于F，则阴影部分的面积是（ ）



课堂练习，旨在为学生训练等积法的使用方法和技巧，因此教师不必讲太多只是点拨即可。主要是让学生体会到用等积法解决实际问题的好处。使学生明白当解题过程中如果思维受阻时我们可以用等积法来解决问题。
小结