2021版新高考数学（山东专用）一轮学案：第一章第二讲　命题及其关系、充分条件与必要条件


第二讲　命题及其关系、充分条件与必要条件

ZHI SHI SHU LI SHUANG JI ZI CE
知识梳理·双基自测

知识点一　命题及四种命题之间的关系
1．命题
用语言、符号或式子表达的，可以判断真假的陈述句叫做命题，其中判断为真的语句叫做真命题，判断为假的语句叫做假命题．
2．四种命题及其关系
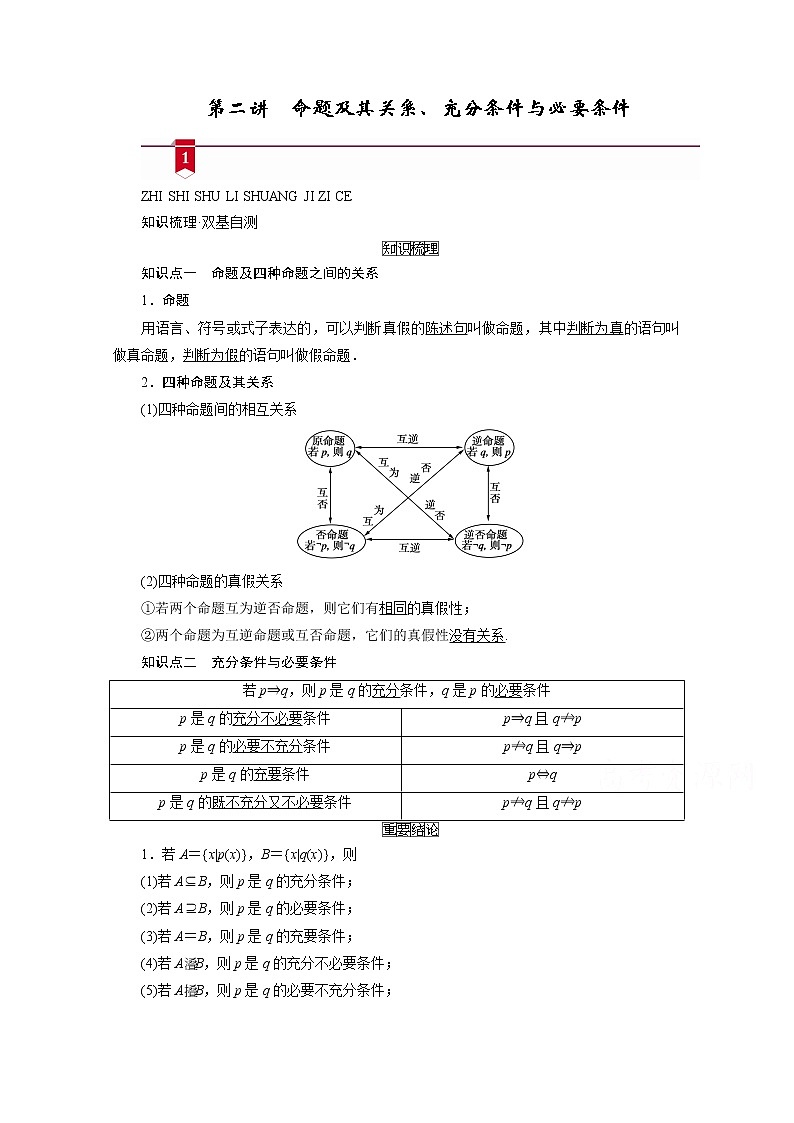
(1)四种命题间的相互关系

(2)四种命题的真假关系
①若两个命题互为逆否命题，则它们有相同的真假性；
②两个命题为互逆命题或互否命题，它们的真假性没有关系.
知识点二　充分条件与必要条件
若p⇒q，则p是q的充分条件，q是p的必要条件
p是q的充分不必要条件
p⇒q且qp
p是q的必要不充分条件
pq且q⇒p
p是q的充要条件
p⇔q
p是q的既不充分又不必要条件
pq且qp

1．若A＝{x|p(x)}，B＝{x|q(x)}，则
(1)若A⊆B，则p是q的充分条件；
(2)若A⊇B，则p是q的必要条件；
(3)若A＝B，则p是q的充要条件；
(4)若AB，则p是q的充分不必要条件；
(5)若AB，则p是q的必要不充分条件；
(6)若AB且A⊉B，则p是q的既不充分也不必要条件．
2．充分条件与必要条件的两个特征：
(1)对称性：若p是q的充分条件，则q是p的必要条件，即“p⇒q”⇔“q⇐p”．
(2)传递性：若p是q的充分(必要)条件，q是r的充分(必要)条件，则p是r的充分(必要)条件，即“p⇒q且q⇒r”⇒“p⇒r”(“p⇐q且q⇐r”⇒“p⇐r”)．
注意：不能将“若p，则q”与“p⇒q”混为一谈，只有“若p，则q”为真命题时，才有“p⇒q”，即“p⇒q”⇔“若p，则q”为真命题．

　　　　　　　　　　　　　　　　　　　　　


题组一　走出误区
1．(多选题)下列命题正确的是(　BD　)
A．命题“三角形的内角和是180°”的否命题是“三角形的内角和不是180°”
B．已知集合A，B，则A∪B＝A∩B的充要条件是A＝B
C．“α＝β”是“tan α＝tan β”的充分不必要条件
D．“若p不成立，则q不成立”等价于“若q成立，则p成立”
[解析]　A不正确，B、D正确；对于C，当α＝β＝时，tan α、tan β都无意义．因此不能设tan α＝tan β，当tan α＝tan β时，α＝β＋kπ，k∈Z，不一定α＝β，因此是既不充分也不必要条件．故选B、D．
题组二　走进教材
2．(选修2－1P8T3改编)下列命题是真命题的是(　A　)
A．矩形的对角线相等
B．若a>b，c>d，则ac>bd
C．若整数a是素数，则a是奇数
D．命题“若x2>0，则x>1”的逆否命题
3．(选修2－1P10T4改编)x2－3x＋2≠0是x≠1的充分不必要条件．
[解析]　x＝1是x2－3x＋2＝0的充分不必要条件．
题组三　考题再现
4．(2019·天津，5分)设x∈R，则“x2－5x<0”是“|x－1|<1”的(　B　)
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分也不必要条件
[解析]　由x2－5x<0可得0 5．(2015·山东，5分)设m∈R，命题“若m>0，则方程x2＋x－m＝0有实根”的逆否命题是(　D　)
A．若方程x2＋x－m＝0有实根，则m>0
B．若方程x2＋x－m＝0有实根，则m≤0
C．若方程x2＋x－m＝0没有实根，则m>0
D．若方程x2＋x－m＝0没有实根，则m≤0
[解析]　由原命题和逆否命题的关系可知D正确．
6．(2018·北京，5分)能说明“若f(x)>f(0)对任意的x∈(0,2]都成立，则f(x)在[0,2]上是增函数”为假命题的一个函数是f(x)＝sin_x(答案不唯一).
[解析]　这是一道开放性试题，答案不唯一，只要满足f(x)>f(0)对任意的x∈(0,2]都成立，且函数f(x)在[0,2]上不是增函数即可．如f(x)＝sin x，答案不唯一．


KAO DIAN TU PO HU DONG TAN JIU
考点突破·互动探究
考点一　命题及其关系——自主练透
例1 (1)命题“若a>b，则a2>b2”，能说明该命题为假命题的一组a，b的值依次为1，－2(不唯一).若此命题正确应增加的条件为a>b>0(不唯一).
(2)(多选题)下列命题正确的是(　AC　)
A．“若x＋y＝0，则x、y互为相反数”的逆命题
B．“全等三角形面积相等”的否命题
C．“若q≤－1，则x2＋x＋q＝0有实数根”的逆否命题
D．若ab是正整数，则a、b都是正整数
(3)(2020·长春模拟)已知命题α：如果x<3，那么x<5，命题β：如果x≥3，那么x≥5，则命题α是命题β的(　A　)
A．否命题 B．逆命题
C．逆否命题 D．否定形式
(4)命题“若a＋b＝0，则a，b中最多有一个大于零”的否定形式为若a＋b＝0，则a，b都大于零，否命题为若a＋b≠0，则a，b都大于零.
[解析]　(1)代入特殊值，当a＝1，b＝－2，发现a2b>0时可得a2>b2.
(2)A．“若x＋y＝0，则x、y互为相反数”的逆命题为“若x、y互为相反数，则x＋y＝0”，显然是真命题；B．“全等三角形面积相等”的否命题为“不全等三角形的面积不相等”，假命题；C．“若q≤－1，则x2＋x＋q＝0有实根”的逆否命题为“若x2＋x＋q＝0无实根，则q>－1”，x2＋x＋q＝0无实根则Δ＝1－4q<0，即q>，从而q>－1，故C为真命题．(也可由原命题为真得出结论)；D．显然是假命题，如ab＝2时，可能a＝－1，b＝－2，故填A、C．
(3)命题α：如果x<3，那么x<5，
命题β：如果x≥3，那么x≥5，
则命题α是命题β的否命题．
(4)否定形式：若a＋b＝0，则a，b都大于零．否命题：若a＋b≠0，则a，b都大于零．

名师点拨 ☞
(1)由原命题写出其他三种命题，关键要分清原命题的条件和结论，如果命题不是“若p，则q”的形式，应先改写成“若p，则q”的形式；如果命题有大前提，写其他三种命题时需保留大前提不变．
(2)判断一个命题为真命题，要给出严格的推理证明；判断一个命题为假命题，只需举出反例．
(3)根据“原命题与逆否命题同真同假，逆命题与否命题同真同假”这一性质，当一个命题直接判断不易进行时，可转化为判断其等价命题的真假．
考点二　充分必要条件
考向1　充分条件与必要条件的判断——师生共研
方法1：定义法判断
例2 (2019·浙江，4分)设a>0，b>0，则“a＋b≤4”是“ab≤4”的(　A　)
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
[解析]　方法一：因为a>0，b>0，所以a＋b≥2，由a＋b≤4可得2≤4，解得ab≤4，所以充分性成立；当ab≤4时，取a＝8，b＝，满足ab≤4，但a＋b>4，所以必要性不成立．所以“a＋b≤4”是“ab≤4”的充分不必要条件．故选A．
方法二：在同一坐标系内作出函数b＝4－a，b＝的图象，如图，则不等式a＋b≤4与ab≤4表示的平面区域分别是直线a＋b＝4及其左下方(第一象限中的部分)与曲线b＝及其左下方(第一象限中的部分)，易知当a＋b≤4成立时，ab≤4成立，而当ab≤4成立时，a＋b≤4不一定成立．故选A．

方法2：集合法判断
例3 (2018·天津，4)设x∈R，则“|x－|<”是“x3<1”的(　A　)
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分也不必要条件
[解析]　本题主要考查解不等式和充分、必要条件的判断．
由|x－|<得－ 由x3<1得x<1.因为(0,1)(－∞，1)，所以“|x－|<”是“x3<1”的充分而不必要条件．
方法3　等价转化法判断
例4 (1)给定两个条件p，q，若¬p是q的必要不充分条件，则p是¬q的(　A　)
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
(2)“已知命题p：cosα≠，命题q：α≠”，则命题p是命题q的(　A　)
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
[解析]　(1)因为¬p是q的必要不充分条件，则q⇒¬p，但¬pq，其逆否命题为p⇒¬q，但¬qp，所以p是¬q的充分不必要条件．
(2) ¬p：cosα＝，¬q：α＝，显然¬q⇒¬p，¬p¬q，∴¬q是¬p的充分不必要条件，从而p是q的充分不必要条件，故选A．
另解：若cosα≠，则α≠2kπ±(k∈Z)，则α也必然不等于，故p⇒q；若α≠，但α＝－时，依然有cosα＝，故qp.所以p是q的充分不必要条件．故选A．


名师点拨 ☞
有关充要条件的判断常用的方法
(1)根据定义判断：①弄清条件p和结论q分别是什么；②尝试p⇒q，q⇒p.若p⇒q，则p是q的充分条件；若q⇒p，则p是q的必要条件；若p⇒q，qp，则p是q的充分不必要条件；若pq，q⇒p，则p是q的必要不充分条件；若p⇒q，q⇒p，则p是q的充要条件．
(2)利用集合判断
记法
A＝{x|p(x)}，B＝{x|q(x)}
关系
AB
BA
A＝B
AB且BA
结论
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分也不必要条件
(3)利用等价转化法：对于带有否定性词语的命题，常用此法，即要判断p是q的什么条件，只需判断¬q是¬p的什么条件．
〔变式训练1〕
(1)指出下列各组中，p是q的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选出一种作答)．
①在△ABC中，p：A＝B，q：sinA＝sinB；
②已知x，y∈R，p：(x－1)2＋(y－2)2＝0，q：(x－1)(y－2)＝0；
③非空集合A，B中，p：x∈(A∪B)，q：x∈B；
④对于实数x，y，p：x＋y≠8，q：x≠2或y≠6.
(2)(2019·北京，5分)设函数f(x)＝cos x＋bsin x(b为常数)，则“b＝0”是“f(x)为偶函数”的(　C　)
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
[解析]　(1)①在△ABC中，A＝B⇒sinA＝sinB；反之，若sinA＝sinB，因为A与B不可能互补(三角形三个内角之和为180°)，所以只有A＝B，故p是q的充要条件．
②条件p：x＝1且y＝2，条件q：x＝1或y＝2，所以p⇒q但qp，故p是q的充分不必要条件．
③显然x∈(A∪B)不一定有x∈B，但x∈B一定有x∈(A∪B)，所以p是q的必要不充分条件．
④易知¬p：x＋y＝8，¬q：x＝2且y＝6，显然¬q⇒¬p，但¬p¬q，但¬q是¬p的充分不必要条件，根据原命题和逆否命题的等价性知，p是q的充分不必要条件．
(2)b＝0时，f(x)＝cos x，显然f(x)是偶函数，故“b＝0”是“f(x)是偶函数”的充分条件；f(x)是偶函数，则有f(－x)＝f(x)，即cos(－x)＋bsin(－x)＝cos x＋bsin x，又cos(－x)＝cos x，sin(－x)＝－sin x，所以cos x－bsin x＝cos x＋bsin x，则2bsin x＝0对任意x∈R恒成立，得b＝0，因此“b＝0”是“f(x)是偶函数”的必要条件．因此“b＝0”是“f(x)是偶函数”的充分必要条件，故选C．
考向2　充要条件的应用——多维探究
角度1　充要条件的探究
例5 (多选题)(2020·江西赣州十四县市高三上期中改编)角A，B是△ABC的两个内角．下列六个条件下，“A>B”的充要条件是(　ABD　)
A．sin A>sin B B．cos A C．tan A>tan B D．cos2A [解析]　当A>B时，根据“大边对大角”可知，a>b，由于＝，所以sin A>sin B，则A是“A>B”的充要条件；由于0B”的充要条件；当A>B时，若A为钝角，B为锐角，则tan A<0B”的充要条件；当cos2Asin2B，所以D是“A>B”的充要条件；故选A、B、D．
角度2　利用充要条件求参数的值或取值范围
例6 (2020·山东省实验中学高三诊断)已知p：x≥k，q：(x＋1)(2－x)<0.如果p是q的充分不必要条件，那么实数k的取值范围是(　B　)
A．[2，＋∞) B．(2，＋∞)
C．[1，＋∞) D．(－∞，－1]
[解析]　由q：(x＋1)(2－x)<0，可知q：x<－1或x>2.因为p是q的充分不必要条件，所以x≥k⇒x<－1或x>2，即[k，＋∞)是(－∞，－1)∪(2，＋∞)的真子集，故k>2.故选B．

名师点拨 ☞
充分条件、必要条件的应用，一般表现在参数问题的求解上．解题时需注意：
(1)把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解．
(2)一定要注意端点值的取舍，处理不当容易出现漏解或增解的现象．
(3)注意区别以下两种不同说法：①p是q的充分不必要条件，是指p⇒q但qp；②p的充分不必要条件是q，是指q⇒p但pq.
(4)注意下列条件的等价转化：①p是q的什么条件等价于¬q是¬p的什么条件，②p是¬q的什么条件等价于q是¬p的什么条件．
〔变式训练2〕
(1)(角度1)(2020·陕西西安长安一中第二次月考)命题“对任意x∈[1,2]，x2－a≤0”为真命题的一个充分不必要条件可以是(　B　)
A．a≥4 B．a>4
C．a≥1 D．a>1
(2)(角度2)(2020·福建三明月考)设命题p：|4x－3|≤1，q：x2－(2a＋1)x＋a(a＋1)≤0，若¬p是¬q的必要不充分条件，则实数a的取值范围是(　A　)
A．[0，] B．(0，)
C．(－∞，0]∪[，＋∞) D．(－∞，0)∪(，＋∞)
[解析]　(1)要使“对任意x∈[1,2]，x2－a≤0”为真命题，只需a≥4，∴a>4是命题为真命题的充分不必要条件．故选B．
(2)由|4x－3|≤1得≤x≤1，由x2－(2a＋1)x＋a(a＋1)＝(x－a)[x－(a＋1)]≤0得a≤x≤a＋1，
因为¬p是¬q的必要不充分条件，
所以p是q的充分不必要条件，有得0≤a≤.故选A．


MING SHI JIANG TAN SU YANG TI SHENG
名师讲坛┃·素养提升
抽象命题间充要条件的判定
例7 已知p是r的充分不必要条件，q是r的充分条件，s是r的必要条件，q是s的必要条件，现有下列命题：①r是q的充要条件；②p是q的充分不必要条件；③r是q的必要不充分条件；④¬p是¬s的必要不充分条件；⑤r是s的充分不必要条件，则正确命题的序号是(　B　)
A．①④⑤ B．①②④
C．②③⑤ D．②④⑤
[分析]　本题涉及命题较多，关系复杂，因此采用“图解法”．
[解析]　由题意得p，显然q⇒r且r⇒s⇒q，即q⇔r，①正确；p⇒r⇒s⇒q且qp，②正确；r⇔q，③错误；由p⇒s知¬s⇒¬p，但sp，∴¬p¬s，④正确；r⇔s，⑤错误．故选B．

名师点拨 ☞
命题较多、关系复杂时，画出各命题间关系图求解，简洁直观，一目了然．
〔变式训练3〕
　若p是r的必要不充分条件，q是r的充分条件，则p是q的必要不充分条件．
[解析]　由题意可知q⇒rp，∴p是q的必要不充分条件．