

还剩12页未读,
继续阅读
2020版新设计一轮复习数学(理)江苏专版讲义:第四章第六节简单的三角恒等变换
展开
第六节简单的三角恒等变换
1.常用的公式变形
(1)由(sin α±cos α)2=sin2α+cos2α±2sin αcos α=1±sin 2α.
(2)由(sin α±cos α)2=1±sin 2α
⇒
(3)tan α±tan β=tan(α±β)(1∓tan αtan β);
cos2α=,sin2α=.
(4)sin α±cos α=sin.
2.几个常用的恒等变换
(1)万能代换:sin α=;cos α=;tan α=.
(2)恒等式:tan ==.
[小题体验]
1.计算:cos2-=________.
解析:原式===.
答案:
2.已知sin=,sin=,则tan x=________.
解析:因为sin=,sin=,
两式展开相加得2sin xcos =, ①
两式相减得2cos xsin =-, ②
①②两式相除得tan x=-7.
答案:-7
1.在三角函数式化简时,要结合三角函数的性质进行考虑,易出现符号的差错.
2.三角恒等变换时,选择合适的公式会简化化简过程.易出现公式的不合理使用.
[小题纠偏]
1.(2019·镇江调研)已知x∈,且sin 2x=,则sin x-cos x=________.
解析:∵x∈,∴sin x<cos x,
又sin 2x=,∴sin x-cos x=-
=-=-.
答案:-
2.已知sin -cos =-,450°<α<540°,则tan =________.
解析:已知等式两边平方得sin α=,又450°<α<540°,所以cos α=-,所以tan ==2.
答案:2
[题组练透]
1.化简:=________.
解析:原式==2cos α.
答案:2cos α
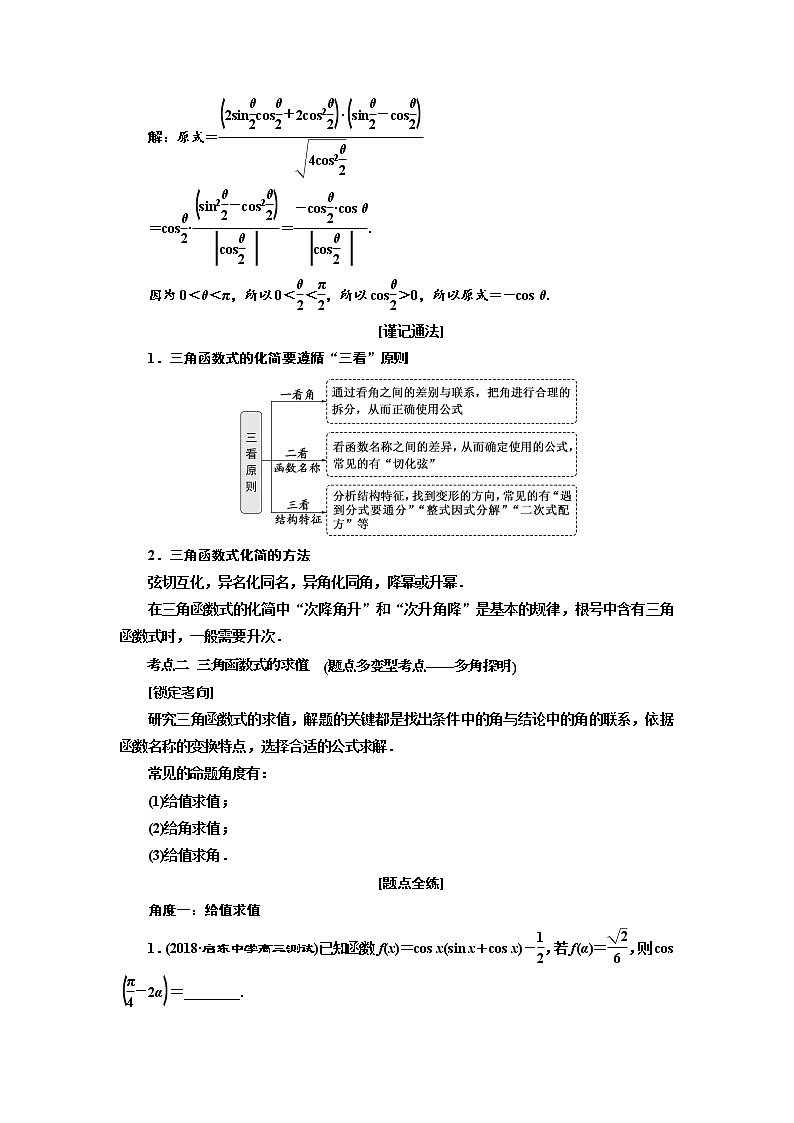
2.化简:(0<θ<π).
解:原式=
=cos·=.
因为0<θ<π,所以0<<,所以cos>0,所以原式=-cos θ.
[谨记通法]
1.三角函数式的化简要遵循“三看”原则
2.三角函数式化简的方法
弦切互化,异名化同名,异角化同角,降幂或升幂.
在三角函数式的化简中“次降角升”和“次升角降”是基本的规律,根号中含有三角函数式时,一般需要升次.
[锁定考向]
研究三角函数式的求值,解题的关键都是找出条件中的角与结论中的角的联系,依据函数名称的变换特点,选择合适的公式求解.
常见的命题角度有:
(1)给值求值;
(2)给角求值;
(3)给值求角.
[题点全练]
角度一:给值求值
1.(2018·启东中学高三测试)已知函数f(x)=cos x(sin x+cos x)-,若f(α)=,则cos=________.
解析:法一:f(x)=cos x(sin x+cos x)-=sin xcos x+cos2x-=sin 2x+-=sin 2x+cos 2x=sin,因为f(α)=,所以sin=,所以cos=cos=sin=.
法二:f(x)=cos x(sin x+cos x)-=sin xcos x+cos2x-=sin 2x+-= sin 2x+cos 2x,因为f(α)=,所以sin 2α+cos 2α=,
所以cos=cos cos 2α+sin sin 2α=(cos 2α+sin 2α)=×=.
答案:
角度二:给角求值
2.化简:sin 50°(1+tan 10°)=________.
解析:sin 50°(1+tan 10°)
=sin 50°
=sin 50°×
=sin 50°×
=
===1.
答案:1
角度三:给值求角
3.若sin 2α=,sin(β-α)=,且α∈,β∈,则α+β=________.
解析:因为α∈,所以2α∈,
因为sin 2α=,所以2α∈.
所以α∈且cos 2α=-,
又因为sin(β-α)=,β∈,
所以β-α∈,cos(β-α)=-,
所以cos(α+β)=cos[(β-α)+2α]
=cos(β-α)cos 2α-sin(β-α)sin 2α
=×-×=,
又α+β∈,所以α+β=.
答案:
[通法在握]
三角函数求值的类型及解题策略
(1)“给值求值”:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题关键在于“变角”,使其角相同或具有某种关系.
(2)“给角求值”:一般所给出的角都是非特殊角,从表面上来看是很难的,但仔细观察非特殊角与特殊角总有一定关系,解题时,要利用观察得到的关系,结合公式转化为特殊角并且消除非特殊角的三角函数而得解.
(3)“给值求角”:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,最后确定角.
[演练冲关]
1.已知cos=,则cos=________.
解析:∵cos=sin=,
∴cos=1-2sin2=1-2×2=.
答案:
2.=________.
解析:原式===-.
答案:-
3.已知α∈,tan=,那么sin 2α+cos 2α=________.
解析:由tan=,知=,
所以tan 2α=-.
因为2α∈,所以sin 2α=,cos 2α=-.
所以sin 2α+cos 2α=-.
答案:-
[典例引领]
1. (2019·睢宁模拟)已知函数f(x)=cos xcos+sin2x-.
(1)求函数f(x)的单调递增区间;
(2)若x∈,f(x)=,求cos 2x的值.
解:(1)函数f(x)=cos xcos+sin2 x-=sin xcos x+-=sin,
令2kπ-≤2x-≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z,
故函数f(x)的单调递增区间为,k∈Z.
(2)∵x∈,∴2x-∈,
又f(x)=sin=,
∴cos= =,
∴cos 2x=cos=coscos-sin sin=×-×=.
2.已知函数f(x)=5sin xcos x-5cos2x+(其中x∈R),求:
(1)函数f(x)的单调区间;
(2)函数f(x)图象的对称轴和对称中心.
解:(1)因为f(x)=sin 2x-(1+cos 2x)+=5=5sin,
由2kπ-≤2x-≤2kπ+(k∈Z),
得kπ-≤x≤kπ+(k∈Z),
所以函数f(x)的单调增区间为(k∈Z).
由2kπ+≤2x-≤2kπ+(k∈Z),
得kπ+≤x≤kπ+(k∈Z),
所以函数f(x)的单调减区间为(k∈Z).
(2)由2x-=kπ+(k∈Z),得x=+(k∈Z),
所以函数f(x)的对称轴方程为x=+(k∈Z).
由2x-=kπ(k∈Z),得x=+(k∈Z),
所以函数f(x)的对称中心为(k∈Z).
[由题悟法]
三角恒等变换在研究三角函数性质中的2个注意点
(1)三角函数的性质问题,往往都要先化成f(x)=Asin(ωx+φ)+b的形式再求解.要注意在进行此步骤之前,如果函数解析式中出现α及其二倍角、半角或函数值的平方,应根据变换的难易程度去化简,往往要利用到二倍角公式、升幂或降幂公式,把解析式统一化成关于同一个角的三角函数式.
(2)要正确理解三角函数的性质,关键是记住三角函数的图象,根据图象并结合整体代入的基本思想即可求三角函数的单调性、最值与周期.
[即时应用]
(2019·南通中学检测)已知函数f(x)=cos2,g(x)=1+sin 2x.
(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(2x0)的值;
(2)求函数h(x)=f(x)+g(x),x∈的值域.
解:(1)f(x)=cos2=,
∵x=x0是函数y=f(x)图象的一条对称轴,
∴2x0+=kπ(k∈Z),∴2x0=kπ-(k∈Z),
∴g(2x0)=1+sin 4x0=1+sin=.
(2)h(x)=f(x)+g(x)=+1+sin 2x
=+=+sin,
∵x∈,∴2x+∈,
∴sin∈,
∴h(x)=+sin∈.
即函数h(x)在上的值域为.
一抓基础,多练小题做到眼疾手快
1.(2018·东台期末)已知α∈(0,π),tan α=2,则cos 2α+cos α=________.
解析:由α∈(0,π),tan α=2=,得α为锐角,
结合sin2α+cos2α=1,可得sin α=,cos α=,
∴cos 2α+cos α=2cos2α-1+cos α=2×-1+=.
答案:
2.(2018·苏州高三期中调研)已知tan=2,则cos 2α=________.
解析:cos 2α=sin=2sincos===-.
答案:-
3.(2018·通州期末)已知cos=,则sin=________.
解析:∵cos=,
∴sin=sin
=cos=2cos2-1
=2×2-1=-.
答案:-
4.化简:=________.
解析:原式=
===.
答案:
5.已知tan(3π-x)=2,则=________.
解析:由诱导公式得tan(3π-x)=-tan x=2,
故===-3.
答案:-3
6.(2019·宜兴检测)在△ABC中,A,B,C的对边分别为a,b,c,且满足4cos2- cos 2(B+C)=,则角A的大小为________.
解析:由4cos2-cos 2(B+C)=,
得2(1+cos A)-cos 2(π-A)=,
化简得4cos2A-4cos A+1=0,解得cos A=,
∵0<A<π,故A=.
答案:
二保高考,全练题型做到高考达标
1.(2018·金陵中学检测)已知sin=cos,则cos 2α=________.
解析:因为sin=cos,
所以cos α-sin α=cos α-sin α,
即sin α=-cos α,
所以tan α==-1,
所以cos 2α=cos2α-sin2α===0.
答案:0
2.(2019·苏州中学模拟)已知α∈,sin=,则tan 2α=________.
解析:由sin=-cos α=,可得cos α=-.
又α∈,∴sin α=,tan α==-,
∴tan 2α==.
答案:
3.(2018·通州期中)计算:tan 20°+tan 40°+tan 20°·tan 40°=________.
解析:tan 20°+tan 40°+tan 20°tan 40°=tan 60°(1-tan 20°tan 40°)+tan 20°tan 40°=-tan 20°tan 40°+tan 20°tan 40°=.
答案:
4.已知tan α,tan β是方程x2+3x+4=0的两根,且α,β∈,则α+β=________.
解析:由题意得tan α+tan β=-3<0,tan αtan β=4>0,
所以tan(α+β)==,且tan α<0,tan β<0,
又α,β∈,故α,β∈,
所以α+β∈(-π,0),所以α+β=-.
答案:-
5.(2019·如东中学月考)已知cos=,≤α≤,则cos=________.
解析:∵≤α≤,cos=>0,
∴<α+≤,
∴sin=- =-,
∴sin α=sin=sin-cos=-,
cos α=-=-,
∴cos 2α=2cos2α-1=-,sin 2α=2sin αcos α=,
则cos=cos 2α-sin 2α=-.
答案:-
6.已知cos(α+β)=,cos(α-β)=,则tan αtan β的值为________.
解析:因为cos(α+β)=,
所以cos αcos β-sin αsin β=.①
因为cos(α-β)=,
所以cos αcos β+sin αsin β=.②
①+②得cos αcos β=.
②-①得sin αsin β=.
所以tan αtan β==.
答案:
7.若tan α+=,α∈,则sin=________.
解析:由tan α+=,得+=,所以=,所以sin 2α=.因为α∈,所以2α∈,所以cos 2α=-.所以sin=sin 2αcos +cos 2αsin =×=-.
答案:-
8.(2019·南京模拟)若tan α+=,α∈,则sin+2coscos2α的值为________.
解析:∵tan α+=,α∈,
∴tan α=3或tan α=(舍去),
则sin+2coscos2α
=sin 2αcos+cos 2αsin+·
=sin 2α+cos 2α+
=·+·+
=·+·+
=×+×+=0.
答案:0
9.(2018·南通调研)已知sin=,α∈.
求:(1)cos α的值;
(2)sin的值.
解:(1)因为α∈,所以α+∈,
又sin=,
所以cos=- =- =-.
所以cos α=cos=coscos +sinsin =-×+×=-.
(2)因为α∈,cos α=-,
所以sin α== =.
所以sin 2α=2sin αcos α=2××=-,
cos 2α=2cos2α-1=2×2-1=-.
所以sin=sin 2αcos -cos 2αsin =×-×=-.
10.(2019·扬州调研)已知cos=,α∈.
(1)求sin α的值;
(2)若cos β=,β∈(0,π),求cos(α-2β)的值.
解:(1)∵cos=,α∈,
∴sin= =,
∴sin α=sin=sincos-cossin=×-×=.
(2)由(1)知cos α==,
∵cos β=,β∈(0,π),∴sin β==,
∴cos 2β=2cos2β-1=-,sin 2β=2sin βcos β=2××=,
∴cos(α-2β)=cos αcos 2β+sin αsin 2β=×+×=.
三上台阶,自主选做志在冲刺名校
1.(2018·启东高三测试)若sin 2α=2cos,则sin 2α=________.
解析:因为sin 2α=2cos,所以sin22α=4cos2,即sin22α=4×,所以sin22α=2(1+sin 2α),解得sin 2α=1±,显然sin 2α=1+不成立,所以sin 2α=1-.
答案:1-
2.化简:coscoscoscoscos=________.
解析:原式=-coscoscoscoscos
=-
=-===.
答案:
3.已知角α的顶点在坐标原点,始边与x轴的正半轴重合,终边经过点P(-3,).
(1)求sin 2α-tan α的值;
(2)若函数f(x)=cos(x-α)cos α-sin(x-α)sin α,求函数g(x)=f-2f 2(x)在区间上的值域.
解:(1)因为角α的终边经过点P(-3,),
所以sin α=,cos α=-,tan α=-.
所以sin 2α-tan α=2sin αcos α-tan α=-+=-.
(2)因为f(x)=cos(x-α)cos α-sin(x-α)sin α=cos x,x∈R,
所以g(x)=cos-2cos2x=sin 2x-1-cos 2x=2sin-1,
因为0≤x≤,所以-≤2x-≤.
所以-≤sin≤1,所以-2≤2sin-1≤1,
故函数g(x)=f-2f2(x)在区间上的值域是[-2,1].
1.常用的公式变形
(1)由(sin α±cos α)2=sin2α+cos2α±2sin αcos α=1±sin 2α.
(2)由(sin α±cos α)2=1±sin 2α
⇒
(3)tan α±tan β=tan(α±β)(1∓tan αtan β);
cos2α=,sin2α=.
(4)sin α±cos α=sin.
2.几个常用的恒等变换
(1)万能代换:sin α=;cos α=;tan α=.
(2)恒等式:tan ==.
[小题体验]
1.计算:cos2-=________.
解析:原式===.
答案:
2.已知sin=,sin=,则tan x=________.
解析:因为sin=,sin=,
两式展开相加得2sin xcos =, ①
两式相减得2cos xsin =-, ②
①②两式相除得tan x=-7.
答案:-7
1.在三角函数式化简时,要结合三角函数的性质进行考虑,易出现符号的差错.
2.三角恒等变换时,选择合适的公式会简化化简过程.易出现公式的不合理使用.
[小题纠偏]
1.(2019·镇江调研)已知x∈,且sin 2x=,则sin x-cos x=________.
解析:∵x∈,∴sin x<cos x,
又sin 2x=,∴sin x-cos x=-
=-=-.
答案:-
2.已知sin -cos =-,450°<α<540°,则tan =________.
解析:已知等式两边平方得sin α=,又450°<α<540°,所以cos α=-,所以tan ==2.
答案:2
[题组练透]
1.化简:=________.
解析:原式==2cos α.
答案:2cos α
2.化简:(0<θ<π).
解:原式=
=cos·=.
因为0<θ<π,所以0<<,所以cos>0,所以原式=-cos θ.
[谨记通法]
1.三角函数式的化简要遵循“三看”原则
2.三角函数式化简的方法
弦切互化,异名化同名,异角化同角,降幂或升幂.
在三角函数式的化简中“次降角升”和“次升角降”是基本的规律,根号中含有三角函数式时,一般需要升次.
[锁定考向]
研究三角函数式的求值,解题的关键都是找出条件中的角与结论中的角的联系,依据函数名称的变换特点,选择合适的公式求解.
常见的命题角度有:
(1)给值求值;
(2)给角求值;
(3)给值求角.
[题点全练]
角度一:给值求值
1.(2018·启东中学高三测试)已知函数f(x)=cos x(sin x+cos x)-,若f(α)=,则cos=________.
解析:法一:f(x)=cos x(sin x+cos x)-=sin xcos x+cos2x-=sin 2x+-=sin 2x+cos 2x=sin,因为f(α)=,所以sin=,所以cos=cos=sin=.
法二:f(x)=cos x(sin x+cos x)-=sin xcos x+cos2x-=sin 2x+-= sin 2x+cos 2x,因为f(α)=,所以sin 2α+cos 2α=,
所以cos=cos cos 2α+sin sin 2α=(cos 2α+sin 2α)=×=.
答案:
角度二:给角求值
2.化简:sin 50°(1+tan 10°)=________.
解析:sin 50°(1+tan 10°)
=sin 50°
=sin 50°×
=sin 50°×
=
===1.
答案:1
角度三:给值求角
3.若sin 2α=,sin(β-α)=,且α∈,β∈,则α+β=________.
解析:因为α∈,所以2α∈,
因为sin 2α=,所以2α∈.
所以α∈且cos 2α=-,
又因为sin(β-α)=,β∈,
所以β-α∈,cos(β-α)=-,
所以cos(α+β)=cos[(β-α)+2α]
=cos(β-α)cos 2α-sin(β-α)sin 2α
=×-×=,
又α+β∈,所以α+β=.
答案:
[通法在握]
三角函数求值的类型及解题策略
(1)“给值求值”:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题关键在于“变角”,使其角相同或具有某种关系.
(2)“给角求值”:一般所给出的角都是非特殊角,从表面上来看是很难的,但仔细观察非特殊角与特殊角总有一定关系,解题时,要利用观察得到的关系,结合公式转化为特殊角并且消除非特殊角的三角函数而得解.
(3)“给值求角”:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,最后确定角.
[演练冲关]
1.已知cos=,则cos=________.
解析:∵cos=sin=,
∴cos=1-2sin2=1-2×2=.
答案:
2.=________.
解析:原式===-.
答案:-
3.已知α∈,tan=,那么sin 2α+cos 2α=________.
解析:由tan=,知=,
所以tan 2α=-.
因为2α∈,所以sin 2α=,cos 2α=-.
所以sin 2α+cos 2α=-.
答案:-
[典例引领]
1. (2019·睢宁模拟)已知函数f(x)=cos xcos+sin2x-.
(1)求函数f(x)的单调递增区间;
(2)若x∈,f(x)=,求cos 2x的值.
解:(1)函数f(x)=cos xcos+sin2 x-=sin xcos x+-=sin,
令2kπ-≤2x-≤2kπ+,k∈Z,
得kπ-≤x≤kπ+,k∈Z,
故函数f(x)的单调递增区间为,k∈Z.
(2)∵x∈,∴2x-∈,
又f(x)=sin=,
∴cos= =,
∴cos 2x=cos=coscos-sin sin=×-×=.
2.已知函数f(x)=5sin xcos x-5cos2x+(其中x∈R),求:
(1)函数f(x)的单调区间;
(2)函数f(x)图象的对称轴和对称中心.
解:(1)因为f(x)=sin 2x-(1+cos 2x)+=5=5sin,
由2kπ-≤2x-≤2kπ+(k∈Z),
得kπ-≤x≤kπ+(k∈Z),
所以函数f(x)的单调增区间为(k∈Z).
由2kπ+≤2x-≤2kπ+(k∈Z),
得kπ+≤x≤kπ+(k∈Z),
所以函数f(x)的单调减区间为(k∈Z).
(2)由2x-=kπ+(k∈Z),得x=+(k∈Z),
所以函数f(x)的对称轴方程为x=+(k∈Z).
由2x-=kπ(k∈Z),得x=+(k∈Z),
所以函数f(x)的对称中心为(k∈Z).
[由题悟法]
三角恒等变换在研究三角函数性质中的2个注意点
(1)三角函数的性质问题,往往都要先化成f(x)=Asin(ωx+φ)+b的形式再求解.要注意在进行此步骤之前,如果函数解析式中出现α及其二倍角、半角或函数值的平方,应根据变换的难易程度去化简,往往要利用到二倍角公式、升幂或降幂公式,把解析式统一化成关于同一个角的三角函数式.
(2)要正确理解三角函数的性质,关键是记住三角函数的图象,根据图象并结合整体代入的基本思想即可求三角函数的单调性、最值与周期.
[即时应用]
(2019·南通中学检测)已知函数f(x)=cos2,g(x)=1+sin 2x.
(1)设x=x0是函数y=f(x)图象的一条对称轴,求g(2x0)的值;
(2)求函数h(x)=f(x)+g(x),x∈的值域.
解:(1)f(x)=cos2=,
∵x=x0是函数y=f(x)图象的一条对称轴,
∴2x0+=kπ(k∈Z),∴2x0=kπ-(k∈Z),
∴g(2x0)=1+sin 4x0=1+sin=.
(2)h(x)=f(x)+g(x)=+1+sin 2x
=+=+sin,
∵x∈,∴2x+∈,
∴sin∈,
∴h(x)=+sin∈.
即函数h(x)在上的值域为.
一抓基础,多练小题做到眼疾手快
1.(2018·东台期末)已知α∈(0,π),tan α=2,则cos 2α+cos α=________.
解析:由α∈(0,π),tan α=2=,得α为锐角,
结合sin2α+cos2α=1,可得sin α=,cos α=,
∴cos 2α+cos α=2cos2α-1+cos α=2×-1+=.
答案:
2.(2018·苏州高三期中调研)已知tan=2,则cos 2α=________.
解析:cos 2α=sin=2sincos===-.
答案:-
3.(2018·通州期末)已知cos=,则sin=________.
解析:∵cos=,
∴sin=sin
=cos=2cos2-1
=2×2-1=-.
答案:-
4.化简:=________.
解析:原式=
===.
答案:
5.已知tan(3π-x)=2,则=________.
解析:由诱导公式得tan(3π-x)=-tan x=2,
故===-3.
答案:-3
6.(2019·宜兴检测)在△ABC中,A,B,C的对边分别为a,b,c,且满足4cos2- cos 2(B+C)=,则角A的大小为________.
解析:由4cos2-cos 2(B+C)=,
得2(1+cos A)-cos 2(π-A)=,
化简得4cos2A-4cos A+1=0,解得cos A=,
∵0<A<π,故A=.
答案:
二保高考,全练题型做到高考达标
1.(2018·金陵中学检测)已知sin=cos,则cos 2α=________.
解析:因为sin=cos,
所以cos α-sin α=cos α-sin α,
即sin α=-cos α,
所以tan α==-1,
所以cos 2α=cos2α-sin2α===0.
答案:0
2.(2019·苏州中学模拟)已知α∈,sin=,则tan 2α=________.
解析:由sin=-cos α=,可得cos α=-.
又α∈,∴sin α=,tan α==-,
∴tan 2α==.
答案:
3.(2018·通州期中)计算:tan 20°+tan 40°+tan 20°·tan 40°=________.
解析:tan 20°+tan 40°+tan 20°tan 40°=tan 60°(1-tan 20°tan 40°)+tan 20°tan 40°=-tan 20°tan 40°+tan 20°tan 40°=.
答案:
4.已知tan α,tan β是方程x2+3x+4=0的两根,且α,β∈,则α+β=________.
解析:由题意得tan α+tan β=-3<0,tan αtan β=4>0,
所以tan(α+β)==,且tan α<0,tan β<0,
又α,β∈,故α,β∈,
所以α+β∈(-π,0),所以α+β=-.
答案:-
5.(2019·如东中学月考)已知cos=,≤α≤,则cos=________.
解析:∵≤α≤,cos=>0,
∴<α+≤,
∴sin=- =-,
∴sin α=sin=sin-cos=-,
cos α=-=-,
∴cos 2α=2cos2α-1=-,sin 2α=2sin αcos α=,
则cos=cos 2α-sin 2α=-.
答案:-
6.已知cos(α+β)=,cos(α-β)=,则tan αtan β的值为________.
解析:因为cos(α+β)=,
所以cos αcos β-sin αsin β=.①
因为cos(α-β)=,
所以cos αcos β+sin αsin β=.②
①+②得cos αcos β=.
②-①得sin αsin β=.
所以tan αtan β==.
答案:
7.若tan α+=,α∈,则sin=________.
解析:由tan α+=,得+=,所以=,所以sin 2α=.因为α∈,所以2α∈,所以cos 2α=-.所以sin=sin 2αcos +cos 2αsin =×=-.
答案:-
8.(2019·南京模拟)若tan α+=,α∈,则sin+2coscos2α的值为________.
解析:∵tan α+=,α∈,
∴tan α=3或tan α=(舍去),
则sin+2coscos2α
=sin 2αcos+cos 2αsin+·
=sin 2α+cos 2α+
=·+·+
=·+·+
=×+×+=0.
答案:0
9.(2018·南通调研)已知sin=,α∈.
求:(1)cos α的值;
(2)sin的值.
解:(1)因为α∈,所以α+∈,
又sin=,
所以cos=- =- =-.
所以cos α=cos=coscos +sinsin =-×+×=-.
(2)因为α∈,cos α=-,
所以sin α== =.
所以sin 2α=2sin αcos α=2××=-,
cos 2α=2cos2α-1=2×2-1=-.
所以sin=sin 2αcos -cos 2αsin =×-×=-.
10.(2019·扬州调研)已知cos=,α∈.
(1)求sin α的值;
(2)若cos β=,β∈(0,π),求cos(α-2β)的值.
解:(1)∵cos=,α∈,
∴sin= =,
∴sin α=sin=sincos-cossin=×-×=.
(2)由(1)知cos α==,
∵cos β=,β∈(0,π),∴sin β==,
∴cos 2β=2cos2β-1=-,sin 2β=2sin βcos β=2××=,
∴cos(α-2β)=cos αcos 2β+sin αsin 2β=×+×=.
三上台阶,自主选做志在冲刺名校
1.(2018·启东高三测试)若sin 2α=2cos,则sin 2α=________.
解析:因为sin 2α=2cos,所以sin22α=4cos2,即sin22α=4×,所以sin22α=2(1+sin 2α),解得sin 2α=1±,显然sin 2α=1+不成立,所以sin 2α=1-.
答案:1-
2.化简:coscoscoscoscos=________.
解析:原式=-coscoscoscoscos
=-
=-===.
答案:
3.已知角α的顶点在坐标原点,始边与x轴的正半轴重合,终边经过点P(-3,).
(1)求sin 2α-tan α的值;
(2)若函数f(x)=cos(x-α)cos α-sin(x-α)sin α,求函数g(x)=f-2f 2(x)在区间上的值域.
解:(1)因为角α的终边经过点P(-3,),
所以sin α=,cos α=-,tan α=-.
所以sin 2α-tan α=2sin αcos α-tan α=-+=-.
(2)因为f(x)=cos(x-α)cos α-sin(x-α)sin α=cos x,x∈R,
所以g(x)=cos-2cos2x=sin 2x-1-cos 2x=2sin-1,
因为0≤x≤,所以-≤2x-≤.
所以-≤sin≤1,所以-2≤2sin-1≤1,
故函数g(x)=f-2f2(x)在区间上的值域是[-2,1].
相关资料
更多








