

还剩15页未读,
继续阅读
所属成套资源:2021高考数学理科人教A版一轮复习学案作业
成套系列资料,整套一键下载
2021高考数学(理)人教A版一轮复习学案作业:第九章9.6双曲线
展开
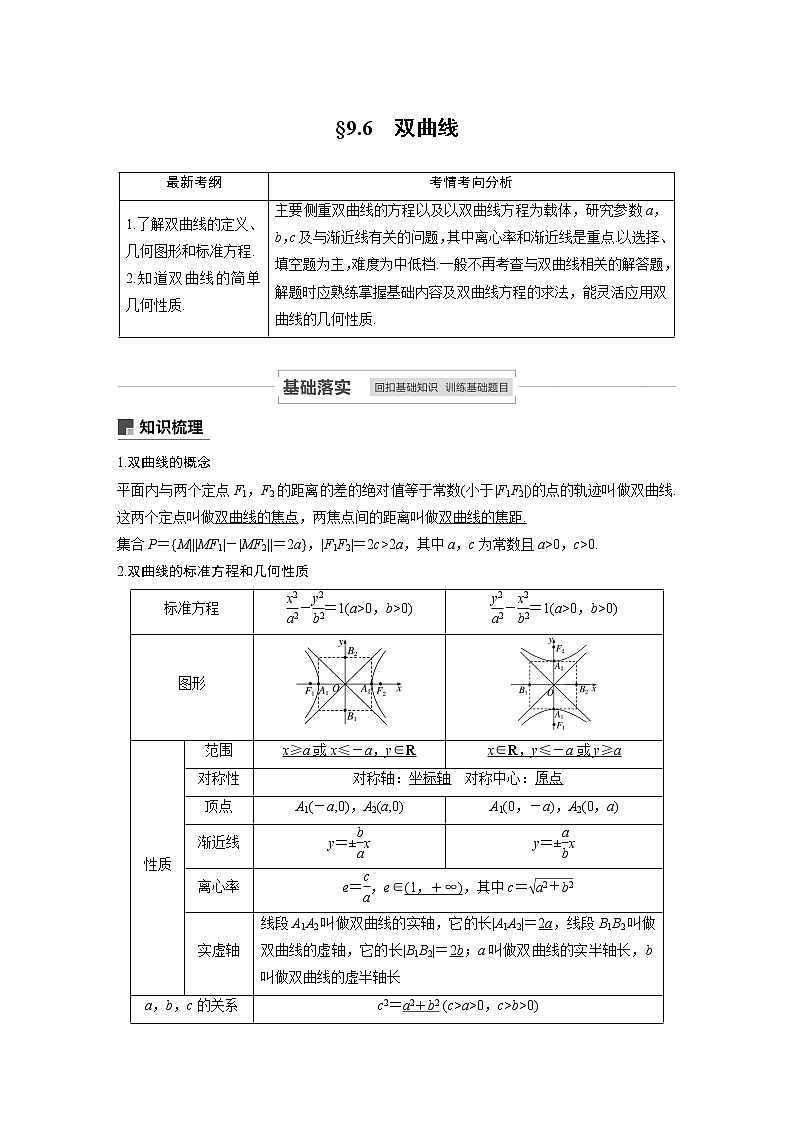
§9.6 双曲线
最新考纲
考情考向分析
1.了解双曲线的定义、几何图形和标准方程.
2.知道双曲线的简单几何性质.
主要侧重双曲线的方程以及以双曲线方程为载体,研究参数a,b,c及与渐近线有关的问题,其中离心率和渐近线是重点.以选择、填空题为主,难度为中低档.一般不再考查与双曲线相关的解答题,解题时应熟练掌握基础内容及双曲线方程的求法,能灵活应用双曲线的几何性质.
1.双曲线的概念
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c>2a,其中a,c为常数且a>0,c>0.
2.双曲线的标准方程和几何性质
标准方程
-=1(a>0,b>0)
-=1(a>0,b>0)
图形
性质
范围
x≥a或x≤-a,y∈R
x∈R,y≤-a或y≥a
对称性
对称轴:坐标轴 对称中心:原点
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
渐近线
y=±x
y=±x
离心率
e=,e∈(1,+∞),其中c=
实虚轴
线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a,线段B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;a叫做双曲线的实半轴长,b叫做双曲线的虚半轴长
a,b,c的关系
c2=a2+b2 (c>a>0,c>b>0)
概念方法微思考
1.平面内与两定点F1,F2的距离之差的绝对值等于常数2a的动点的轨迹一定为双曲线吗?为什么?
提示 不一定.当2a=|F1F2|时,动点的轨迹是两条射线;
当2a>|F1F2|时,动点的轨迹不存在;
当2a=0时,动点的轨迹是线段F1F2的中垂线.
2.与椭圆标准方程相比较,双曲线标准方程中,a,b只限制a>0,b>0,二者没有大小要求,若a>b>0,a=b>0,00时,e=(亦称等轴双曲线);当0.
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)平面内到点F1(0,4),F2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线.( × )
(2)方程-=1(mn>0)表示焦点在x轴上的双曲线.( × )
(3)双曲线方程-=λ(m>0,n>0,λ≠0)的渐近线方程是-=0,即±=0.( √ )
(4)等轴双曲线的渐近线互相垂直,离心率等于.( √ )
题组二 教材改编
2.若双曲线-=1(a>0,b>0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( )
A. B.5 C. D.2
答案 A
解析 由题意知焦点到其渐近线的距离等于实轴长,双曲线的渐近线方程为±=0,
即bx±ay=0,
∴2a==b.又a2+b2=c2,∴5a2=c2.
∴e2==5,∴e=.
3.已知a>b>0,椭圆C1的方程为+=1,双曲线C2的方程为-=1,C1与C2的离心率之积为,则C2的渐近线方程为( )
A.x±y=0
B.x±y=0
C.x±2y=0
D.2x±y=0
答案 A
解析 椭圆C1的离心率为,双曲线C2的离心率为,所以·=,即a4=4b4,所以a=b,所以双曲线C2的渐近线方程是y=±x,即x±y=0.
4.经过点A(4,1),且对称轴都在坐标轴上的等轴双曲线方程为________.
答案 -=1
解析 设双曲线的方程为-=±1(a>0),
把点A(4,1)代入,得a2=15(舍负),
故所求方程为-=1.
题组三 易错自纠
5.已知双曲线的实轴长为8,离心率为2,则双曲线的标准方程为________.
答案 -=1或-=1
解析 由题意知a=4,e==2,
∴c=8,
∴b2=c2-a2=64-16=48.
因为双曲线的焦点位置不确定,故所求双曲线的标准方程为-=1或-=1.
6.P是双曲线-=1上任意一点,F1,F2分别是它的左、右焦点,且|PF1|=9,则|PF2|=________.
答案 17
解析 由题意知a=4,b=9,
c==,
由于|PF1|=9
∴|PF2|=|PF1|+8=17.
双曲线的定义
例1 (1)已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,则动圆圆心M的轨迹方程为________________.
答案 x2-=1(x≤-1)
解析 如图所示,设动圆M与圆C1及圆C2分别外切于A和B.
根据两圆外切的条件,
得|MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|,
因为|MA|=|MB|,
所以|MC1|-|AC1|=|MC2|-|BC2|,
即|MC2|-|MC1|=|BC2|-|AC1|=2,
所以点M到两定点C2,C1的距离的差是常数且小于|C1C2|=6.
又根据双曲线的定义,得动点M的轨迹为双曲线的左支(点M与C2的距离大,与C1的距离小),
其中a=1,c=3,则b2=8.
故点M的轨迹方程为x2-=1(x≤-1).
(2)已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,∠F1PF2=60°,则△F1PF2的面积为______.
答案 2
解析 不妨设点P在双曲线的右支上,
则|PF1|-|PF2|=2a=2,
在△F1PF2中,由余弦定理,得
cos∠F1PF2==,
∴|PF1|·|PF2|=8,
∴=|PF1|·|PF2|·sin 60°=2.
本例(2)中,“∠F1PF2=60°”改为“·=0”,则△F1PF2的面积为____.
答案 2
解析 不妨设点P在双曲线的右支上,
则|PF1|-|PF2|=2a=2,
∵·=0,∴⊥,
∴在△F1PF2中,有|PF1|2+|PF2|2=|F1F2|2,
即|PF1|2+|PF2|2=16,
∴|PF1|·|PF2|=4,
∴=|PF1|·|PF2|=2.
思维升华 在“焦点三角形”中,常利用正弦定理、余弦定理,结合||PF1|-|PF2||=2a,运用平方的方法,建立与|PF1|·|PF2|的联系.
跟踪训练1 (1)(2020·广东普宁华侨中学期末)过双曲线x2-=1的左焦点F1作一条直线l交双曲线左支于P,Q两点,若|PQ|=4,F2是双曲线的右焦点,则△PF2Q的周长是______.
答案 12
解析 由题意,得|PF2|-|PF1|=2,|QF2|-|QF1|=2.
∵|PF1|+|QF1|=|PQ|=4,
∴|PF2|+|QF2|-4=4,
∴|PF2|+|QF2|=8.
∴△PF2Q的周长是|PF2|+|QF2|+|PQ|=8+4=12.
(2)已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=________.
答案
解析 ∵由双曲线的定义得|PF1|-|PF2|=|PF2|=2a=2,
∴|PF1|=2|PF2|=4,
则cos∠F1PF2===.
双曲线的标准方程
1.(2020·合肥调研)已知双曲线的渐近线为y=±x,实轴长为4,则该双曲线的方程为( )
A.-=1 B.-=1或-=1
C.-=1 D.-=1或-=1
答案 D
解析 设双曲线方程为-=1(m≠0),
又2a=4,∴a2=4,
当m>0时,2m=4,m=2;当m<0时,-m=4,m=-4.
故所求双曲线方程为-=1或-=1.
2.(2017·全国Ⅲ)已知双曲线C:-=1(a>0,b>0)的一条渐近线方程为y=x,且与椭圆+=1有公共焦点,则C的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
答案 B
解析 由y=x,可得=.①
由椭圆+=1的焦点为(3,0),(-3,0),
可得a2+b2=9.②
由①②可得a2=4,b2=5.
所以C的方程为-=1.故选B.
3.经过点P(-3,2)和点Q(-6,-7)的双曲线方程为________.
答案 -=1
解析 设双曲线方程为mx2-ny2=1(mn>0),
∴解得
∴双曲线方程为-=1.
4.过双曲线C:-=1(a>b>0)的右顶点作x轴的垂线,与C的一条渐近线相交于点A.若以C的右焦点F为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的标准方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
答案 A
解析 因为渐近线y=x与直线x=a交于点A(a,b),c=4且=4,解得a2=4,b2=12,因此双曲线的标准方程为-=1.
思维升华 求双曲线的标准方程的方法
(1)定义法:由题目条件判断出动点轨迹是双曲线,由双曲线定义,确定2a,2b或2c,从而求出a2,b2,写出双曲线方程.
(2)待定系数法:先确定焦点在x轴还是y轴,设出标准方程,再由条件确定a2,b2的值,即“先定型,再定量”,如果焦点位置不好确定,可将双曲线方程设为-=λ(λ≠0),再根据条件求λ的值.
注意 ①双曲线与椭圆标准方程均可记为mx2+ny2=1(mn≠0),其中当m>0,n>0,且m≠n时表示椭圆;当mn<0时表示双曲线,合理使用这种形式可避免讨论.
②常见双曲线设法
(i)已知a=b的双曲线可设为x2-y2=λ(λ≠0);
(ii)已知过两点的双曲线可设为Ax2-By2=1(AB>0);
(iii)已知渐近线为±=0的双曲线方程可设为-=λ(λ≠0).
双曲线的几何性质
命题点1 渐近线
例2 (1)(2019·包头青山区模拟)已知双曲线9y2-m2x2=1(m>0)的一个顶点到它的一条渐近线的距离为,则m等于( )
A.1 B.2 C.3 D.4
答案 D
解析 由已知,取顶点,渐近线3y-mx=0,则顶点到渐近线的距离为=,解得m=4.
(2)(2020·湖北八市重点高中联考)已知双曲线C:-=1(a>0,b>0)的左、右顶点分别为A,B,点P在曲线C上,若△PAB中,∠PBA=∠PAB+,则双曲线C的渐近线方程为_______.
答案 y=±x
解析 如图,过B作BM⊥x轴,
∵∠PBA=∠PAB+,则∠PAB=∠PBM,
∴∠PAB+∠PBx=,即kPA·kPB=1.
设P(x,y),又A(-a,0),B(a,0),·=1,∴x2-y2=a2,
∴a=b,则双曲线C的渐近线方程为y=±x,
思维升华 求双曲线的渐近线的方法
求双曲线-=1(a>0,b>0)或-=1(a>0,b>0)的渐近线方程的方法是令右边的常数等于0,即令-=0,得y=±x;或令-=0,得y=±x.反之,已知渐近线方程为y=±x,可设双曲线方程为-=λ(a>0,b>0,λ≠0).
命题点2 离心率
例3 (1)(2019·浙江)渐近线方程为x±y=0的双曲线的离心率是( )
A. B.1 C. D.2
答案 C
解析 因为双曲线的渐近线方程为x±y=0,所以无论双曲线的焦点在x轴上还是在y轴上,都满足a=b,所以c=a,所以双曲线的离心率e==.
(2)(2019·唐山模拟)设双曲线C:-=1(a>b>0)的两条渐近线的夹角为α,且cos α=,则C的离心率为( )
A. B. C. D.2
答案 B
解析 ∵a>b>0,∴渐近线y=x的斜率小于1,
∵两条渐近线的夹角为α,cos α=.
∴cos2=,sin2=,tan2=,
∴=,∴=,∴e2=,∴e=.
(3)(2019·全国Ⅱ)设F为双曲线C:-=1(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P,Q两点.若|PQ|=|OF|,则C的离心率为( )
A. B. C.2 D.
答案 A
解析 如图,由题意知,以OF为直径的圆的方程为2+y2=,①
将x2+y2=a2,②
①-②得x=,
则以OF为直径的圆与圆x2+y2=a2的相交弦所在直线的方程为x=,
所以|PQ|=2.
由|PQ|=|OF|,得2=c,
整理得c4-4a2c2+4a4=0,即e4-4e2+4=0,解得e=,故选A.
(4)(2019·全国Ⅰ)已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若=,·=0,则C的离心率为________.
答案 2
解析 因为·=0,所以F1B⊥F2B,如图.因为=,所以点A为F1B的中点,又点O为F1F2的中点,所以OA∥BF2,所以F1B⊥OA,所以|OF1|=|OB|,所以∠BF1O=∠F1BO,所以∠BOF2=2∠BF1O.因为直线OA,OB为双曲线C的两条渐近线,
所以tan∠BOF2=,tan∠BF1O=.
因为tan∠BOF2=tan(2∠BF1O),
所以=,所以b2=3a2,
所以c2-a2=3a2,
即2a=c,所以双曲线的离心率e==2.
思维升华 求双曲线的离心率
(1)求双曲线的离心率或其范围的方法
①求a,b,c的值,由==1+直接求e.
②列出含有a,b,c的等式(或不等式),借助于b2=c2-a2消去b,然后转化成关于e的方程(或不等式)求解.
(2)焦点在x轴上的双曲线的渐近线的斜率k与离心率e的关系:k====.
跟踪训练2 (1)(2019·陕西汉中模拟)若双曲线x2-=1(m>0)的焦点到渐近线的距离是4,则m的值是( )
A.2 B. C.1 D.4
答案 D
解析 双曲线x2-=1(m>0)的焦点设为(c,0),
当双曲线方程为-=1时,
渐近线方程设为bx-ay=0,可得焦点到渐近线的距离
d==b,
故由题意可得b=m=4.
(2)(2019·安徽江淮十校模拟)已知点(1,2)是双曲线-=1(a>0,b>0)上一点,则其离心率的取值范围是( )
A. B.
C. D.
答案 C
解析 已知点(1,2)是双曲线-=1(a>0,b>0)上一点,得-=1,
即=b2+4,
所以e===>,所以e>.
(3)(2019·天津)已知抛物线y2=4x的焦点为F,准线为l.若l与双曲线-=1(a>0,b>0)的两条渐近线分别交于点A和点B,且|AB|=4|OF|(O为原点),则双曲线的离心率为( )
A. B. C.2 D.
答案 D
解析 由题意,可得F(1,0),直线l的方程为x=-1,双曲线的渐近线方程为y=±x.将x=-1代入y=±x,得y=±,所以点A,B的纵坐标的绝对值均为.由|AB|=4|OF|可得=4,即b=2a,b2=4a2,故双曲线的离心率e===.
1.(2020·衡水质检)对于实数m,“1
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 C
解析 若方程+=1表示双曲线,
则(m-1)(m-2)<0,得1
A. B.
C. D.-1
答案 B
解析 因为a,b,c成等比数列,
所以b2=ac,即c2-a2=ac,
e2-1=e,所以e2-e-1=0,
因为e∈(1,+∞),所以e=.
3.已知双曲线-=1(a>0,b>0)的离心率为2,则该双曲线的渐近线方程为( )
A.x±y=0 B.x±y=0
C.x±y=0 D.2x±y=0
答案 C
解析 ∵双曲线的方程是-=1(a>0,b>0),
∴双曲线的渐近线方程为y=±x.
又∵离心率e==2,
∴c=2a,∴b==a.
由此可得双曲线的渐近线方程为y=±x=±x,
即x±y=0.故选C.
4.已知方程-=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是( )
A.(-1,3) B.(-1,)
C.(0,3) D.(0,)
答案 A
解析 由题意得(m2+n)(3m2-n)>0,
解得-m2
得m2+n+3m2-n=4,
即m2=1,所以-1
A.x2-5y2=1 B.5y2-x2=1
C.5x2-y2=1 D.y2-5x2=1
答案 C
解析 因为抛物线的焦点为(1,0),
所以解得
所以双曲线方程为5x2-=1.
6.(2019·全国100所名校冲刺卷)已知双曲线C:-y2=1(a>0),O为坐标原点,以其实轴为直径的⊙O与一渐近线相交于两点,其中一点为P,过P且与⊙O相切的直线与x轴交于点A,若|OA|=,则该双曲线的渐近线方程为( )
A.x±y=0 B.3x±y=0 C.x±y=0 D.x±3y=0
答案 D
解析 根据双曲线的几何意义知c=,所以a=3,
所以双曲线的渐近线方程为y=±x,即x±3y=0.
7.(2019·全国Ⅲ)双曲线C:-=1的右焦点为F,点P在C的一条渐近线上,O为坐标原点.若|PO|=|PF|,则△PFO的面积为( )
A. B. C.2 D.3
答案 A
解析 不妨设点P在第一象限,根据题意可知c2=6,
所以|OF|=.
又tan∠POF==,所以等腰△POF的高h=×=,
所以S△PFO=××=.
8.(2019·成都模拟)已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),又点N .若双曲线C左支上的任意一点M均满足|MF2|+|MN|>4b,则双曲线C的离心率的取值范围为( )
A.
B.
C.(1,)∪(,+∞)
D.∪(,+∞)
答案 D
解析 由双曲线的定义可得,|MF2|-|MF1|=2a.
由题意,双曲线C左支上的任意一点M均满足|MF2|+|MN|>4b,
即双曲线C左支上的任意一点M均满足|MF1|+|MN|>4b-2a,
而|MF1|+|MN|≥|F1N|,
从而|F1N|>4b-2a,即>4b-2a,
整理得,32-+4>0,
即>0.
所以<或>2.
又e=,所以1.
9.(2019·安徽江淮十校联考)已知点(1,2)是双曲线-=1(a>0,b>0)渐近线上一点,则其离心率是________.
答案
解析 因为点(1,2)是双曲线-=1(a>0,b>0)渐近线上一点,
所以,渐近线方程为y=2x,所以=2,
因此,e===.
10.(2020·焦作模拟)已知左、右焦点分别为F1,F2的双曲线C:-=1(a>0,b>0)的一条渐近线与直线l:x-2y=0相互垂直,点P在双曲线C上,且|PF1|-|PF2|=3,则双曲线C的焦距为________.
答案 3
解析 双曲线C:-=1(a>0,b>0)的渐近线为y=±x,
一条渐近线与直线l:x-2y=0相互垂直,可得=2,
即b=2a,由双曲线的定义可得2a=|PF1|-|PF2|=3,
可得a=,b=3,
即有c===,
即焦距为2c=3.
11.(2019·衡水调研)已知双曲线C:-=1(a>0,b>0)的实轴长为2,若双曲线C有两条渐近线与圆Ω:x2+y2=2交于M,N,P,Q四个点,且矩形MNPQ的面积为b,则双曲线C的离心率为________.
答案 2
解析 由题意得2a=2,则a=1,
故双曲线C的渐近线方程为y=±bx,设第一象限的交点为N(x0,y0),
则解得x=.
又矩形MNPQ的面积为2x0·2y0=4x0y0==b,
解得b=,
故c==2,
所以双曲线C的离心率为2.
12.(2020·临川一中模拟)已知双曲线-=1(a>0,b>0)中,A1,A2是左、右顶点,F是右焦点,B是虚轴的上端点.若在线段BF上(不含端点)存在不同的两点Pi(i=1,2),使得·=0,则双曲线离心率的取值范围是________.
答案
解析 设c为半焦距,则F(c,0),又B(0,b),
所以BF:bx+cy-bc=0,
以A1A2为直径的圆的方程为⊙O:x2+y2=a2,
因为·=0,i=1,2,
所以⊙O与线段BF有两个交点(不含端点),
所以即
故解得
13.(2020·黄山模拟)双曲线-=1(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(2,1)在“右”区域内,则双曲线离心率e的取值范围是( )
A. B.
C. D.
答案 B
解析 依题意知,双曲线-=1的渐近线方程为y=±x,且“右”区域由不等式组确定,又点(2,1)在“右”区域内,所以1<,即>,因此双曲线的离心率e=∈.
14.(2019·江南十校联考)已知双曲线C1,C2的焦点分别在x轴,y轴上,渐近线方程都为y=±x(a>0),离心率分别为e1,e2,则e1+e2的最小值为________.
答案 2
解析 由题意得双曲线C1的方程为-y2=t(a>0,t>0),
双曲线C2的方程为y2-=λ(a>0,λ>0),
所以e1==,e2==,
所以e1+e2=+≥2=2≥2(当且仅当a=1时等号成立).
15.(2020·广东华附、省实、广雅、深中联考)过双曲线-=1(a>0,b>0)的左焦点F(-c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,O为坐标原点,若=(+),则双曲线的离心率为( )
A. B. C. D.
答案 A
解析 ∵|OF|=c,|OE|=a,OE⊥EF,
∴|EF|==b,
∵=(+),
∴E为PF的中点,|OP|=|OF|=c,|PF|=2b,
设F′(c,0)为双曲线的右焦点,也为抛物线的焦点,
则EO为△PFF′的中位线,
则|PF′|=2|OE|=2a,可设P的坐标为(m,n),
则有n2=4cm,
由抛物线的定义可得|PF′|=m+c=2a,
m=2a-c,n2=4c(2a-c),
又|OP|=c,即有c2=(2a-c)2+4c(2a-c),
化简可得,c2-ac-a2=0,即e2-e-1=0,
由于e>1,解得e=.
16.(2020·长沙雅礼中学模拟)已知F是双曲线C:x2-=1的右焦点,P是C左支上一点,A(0,6),当△APF周长最小时,则点P的坐标为________.
答案 (-2,2)
解析 如图,由双曲线C的方程可知a2=1,b2=8,
∴c2=a2+b2=1+8=9,
∴c=3,
∴左焦点E(-3,0),
右焦点F(3,0),
∵|AF|==15,
∴当△APF的周长最小时,|PA|+|PF|最小.
由双曲线的性质得|PF|-|PE|=2a=2,
∴|PF|=|PE|+2,
又|PE|+|PA|≥|AE|=|AF|=15,当且仅当A,P,E三点共线且点P在线段AE上时,等号成立,
∴△APF的周长为|AF|+|AP|+|PF|=15+|PE|+|AP|+2≥15+15+2=32.
直线AE的方程为y=2x+6,将其代入到双曲线方程得x2+9x+14=0,解得x=-7(舍)或x=-2,
由x=-2,得y=2(负值已舍),
∴点P的坐标为(-2,2).
最新考纲
考情考向分析
1.了解双曲线的定义、几何图形和标准方程.
2.知道双曲线的简单几何性质.
主要侧重双曲线的方程以及以双曲线方程为载体,研究参数a,b,c及与渐近线有关的问题,其中离心率和渐近线是重点.以选择、填空题为主,难度为中低档.一般不再考查与双曲线相关的解答题,解题时应熟练掌握基础内容及双曲线方程的求法,能灵活应用双曲线的几何性质.
1.双曲线的概念
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c>2a,其中a,c为常数且a>0,c>0.
2.双曲线的标准方程和几何性质
标准方程
-=1(a>0,b>0)
-=1(a>0,b>0)
图形
性质
范围
x≥a或x≤-a,y∈R
x∈R,y≤-a或y≥a
对称性
对称轴:坐标轴 对称中心:原点
顶点
A1(-a,0),A2(a,0)
A1(0,-a),A2(0,a)
渐近线
y=±x
y=±x
离心率
e=,e∈(1,+∞),其中c=
实虚轴
线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a,线段B1B2叫做双曲线的虚轴,它的长|B1B2|=2b;a叫做双曲线的实半轴长,b叫做双曲线的虚半轴长
a,b,c的关系
c2=a2+b2 (c>a>0,c>b>0)
概念方法微思考
1.平面内与两定点F1,F2的距离之差的绝对值等于常数2a的动点的轨迹一定为双曲线吗?为什么?
提示 不一定.当2a=|F1F2|时,动点的轨迹是两条射线;
当2a>|F1F2|时,动点的轨迹不存在;
当2a=0时,动点的轨迹是线段F1F2的中垂线.
2.与椭圆标准方程相比较,双曲线标准方程中,a,b只限制a>0,b>0,二者没有大小要求,若a>b>0,a=b>0,0
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)平面内到点F1(0,4),F2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线.( × )
(2)方程-=1(mn>0)表示焦点在x轴上的双曲线.( × )
(3)双曲线方程-=λ(m>0,n>0,λ≠0)的渐近线方程是-=0,即±=0.( √ )
(4)等轴双曲线的渐近线互相垂直,离心率等于.( √ )
题组二 教材改编
2.若双曲线-=1(a>0,b>0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( )
A. B.5 C. D.2
答案 A
解析 由题意知焦点到其渐近线的距离等于实轴长,双曲线的渐近线方程为±=0,
即bx±ay=0,
∴2a==b.又a2+b2=c2,∴5a2=c2.
∴e2==5,∴e=.
3.已知a>b>0,椭圆C1的方程为+=1,双曲线C2的方程为-=1,C1与C2的离心率之积为,则C2的渐近线方程为( )
A.x±y=0
B.x±y=0
C.x±2y=0
D.2x±y=0
答案 A
解析 椭圆C1的离心率为,双曲线C2的离心率为,所以·=,即a4=4b4,所以a=b,所以双曲线C2的渐近线方程是y=±x,即x±y=0.
4.经过点A(4,1),且对称轴都在坐标轴上的等轴双曲线方程为________.
答案 -=1
解析 设双曲线的方程为-=±1(a>0),
把点A(4,1)代入,得a2=15(舍负),
故所求方程为-=1.
题组三 易错自纠
5.已知双曲线的实轴长为8,离心率为2,则双曲线的标准方程为________.
答案 -=1或-=1
解析 由题意知a=4,e==2,
∴c=8,
∴b2=c2-a2=64-16=48.
因为双曲线的焦点位置不确定,故所求双曲线的标准方程为-=1或-=1.
6.P是双曲线-=1上任意一点,F1,F2分别是它的左、右焦点,且|PF1|=9,则|PF2|=________.
答案 17
解析 由题意知a=4,b=9,
c==,
由于|PF1|=9
∴|PF2|=|PF1|+8=17.
双曲线的定义
例1 (1)已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆M同时与圆C1及圆C2相外切,则动圆圆心M的轨迹方程为________________.
答案 x2-=1(x≤-1)
解析 如图所示,设动圆M与圆C1及圆C2分别外切于A和B.
根据两圆外切的条件,
得|MC1|-|AC1|=|MA|,|MC2|-|BC2|=|MB|,
因为|MA|=|MB|,
所以|MC1|-|AC1|=|MC2|-|BC2|,
即|MC2|-|MC1|=|BC2|-|AC1|=2,
所以点M到两定点C2,C1的距离的差是常数且小于|C1C2|=6.
又根据双曲线的定义,得动点M的轨迹为双曲线的左支(点M与C2的距离大,与C1的距离小),
其中a=1,c=3,则b2=8.
故点M的轨迹方程为x2-=1(x≤-1).
(2)已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,∠F1PF2=60°,则△F1PF2的面积为______.
答案 2
解析 不妨设点P在双曲线的右支上,
则|PF1|-|PF2|=2a=2,
在△F1PF2中,由余弦定理,得
cos∠F1PF2==,
∴|PF1|·|PF2|=8,
∴=|PF1|·|PF2|·sin 60°=2.
本例(2)中,“∠F1PF2=60°”改为“·=0”,则△F1PF2的面积为____.
答案 2
解析 不妨设点P在双曲线的右支上,
则|PF1|-|PF2|=2a=2,
∵·=0,∴⊥,
∴在△F1PF2中,有|PF1|2+|PF2|2=|F1F2|2,
即|PF1|2+|PF2|2=16,
∴|PF1|·|PF2|=4,
∴=|PF1|·|PF2|=2.
思维升华 在“焦点三角形”中,常利用正弦定理、余弦定理,结合||PF1|-|PF2||=2a,运用平方的方法,建立与|PF1|·|PF2|的联系.
跟踪训练1 (1)(2020·广东普宁华侨中学期末)过双曲线x2-=1的左焦点F1作一条直线l交双曲线左支于P,Q两点,若|PQ|=4,F2是双曲线的右焦点,则△PF2Q的周长是______.
答案 12
解析 由题意,得|PF2|-|PF1|=2,|QF2|-|QF1|=2.
∵|PF1|+|QF1|=|PQ|=4,
∴|PF2|+|QF2|-4=4,
∴|PF2|+|QF2|=8.
∴△PF2Q的周长是|PF2|+|QF2|+|PQ|=8+4=12.
(2)已知F1,F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=________.
答案
解析 ∵由双曲线的定义得|PF1|-|PF2|=|PF2|=2a=2,
∴|PF1|=2|PF2|=4,
则cos∠F1PF2===.
双曲线的标准方程
1.(2020·合肥调研)已知双曲线的渐近线为y=±x,实轴长为4,则该双曲线的方程为( )
A.-=1 B.-=1或-=1
C.-=1 D.-=1或-=1
答案 D
解析 设双曲线方程为-=1(m≠0),
又2a=4,∴a2=4,
当m>0时,2m=4,m=2;当m<0时,-m=4,m=-4.
故所求双曲线方程为-=1或-=1.
2.(2017·全国Ⅲ)已知双曲线C:-=1(a>0,b>0)的一条渐近线方程为y=x,且与椭圆+=1有公共焦点,则C的方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
答案 B
解析 由y=x,可得=.①
由椭圆+=1的焦点为(3,0),(-3,0),
可得a2+b2=9.②
由①②可得a2=4,b2=5.
所以C的方程为-=1.故选B.
3.经过点P(-3,2)和点Q(-6,-7)的双曲线方程为________.
答案 -=1
解析 设双曲线方程为mx2-ny2=1(mn>0),
∴解得
∴双曲线方程为-=1.
4.过双曲线C:-=1(a>b>0)的右顶点作x轴的垂线,与C的一条渐近线相交于点A.若以C的右焦点F为圆心、半径为4的圆经过A,O两点(O为坐标原点),则双曲线C的标准方程为( )
A.-=1 B.-=1
C.-=1 D.-=1
答案 A
解析 因为渐近线y=x与直线x=a交于点A(a,b),c=4且=4,解得a2=4,b2=12,因此双曲线的标准方程为-=1.
思维升华 求双曲线的标准方程的方法
(1)定义法:由题目条件判断出动点轨迹是双曲线,由双曲线定义,确定2a,2b或2c,从而求出a2,b2,写出双曲线方程.
(2)待定系数法:先确定焦点在x轴还是y轴,设出标准方程,再由条件确定a2,b2的值,即“先定型,再定量”,如果焦点位置不好确定,可将双曲线方程设为-=λ(λ≠0),再根据条件求λ的值.
注意 ①双曲线与椭圆标准方程均可记为mx2+ny2=1(mn≠0),其中当m>0,n>0,且m≠n时表示椭圆;当mn<0时表示双曲线,合理使用这种形式可避免讨论.
②常见双曲线设法
(i)已知a=b的双曲线可设为x2-y2=λ(λ≠0);
(ii)已知过两点的双曲线可设为Ax2-By2=1(AB>0);
(iii)已知渐近线为±=0的双曲线方程可设为-=λ(λ≠0).
双曲线的几何性质
命题点1 渐近线
例2 (1)(2019·包头青山区模拟)已知双曲线9y2-m2x2=1(m>0)的一个顶点到它的一条渐近线的距离为,则m等于( )
A.1 B.2 C.3 D.4
答案 D
解析 由已知,取顶点,渐近线3y-mx=0,则顶点到渐近线的距离为=,解得m=4.
(2)(2020·湖北八市重点高中联考)已知双曲线C:-=1(a>0,b>0)的左、右顶点分别为A,B,点P在曲线C上,若△PAB中,∠PBA=∠PAB+,则双曲线C的渐近线方程为_______.
答案 y=±x
解析 如图,过B作BM⊥x轴,
∵∠PBA=∠PAB+,则∠PAB=∠PBM,
∴∠PAB+∠PBx=,即kPA·kPB=1.
设P(x,y),又A(-a,0),B(a,0),·=1,∴x2-y2=a2,
∴a=b,则双曲线C的渐近线方程为y=±x,
思维升华 求双曲线的渐近线的方法
求双曲线-=1(a>0,b>0)或-=1(a>0,b>0)的渐近线方程的方法是令右边的常数等于0,即令-=0,得y=±x;或令-=0,得y=±x.反之,已知渐近线方程为y=±x,可设双曲线方程为-=λ(a>0,b>0,λ≠0).
命题点2 离心率
例3 (1)(2019·浙江)渐近线方程为x±y=0的双曲线的离心率是( )
A. B.1 C. D.2
答案 C
解析 因为双曲线的渐近线方程为x±y=0,所以无论双曲线的焦点在x轴上还是在y轴上,都满足a=b,所以c=a,所以双曲线的离心率e==.
(2)(2019·唐山模拟)设双曲线C:-=1(a>b>0)的两条渐近线的夹角为α,且cos α=,则C的离心率为( )
A. B. C. D.2
答案 B
解析 ∵a>b>0,∴渐近线y=x的斜率小于1,
∵两条渐近线的夹角为α,cos α=.
∴cos2=,sin2=,tan2=,
∴=,∴=,∴e2=,∴e=.
(3)(2019·全国Ⅱ)设F为双曲线C:-=1(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P,Q两点.若|PQ|=|OF|,则C的离心率为( )
A. B. C.2 D.
答案 A
解析 如图,由题意知,以OF为直径的圆的方程为2+y2=,①
将x2+y2=a2,②
①-②得x=,
则以OF为直径的圆与圆x2+y2=a2的相交弦所在直线的方程为x=,
所以|PQ|=2.
由|PQ|=|OF|,得2=c,
整理得c4-4a2c2+4a4=0,即e4-4e2+4=0,解得e=,故选A.
(4)(2019·全国Ⅰ)已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1,F2,过F1的直线与C的两条渐近线分别交于A,B两点.若=,·=0,则C的离心率为________.
答案 2
解析 因为·=0,所以F1B⊥F2B,如图.因为=,所以点A为F1B的中点,又点O为F1F2的中点,所以OA∥BF2,所以F1B⊥OA,所以|OF1|=|OB|,所以∠BF1O=∠F1BO,所以∠BOF2=2∠BF1O.因为直线OA,OB为双曲线C的两条渐近线,
所以tan∠BOF2=,tan∠BF1O=.
因为tan∠BOF2=tan(2∠BF1O),
所以=,所以b2=3a2,
所以c2-a2=3a2,
即2a=c,所以双曲线的离心率e==2.
思维升华 求双曲线的离心率
(1)求双曲线的离心率或其范围的方法
①求a,b,c的值,由==1+直接求e.
②列出含有a,b,c的等式(或不等式),借助于b2=c2-a2消去b,然后转化成关于e的方程(或不等式)求解.
(2)焦点在x轴上的双曲线的渐近线的斜率k与离心率e的关系:k====.
跟踪训练2 (1)(2019·陕西汉中模拟)若双曲线x2-=1(m>0)的焦点到渐近线的距离是4,则m的值是( )
A.2 B. C.1 D.4
答案 D
解析 双曲线x2-=1(m>0)的焦点设为(c,0),
当双曲线方程为-=1时,
渐近线方程设为bx-ay=0,可得焦点到渐近线的距离
d==b,
故由题意可得b=m=4.
(2)(2019·安徽江淮十校模拟)已知点(1,2)是双曲线-=1(a>0,b>0)上一点,则其离心率的取值范围是( )
A. B.
C. D.
答案 C
解析 已知点(1,2)是双曲线-=1(a>0,b>0)上一点,得-=1,
即=b2+4,
所以e===>,所以e>.
(3)(2019·天津)已知抛物线y2=4x的焦点为F,准线为l.若l与双曲线-=1(a>0,b>0)的两条渐近线分别交于点A和点B,且|AB|=4|OF|(O为原点),则双曲线的离心率为( )
A. B. C.2 D.
答案 D
解析 由题意,可得F(1,0),直线l的方程为x=-1,双曲线的渐近线方程为y=±x.将x=-1代入y=±x,得y=±,所以点A,B的纵坐标的绝对值均为.由|AB|=4|OF|可得=4,即b=2a,b2=4a2,故双曲线的离心率e===.
1.(2020·衡水质检)对于实数m,“1
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 C
解析 若方程+=1表示双曲线,
则(m-1)(m-2)<0,得1
A. B.
C. D.-1
答案 B
解析 因为a,b,c成等比数列,
所以b2=ac,即c2-a2=ac,
e2-1=e,所以e2-e-1=0,
因为e∈(1,+∞),所以e=.
3.已知双曲线-=1(a>0,b>0)的离心率为2,则该双曲线的渐近线方程为( )
A.x±y=0 B.x±y=0
C.x±y=0 D.2x±y=0
答案 C
解析 ∵双曲线的方程是-=1(a>0,b>0),
∴双曲线的渐近线方程为y=±x.
又∵离心率e==2,
∴c=2a,∴b==a.
由此可得双曲线的渐近线方程为y=±x=±x,
即x±y=0.故选C.
4.已知方程-=1表示双曲线,且该双曲线两焦点间的距离为4,则n的取值范围是( )
A.(-1,3) B.(-1,)
C.(0,3) D.(0,)
答案 A
解析 由题意得(m2+n)(3m2-n)>0,
解得-m2
得m2+n+3m2-n=4,
即m2=1,所以-1
A.x2-5y2=1 B.5y2-x2=1
C.5x2-y2=1 D.y2-5x2=1
答案 C
解析 因为抛物线的焦点为(1,0),
所以解得
所以双曲线方程为5x2-=1.
6.(2019·全国100所名校冲刺卷)已知双曲线C:-y2=1(a>0),O为坐标原点,以其实轴为直径的⊙O与一渐近线相交于两点,其中一点为P,过P且与⊙O相切的直线与x轴交于点A,若|OA|=,则该双曲线的渐近线方程为( )
A.x±y=0 B.3x±y=0 C.x±y=0 D.x±3y=0
答案 D
解析 根据双曲线的几何意义知c=,所以a=3,
所以双曲线的渐近线方程为y=±x,即x±3y=0.
7.(2019·全国Ⅲ)双曲线C:-=1的右焦点为F,点P在C的一条渐近线上,O为坐标原点.若|PO|=|PF|,则△PFO的面积为( )
A. B. C.2 D.3
答案 A
解析 不妨设点P在第一象限,根据题意可知c2=6,
所以|OF|=.
又tan∠POF==,所以等腰△POF的高h=×=,
所以S△PFO=××=.
8.(2019·成都模拟)已知双曲线C:-=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0),又点N .若双曲线C左支上的任意一点M均满足|MF2|+|MN|>4b,则双曲线C的离心率的取值范围为( )
A.
B.
C.(1,)∪(,+∞)
D.∪(,+∞)
答案 D
解析 由双曲线的定义可得,|MF2|-|MF1|=2a.
由题意,双曲线C左支上的任意一点M均满足|MF2|+|MN|>4b,
即双曲线C左支上的任意一点M均满足|MF1|+|MN|>4b-2a,
而|MF1|+|MN|≥|F1N|,
从而|F1N|>4b-2a,即>4b-2a,
整理得,32-+4>0,
即>0.
所以<或>2.
又e=,所以1
9.(2019·安徽江淮十校联考)已知点(1,2)是双曲线-=1(a>0,b>0)渐近线上一点,则其离心率是________.
答案
解析 因为点(1,2)是双曲线-=1(a>0,b>0)渐近线上一点,
所以,渐近线方程为y=2x,所以=2,
因此,e===.
10.(2020·焦作模拟)已知左、右焦点分别为F1,F2的双曲线C:-=1(a>0,b>0)的一条渐近线与直线l:x-2y=0相互垂直,点P在双曲线C上,且|PF1|-|PF2|=3,则双曲线C的焦距为________.
答案 3
解析 双曲线C:-=1(a>0,b>0)的渐近线为y=±x,
一条渐近线与直线l:x-2y=0相互垂直,可得=2,
即b=2a,由双曲线的定义可得2a=|PF1|-|PF2|=3,
可得a=,b=3,
即有c===,
即焦距为2c=3.
11.(2019·衡水调研)已知双曲线C:-=1(a>0,b>0)的实轴长为2,若双曲线C有两条渐近线与圆Ω:x2+y2=2交于M,N,P,Q四个点,且矩形MNPQ的面积为b,则双曲线C的离心率为________.
答案 2
解析 由题意得2a=2,则a=1,
故双曲线C的渐近线方程为y=±bx,设第一象限的交点为N(x0,y0),
则解得x=.
又矩形MNPQ的面积为2x0·2y0=4x0y0==b,
解得b=,
故c==2,
所以双曲线C的离心率为2.
12.(2020·临川一中模拟)已知双曲线-=1(a>0,b>0)中,A1,A2是左、右顶点,F是右焦点,B是虚轴的上端点.若在线段BF上(不含端点)存在不同的两点Pi(i=1,2),使得·=0,则双曲线离心率的取值范围是________.
答案
解析 设c为半焦距,则F(c,0),又B(0,b),
所以BF:bx+cy-bc=0,
以A1A2为直径的圆的方程为⊙O:x2+y2=a2,
因为·=0,i=1,2,
所以⊙O与线段BF有两个交点(不含端点),
所以即
故解得
13.(2020·黄山模拟)双曲线-=1(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(2,1)在“右”区域内,则双曲线离心率e的取值范围是( )
A. B.
C. D.
答案 B
解析 依题意知,双曲线-=1的渐近线方程为y=±x,且“右”区域由不等式组确定,又点(2,1)在“右”区域内,所以1<,即>,因此双曲线的离心率e=∈.
14.(2019·江南十校联考)已知双曲线C1,C2的焦点分别在x轴,y轴上,渐近线方程都为y=±x(a>0),离心率分别为e1,e2,则e1+e2的最小值为________.
答案 2
解析 由题意得双曲线C1的方程为-y2=t(a>0,t>0),
双曲线C2的方程为y2-=λ(a>0,λ>0),
所以e1==,e2==,
所以e1+e2=+≥2=2≥2(当且仅当a=1时等号成立).
15.(2020·广东华附、省实、广雅、深中联考)过双曲线-=1(a>0,b>0)的左焦点F(-c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,O为坐标原点,若=(+),则双曲线的离心率为( )
A. B. C. D.
答案 A
解析 ∵|OF|=c,|OE|=a,OE⊥EF,
∴|EF|==b,
∵=(+),
∴E为PF的中点,|OP|=|OF|=c,|PF|=2b,
设F′(c,0)为双曲线的右焦点,也为抛物线的焦点,
则EO为△PFF′的中位线,
则|PF′|=2|OE|=2a,可设P的坐标为(m,n),
则有n2=4cm,
由抛物线的定义可得|PF′|=m+c=2a,
m=2a-c,n2=4c(2a-c),
又|OP|=c,即有c2=(2a-c)2+4c(2a-c),
化简可得,c2-ac-a2=0,即e2-e-1=0,
由于e>1,解得e=.
16.(2020·长沙雅礼中学模拟)已知F是双曲线C:x2-=1的右焦点,P是C左支上一点,A(0,6),当△APF周长最小时,则点P的坐标为________.
答案 (-2,2)
解析 如图,由双曲线C的方程可知a2=1,b2=8,
∴c2=a2+b2=1+8=9,
∴c=3,
∴左焦点E(-3,0),
右焦点F(3,0),
∵|AF|==15,
∴当△APF的周长最小时,|PA|+|PF|最小.
由双曲线的性质得|PF|-|PE|=2a=2,
∴|PF|=|PE|+2,
又|PE|+|PA|≥|AE|=|AF|=15,当且仅当A,P,E三点共线且点P在线段AE上时,等号成立,
∴△APF的周长为|AF|+|AP|+|PF|=15+|PE|+|AP|+2≥15+15+2=32.
直线AE的方程为y=2x+6,将其代入到双曲线方程得x2+9x+14=0,解得x=-7(舍)或x=-2,
由x=-2,得y=2(负值已舍),
∴点P的坐标为(-2,2).
相关资料
更多








