初中数学1.2 展开与折叠备课ppt课件

这是一份初中数学1.2 展开与折叠备课ppt课件，共33页。PPT课件主要包含了学习目标，正方体的11种展开图，一线不过四，田凹应弃之，相对两面不相连，“Z”端是对面，A和B为相对的两个面，拐角邻面知，C和D为相邻的两个面，“棒”在后面等内容，欢迎下载使用。

1.掌握正方体的展开图，能根据展开图判断立体模型.（重点）2.熟悉棱柱的展开图，初步尝试展开圆柱、圆锥的侧 面.（重点）3.熟悉几何体与它展开的平面图形的对应关系.(难点）
在生活中，我们经常见到正方体形状的盒子.
你知道这些正方体形状的盒子是怎样制作的吗？你能不能制作一个？
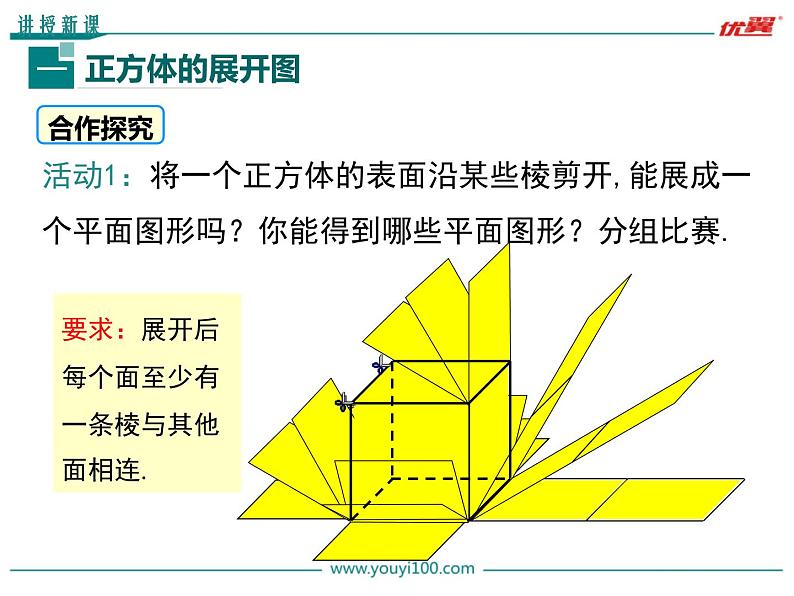
活动1：将一个正方体的表面沿某些棱剪开,能展成一个平面图形吗？你能得到哪些平面图形？分组比赛.
要求：展开后每个面至少有一条棱与其他面相连.
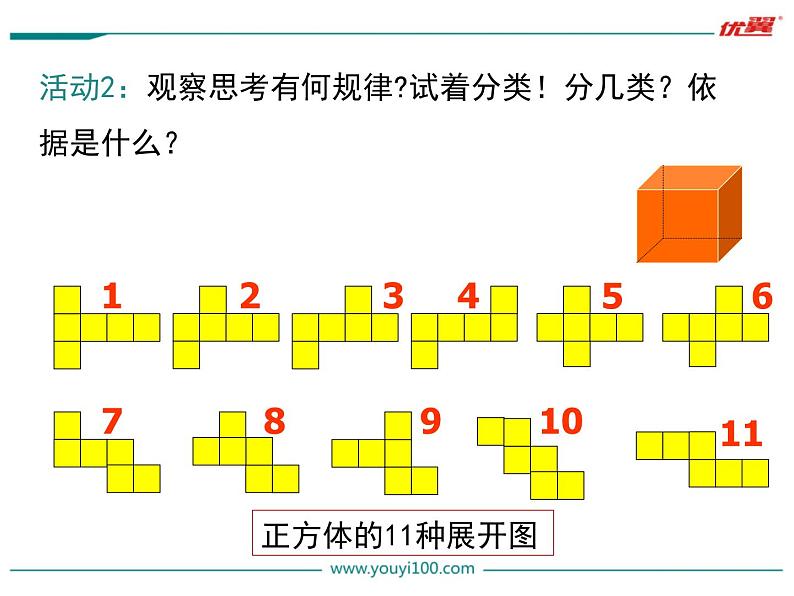
活动2：观察思考有何规律?试着分类！分几类？依据是什么？
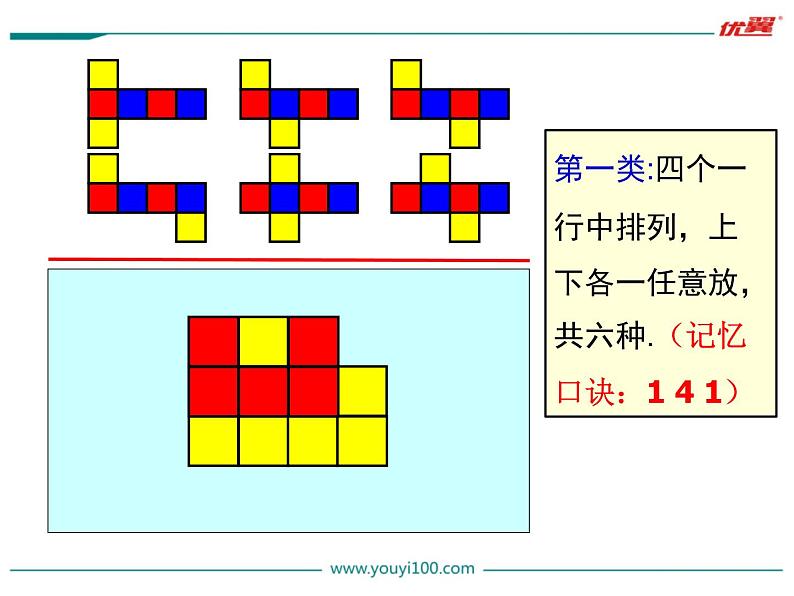
第一类:四个一行中排列，上下各一任意放，共六种.（记忆口诀：1 4 1）
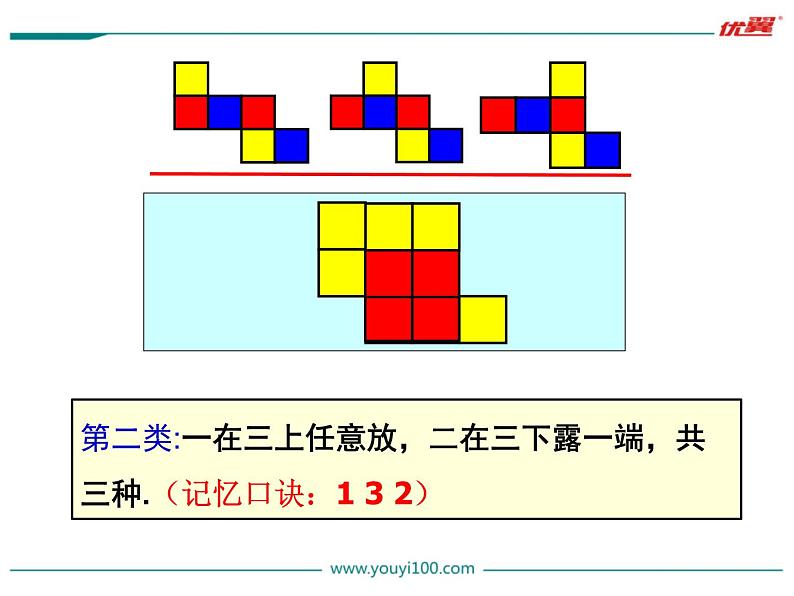
第二类:一在三上任意放，二在三下露一端，共三种.（记忆口诀：1 3 2）
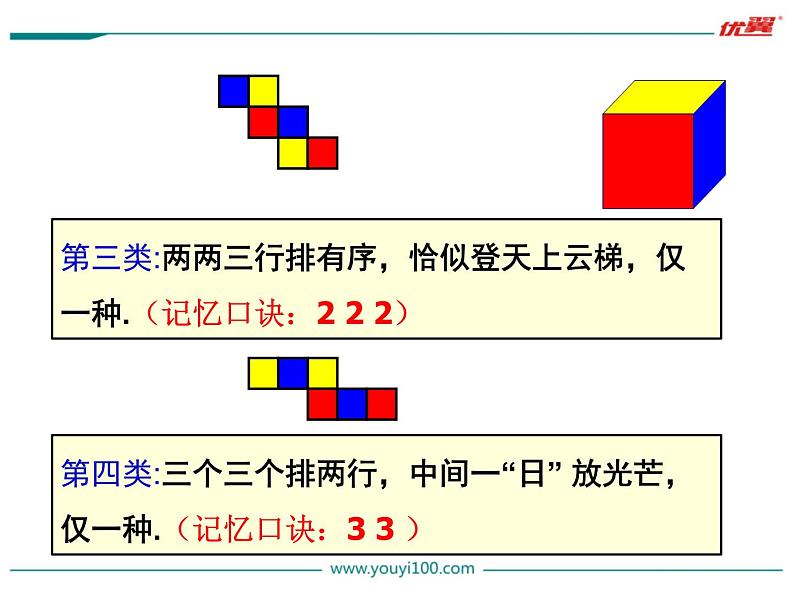
第三类:两两三行排有序，恰似登天上云梯，仅一种.（记忆口诀：2 2 2）
第四类:三个三个排两行，中间一“日” 放光芒， 仅一种.（记忆口诀：3 3 ）
议一议：判断以下几种展开图是否可以折叠成正方体，并说出原因.
说一说：下列的哪个图形能折叠成正方体？
(1)把刚展开的立方体平面图再恢复成立方体； (2)标出相对面的小正方形，可以把相对面用相同字母或相同的颜色或相同的图案来标注；(3)你能发现相对面在展开图上的位置有什么规律吗？
活动3：按下列步骤操作并回答相关问题.
“胜”在上，“利”在前！
例1 如果“你”在前面，那么什么在后面？如果“坚”在下，“就”在后，那么“胜”“利”在哪里？
变式训练1：小红制作了一个如下左图所示的正方体礼品盒，其对面图案都相同，那么这个正方体平面展开图可能是 （ ）
变式训练2：已知一不透明的正方体的六个面上分别写着1至6六个数字，如图是我们能看到的三种情况，那么5的对面数字是____
1.国庆节快到了，准备一个正方体礼盒，六个面分别写有“祝”、“福”、“祖”、“国”、“万”、 “岁”，其中“祝”的对面是“祖”， “万”的对面是“岁”，则它的平面展开图可能是（ ）
2.下列图形可以折成一个正方体形状的盒子.折好以后，与 1 相邻的数是____________，相对的数是______,先 想一想，再具体折一折，看看你的想法是否正确.
将图中的棱柱沿某些棱剪开，展开成一个平面图形，你能得到哪些形状的平面图形？
想一想：以下哪些图形经过折叠可以围成一个棱柱?
思考：你能将图形(1),(3)修改后使其能折叠成棱柱吗?
例2 如图，下列图形经过折叠不能围成一个棱柱的是(　　)
[解析]根据棱柱展开图的特点，棱柱底面边数应该和侧面数相等，因此，应选B.
1.把圆柱的侧面展开，会得到什么图形？
2.把圆锥的侧面展开，会得到什么图形？
想一想: 下面几个图形是一些常见几何体的展开图，你能正确说出这些几何体的名字么？
例3 如图所示是一个五棱柱，它的底面边长都是4 cm，侧棱长都是6 cm.
(1)这个五棱柱共有多少个面？它们分别是什么形状？哪些面的形状、面积完全相同？这个五棱柱共有7个面，其中上、下两个底面，5个侧面．上、下底面都是五边形，侧面都是长方形，上、下底面的形状、面积完全相同.5个侧面的形状、面积完全相同．
(2)这个五棱柱共有多少条棱？它们的长度分别是多少？这个五棱柱共有15条棱，其中5条侧棱的长度都是6 cm，其他棱长都是4 cm.(3)沿一条侧棱剪开将其侧面展成一个平面图形，这个图形是什么形状？面积是多少？将其侧面沿一条棱剪开，展开图是一个长方形，长为4×5＝20(cm)，宽为6 cm，因而面积是20×6＝120(cm2)．
1.下图中，不可能围成正方体的是(　　)
2.将下图中平面展开图折叠成正方体后，相对面上的两个数之和都为6，则x＝____，y＝____．
3.哪种几何体的表面能展开成下面的平面图形？
4.如图所示的纸板上有10个无阴影的正方形，从中选出一个，与图中5个有阴影的正方形一起折一个正方体的包装盒，有多少种不同的选法？
变式训练：如图是一个3×5的方格纸，先将其剪为三部分，是每一部分都可以折成没顶盖的小方盒.问：如何剪？
左边的平面图形可以折叠成右边哪个立体图形?