初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.4 圆周角背景图课件ppt

这是一份初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.4 圆周角背景图课件ppt，共30页。PPT课件主要包含了旧知回放，①角的顶点在圆上，问题探讨，有何发现，探究活动一画一画，探究活动二画一画，探究活动三量一量，探究活动四证一证，验证发现，通过3个分析论证等内容，欢迎下载使用。

2.圆心角的度数和它所对的弧的度数的关系?
3、如图，⊙O中，∠AOB=100º，则AB弧的度数为______，AnB弧的度数为______。
4、判断题： (1)相等的圆心角所对的弧相等 。 (2)等弦对等弧 。 (3)等弧对等弦 。 (4)长度相等的两条弧是等弧 。 (5)平分弦的直径垂直于弦 。
一个周角是360º.把圆周平均分成360份，每一份叫做1°的弧.
1°的弧是指任何一个圆来说的,跟圆的半径的大小无关.
旧知回放:圆心角的定义？
顶点在圆心的角叫圆心角。
思考：你能仿照圆心角的定义， 给下图中象∠ACB 这样的角下个定义吗？
顶点在圆上，并且两边都和圆相交的角叫做圆周角．
② 角的两边都与圆相交.
判断下列图形中所画的∠P是否为圆周角？并说明理由。
顶点在圆上，两边和圆相交。
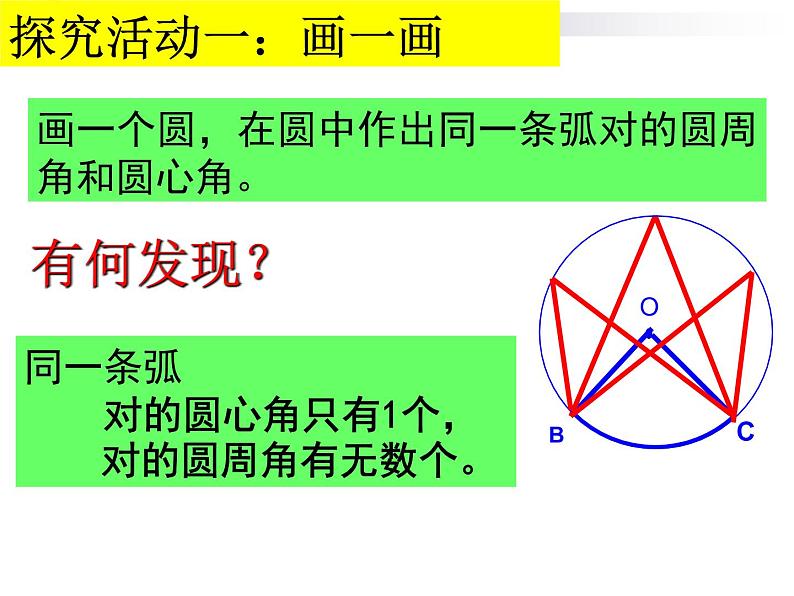
画一个圆，在圆中作出同一条弧对的圆周角和圆心角。
同一条弧 对的圆心角只有1个， 对的圆周角有无数个。
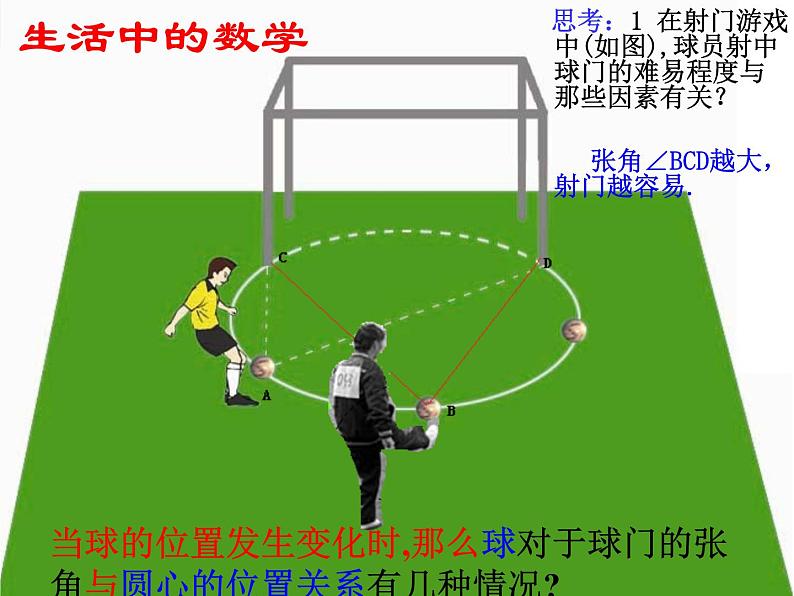
思考：1 在射门游戏中(如图),球员射中球门的难易程度与那些因素有关？ 张角∠BCD越大，射门越容易.
当球的位置发生变化时,那么球对于球门的张角与圆心的位置关系有几种情况?
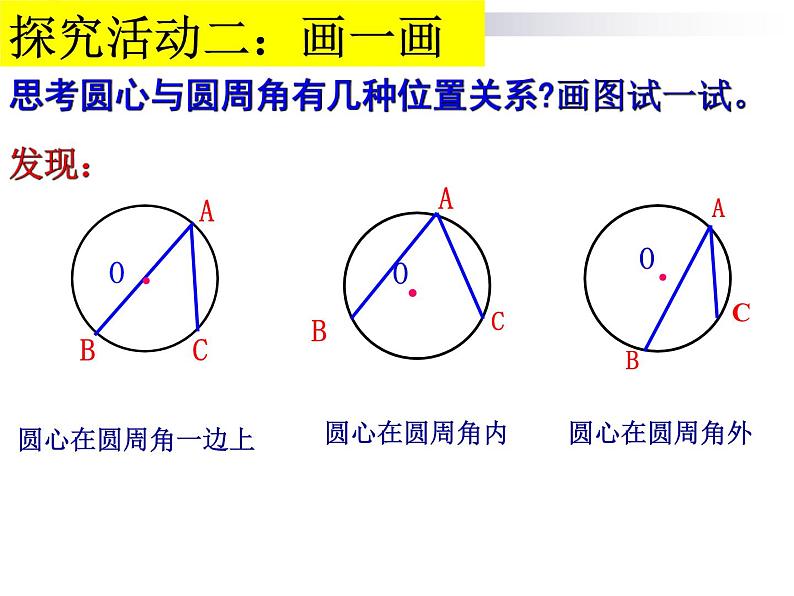
思考圆心与圆周角有几种位置关系?画图试一试。
同一条弧所对的圆周角∠BAC与圆心角 ∠BOC 有什么大小关系？量一量。
同一条弧所对的圆周角等于它所对的圆心角的一半。
如图，在圆O中，求证∠BAC= ∠BOC
分析论证圆周角和圆心角的关系
1.首先考虑一种特殊情况：当圆心(O)在圆周角的一条边上时,圆周角∠ABC与圆心角∠AOC的大小关系.
∵∠AOC是△ABO的外角，
∴∠AOC=∠B+∠A.
同弧所对的圆周角等于它所对的圆心角的一半.
期望:你要理解并掌握这个模型.
如果圆心不在圆周角的一边上,结果会怎样?2.当圆心(O)在圆周角的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
提示你:能否转化为1的情况?
过点B作直径BD.由1可得:
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
老师提示:能否也转化为1的情况?
一条弧所对的圆周角等于它所对的圆心角的一半
思考：圆周角定理的证明过程中，用到了什么数学方法？
在同圆或等圆中，同弧或等弧，所对的圆周角相等，都等于该弧或等弧所对的圆心角的一半；
反之，相等的圆周角所对的弧也相等。
∠ACB= ； ∠ADB= ；∠ =∠ .
推论1:同弧或等弧所对的圆周角都相等
如图，线段AB是⊙O的直径，
点C是⊙O上任意一点（除点A、B），
∠ACB就是直径AB所对的圆周角.
想想看，∠ACB会是怎么样的角？
∵OA＝OB＝OC，
∴△AOC、△BOC都是等腰三角形，
∠OAC＝∠OCA，
∠OAC＋∠OBC＋∠ACB＝180°，
∠ACB＝∠OCA＋∠OCB＝
半圆或直径所对的圆周角都是直角=90°
90°的圆周角所对的弦是圆的直径。
因此，不管点C在⊙O上何处（除点A、B）∠ACB总等于90°，
猜一猜 在射门游戏中(如图), 三名球员站在B、D、E哪个位置较容易射中球门？
比较三个圆周角∠ABC、∠ADC、∠AEC的大小 问题。
如图：OA、OB、OC都是⊙O的半径 ∠AOB=2∠BOC.∠ACB与∠BAC的大小有什么关系？为什么？.
规律:在解决圆周角和圆心角的计算或证明问题时,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理。
分析:AB所对圆周角是∠ACB, 圆心角是∠AOB. 则∠ACB= ∠AOB 同理： ∠ BAC= ∠BOC
已知：如图，在△ABC中，AB=AC,以AB为直径的圆交BC于D,交AC于E,求证：⌒　⌒
∵AB是圆的直径，点D在圆上，
∴AD平分顶角∠BAC，即∠BAD=∠CAD，
（同圆或等圆中，相等的圆周角所对弧相等）。
如图，点A、B、C、D在同一个圆上，四边形ABCD的对角线把4个内角分成8个角，这些角中哪些是相等的角？
方法点拔：由同弧来找相等的圆周角
在同圆或等圆中，如果两个圆周角相等，它们所对弧一定相等吗？为什么？
在同圆或等圆中，如果两个圆周角相等，它们所对弧一定相等．
因为，在同圆或等圆中，如果圆周角相等，那么它所对的圆心角也相等，因此它所对的弧也相等．
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，
同圆或等圆中，两个圆心角、圆心角所对的两条弧、圆心角所对的两条弦中如果有一组量相等，它们所对应的其余各组量也相等。
我发现了…… 我学会了…… 我的体会是…… 我的困难是…… 我……
Summary resnsideratin
归纳：在同圆或等圆中,如果 ① 两个圆心角, ② 两个圆周角 ③ 两条弧, ④ 两条弦, ⑤ 两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.
同圆或等圆中，同弧或等弧所对的圆周角相等；
同圆或等圆中，相等的圆周角所对的弧也相等。
半圆（或直径）所对的圆周角是直角；
用于判断某个圆周角是否是直角
90°的圆周角所对的弦是直径。
用于判断某条线是否过圆心
由特殊到一般和分类讨论的思想。
1：已知⊙O中弦AB等于半径，求弦AB所对的圆心角和圆周角的度数。
2:如图 AB是⊙O的直径, C ,D是圆上的两点,若∠ABD=40°,则∠BCD=＿＿＿＿＿.