

还剩15页未读,
继续阅读
所属成套资源:2020届高三高考数学仿真模拟冲刺卷
成套系列资料,整套一键下载
江西省麻山中学2020届高三高考数学仿真模拟冲刺卷(一)
展开
2020届高考数学仿真模拟冲刺卷(一)
注意事项:
1.本卷仿真文科数学,题序与高考题目序号保持一致,考试时间为120分钟,满分为150分。
2.请将答案填写在答题卷上。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数z满足(i-1)·z=2i(i是虚数单位),则z的共轭复数是( )
A.i-1 B.1+i
C.1-2i D.1-i
2.已知集合M={x|x2=1},N={x|ax=1},若N⊆M,则实数a的取值集合为( )
A.{1} B.{-1,1}
C.{1,0} D.{-1,1,0}
3.下列有关命题的说法错误的是( )
A.若“p∨q”为假命题,则p与q均为假命题
B.“x=1”是“x≥1”的充分不必要条件
C.若p:∃x0∈R,x≥0,则綈p:∀x∈R,x2<0
D.“sin x=”的必要不充分条件是“x=”
4.《九章算术》是我国古代的数学名著,书中把三角形的田称为“圭田”,把直角梯形的田称为“邪田”,称底是“广”,称高是“正从”,“步”是丈量土地的单位.现有一邪田,广分别为十步和二十步,正从为十步,其内有一块广为八步,正从为五步的圭田.若在邪田内随机种植一株茶树,求该株茶树恰好种在圭田内的概率为( )
A. B. C. D.
5.角θ的顶点为坐标原点,始边为x轴正半轴,终边经过点P(4,y),且sin θ=-,则tan θ=( )
A.- B. C.- D.
6.已知直线l:x+y-5=0与圆C:(x-2)2+(y-1)2=r2(r>0)相交所得的弦长为2,则圆C的半径r=( )
A. B.2 C.2 D.4
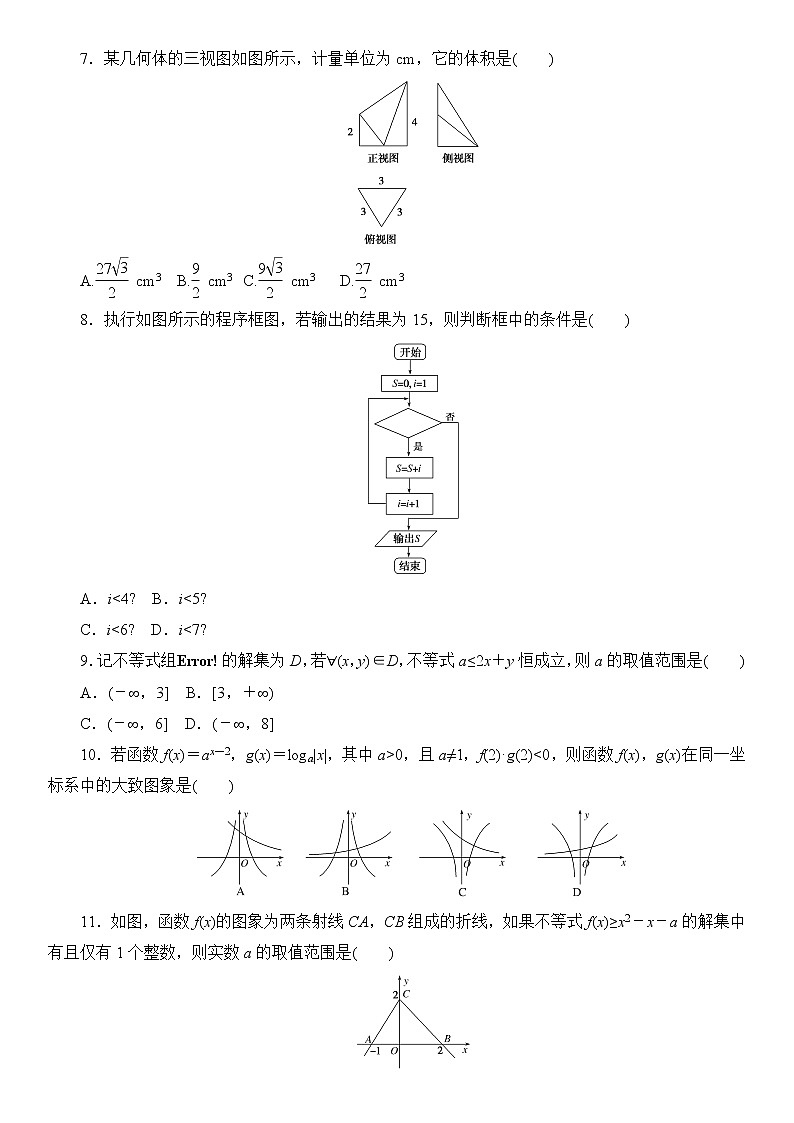
7.某几何体的三视图如图所示,计量单位为cm,它的体积是( )
A. cm3 B. cm3 C. cm3 D. cm3
8.执行如图所示的程序框图,若输出的结果为15,则判断框中的条件是( )
A.i<4? B.i<5?
C.i<6? D.i<7?
9.记不等式组的解集为D,若∀(x,y)∈D,不等式a≤2x+y恒成立,则a的取值范围是( )
A.(-∞,3] B.[3,+∞)
C.(-∞,6] D.(-∞,8]
10.若函数f(x)=ax-2,g(x)=loga|x|,其中a>0,且a≠1,f(2)·g(2)<0,则函数f(x),g(x)在同一坐标系中的大致图象是( )
11.如图,函数f(x)的图象为两条射线CA,CB组成的折线,如果不等式f(x)≥x2-x-a的解集中有且仅有1个整数,则实数a的取值范围是( )
A.{a|-2
12.抛物线y=2x2上有一动弦AB,中点为M,且弦AB的长为3,则点M的纵坐标的最小值为( )
A. B. C. D.1
二、填空题:本题共4小题,每小题5分,共20分.
13.已知向量a与b的夹角为45°,且|a|=1,|b|=,则|a-b|=________.
14.已知f(x)是定义域为R的奇函数,且函数y=f(x-1)为偶函数,当0≤x≤1时,f(x)=x3,则f=________.
15.某同学同时掷两颗均匀的正方体骰子,得到的点数分别为a,b,则椭圆+=1的离心率e>的概率是________.
16.已知数列{an}的前n项和为Sn,对任意n∈N*,Sn=(-1)nan++n-3,且(t-an+1)(t-an)<0恒成立,则实数t的取值范围是____________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)在△ABC中,角A,B,C的对边分别是a,b,c,且asin C=2ccos2.
(1)求角A的大小;
(2)若a=7,△ABC的面积是,求△ABC的周长.
18.(12分)
如图,已知三棱锥P-ABC中,△ABC为等腰直角三角形,AB=AC=1,PB=PC=,设E为PA中点,D为AC中点,F为PB上一点,且PF=2FB.
(1)证明:BD∥平面CEF;
(2)若PA⊥AC,求三棱锥P-ABC的表面积.
19.(12分)已知椭圆C:+=1(a>b>0)的离心率为,短轴长为2.
(1)求椭圆C的标准方程;
(2)设直线l:y=kx+m与椭圆C交于M,N两点,O为坐标原点,若kOM·kON=,求证:点(m,k)在定圆上.
20.(12分)随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,新政策的主要内容包括:①个税起征点为5 000元;②每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;③专项附加扣除包括赡养老人、子女教育、继续教育、大病医疗等、新个税政策赡养老人的扣除标准为每月扣除2 000元,子女教育的扣除标准为每个子女每月扣除1 000元.
新个税政策的税率表部分内容如下:
级数
一级
二级
三级
四级
…
每月应纳税所得额(含税)
不超过3 000元的部分
超过3 000元至12 000元的部分
超过12 000元至25 000元的部分
超过25 000元至35 000元的部分
…
税率(%)
3
10
20
25
…
(1)现有李某月收入19 600元,膝下有一个孩子,李某符合子女教育专项附加扣除、赡养老人专项附加扣除,除此之外,无其他专项附加扣除.请问李某月应缴纳的个税金额为多少?
(2)现收集了某城市50名年龄在40岁到50岁之间的公司白领的相关资料,通过整理资料可知,他们每人至多有一个孩子,符合子女教育专项附加扣除的有40人,不符合子女教育专项附加扣除的有10人,符合子女教育专项附加扣除的人中有30人符合赡养老人专项附加扣除,不符合子女教育专项附加扣除的人中有5人符合赡养老人专项附加扣除,并且他们均不符合其他专项附加扣除(接受统计的这50人中,任何两人均不在一个家庭).若他们的月收入均为20 000元,试求在新个税政策下这50名公司白领的月平均缴纳个税金额为多少?
21.(12分)已知函数f(x)=.
(1)e为自然对数的底数,求函数f(x)的图象在x=处的切线方程;
(2)当x>1时,方程f(x)=a(x-1)+(a>0)有唯一实数根,求a的取值范围.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在平面直角坐标系中,将曲线C1向左平移2个单位长度,再将得到的曲线上的每一个点的横坐标保持不变,纵坐标缩短为原来的,得到曲线C2,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cos θ.
(1)求曲线C2的参数方程;
(2)已知点M在第一象限,四边形MNPQ是曲线C2的内接矩形,求内接矩形MNPQ周长的最大值,并求周长最大时点M的坐标.
23.[选修4-5:不等式选讲](10分)
已知f(x)=|x-2a|+|2x+a|,g(x)=2x+3.
(1)当a=1时,求不等式f(x)<4的解集;
(2)若0
仿真模拟冲刺卷(一)
1.答案:B
解析:z====-i2-i=1-i,所以=1+i,故选B.
2.答案:D
解析:M={x|x2=1}={-1,1},当a=0时,N=∅,满足N⊆M,当a≠0时,因为N⊆M,所以=-1或=1,即a=-1或a=1.故选D.
3.答案:D
解析:当x=时,sin x=成立,所以满足充分条件;当sin x=时,x不一定为,所以必要条件不成立.故D错误,选D.
4.答案:A
解析:由题意可得邪田的面积S=×(10+20)×10=150,圭田的面积S1=×8×5=20,则所求的概率P===.
5.答案:C
解析:因为角θ的终边经过点P(4,y),sin θ=-<0,所以角θ为第四象限角,所以cos θ==,所以tan θ==-,故选C.
6.答案:B
解析:解法一 依题意,圆C的圆心为(2,1),圆心到直线的距离d==,又弦长为2,所以2=2,所以r=2,故选B.
解法二 联立得,整理得2x2-12x+20-r2=0,设直线与圆的两交点分别为A(x1,y1),B(x2,y2),所以x1+x2=6,x1·x2=,所以|AB|=|x1-x2|==2,解得r=2.
7.答案:C
解析:
由三视图可知,该几何体为如图所示的四棱锥S-ABCD,则其体积V=××(2+4)×3×3×=(cm3),故选C.
8.答案:C
解析:由程序框图可知,该程序框图的功能是计算S=1+2+3+…+i=的值,又S=15,所以i=5,当i+1=6时退出循环,结合选项可知,应填i<6?.故选C.
9.答案:C
解析:不等式组表示的平面区域如图中阴影部分所示,设z=2x+y,作出直线2x+y=0并平移,由图知目标函数z=2x+y取得最小值的最优解为(1,4),所以目标函数z=2x+y的最小值为6,因为∀(x,y)∈D,不等式a≤2x+y恒成立,所以a≤6,故选C.
10.答案:A
解析:由题意知f(x)=ax-2是指数型函数,g(x)=loga|x|是对数型函数,且是一个偶函数,由f(2)g(2)<0,可得g(2)<0,故loga2<0,故0
解析:根据题意可知f(x)=,不等式f(x)≥x2-x-a等价于a≥x2-x-f(x),令g(x)=x2-x-f(x)=,作出g(x)的大致图象,如图所示,又g(0)=-2,g(1)=-1,g(-1)=2,∴要使不等式的解集中有且仅有1个整数,则-2≤a<-1,即实数a的取值范围是{a|-2≤a<-1}.故选B.
12.答案:A
解析:由题意设A(x1,y1),B(x2,y2),M(x0,y0),直线AB的方程为y=kx+b.由题意知y0≥b>0.联立得,整理得2x2-kx-b=0,Δ=k2+8b>0,x1+x2=,x1x2=-,则|AB|=,点M的纵坐标y0==x+x=+b.因为弦AB的长为3,所以=3,即(1+k2)=9,故(1+4y0-4b)(y0+b)=9,即(1+4y0-4b)(4y0+4b)=36.由基本不等式得,(1+4y0-4b)+(4y0+4b)≥2=12,当且仅当时取等号,即1+8y0≥12,y0≥,点M的纵坐标的最小值为.故选A.
13.答案:1
解析:因为|a-b|2=|a|2+|b|2-2a·b=12+()2-2×1×cos 45°=1,故|a-b|=1.
14.答案:-
解析:解法一 因为f(x)是R上的奇函数,y=f(x-1)为偶函数,所以f(x-1)=f(-x-1)=-f(x+1),所以f(x+2)=-f(x),f(x+4)=f(x),即f(x)的周期T=4,因为0≤x≤1时,f(x)=x3,所以f=f=f=-f=-f=f=-f=-.
解法二 因为f(x)是R上的奇函数,y=f(x-1)为偶函数,所以f(x-1)=f(-x-1)=-f(x+1),所以f(x+2)=-f(x),由题意知,当-1≤x<0时,f(x)=x3,故当-1≤x≤1时,f(x)=x3,当1
解析:同时掷两颗均匀的正方体骰子,得到的点数分别为a,b,共有6×6种情况.当a>b时,离心率e=>,所以a>2b,符合a>2b的有,,,,,,共6种情况.同理,当a的情况也有6种.综上可知,离心率e>的概率为=.
16.答案:
解析:当n=1时,a1=S1=-a1++1-3,解得a1=-.当n≥2时,an=Sn-Sn-1=(-1)nan++n-3-(-1)n-1an-1--(n-1)+3=(-1)nan-(-1)n-1an-1-+1.若n为偶数,则an-1=-1,
∴an=-1(n为正奇数);若n为奇数,则an-1=-2an-+1=-2-+1=3-,
∴an=3-(n为正偶数).当n为正奇数时,数列{an}为递减数列,其最大值为a1=-1=-,当n为正偶数时,数列{an}为递增数列,其最小值为a2=3-=.若(t-an+1)(t-an)<0恒成立,则-
解法一 所以2sincos=2sin2,又sin≠0,所以cos=sin,所以tan=,易知0
即sin=,
又
由余弦定理,得b2+c2-2bccos A=b2+c2+bc=49,
即(b+c)2-bc=49,
所以(b+c)2-15=49,b+c=8,
故△ABC的周长为a+b+c=15.(12分)
18.解析:(1)如图,连接PD交CE于G点,连接FG,
∵E为PA中点,D为AC中点,
∴点G为△PAC的重心,∴PG=2GD.(2分)
∵PF=2FB,∴FG∥BD.(4分)
又FG⊂平面CEF,BD⊄平面CEF,
∴BD∥平面CEF.(5分)
(2)∵AB=AC=1,PB=PC=,PA=PA,
∴△PAB≌△PAC.
∵PA⊥AC,∴PA==2.(7分)
S△ABC=,S△PAC=1.(9分)
在△PBC中,BC=,PB=PC=,
∴BC边上的高为 =,
∴S△PBC=××=,(11分)
∴三棱锥P-ABC的表面积S表面积=S△ABC+2S△PAC+S△PBC=+2+=4.(12分)
19.解析:(1)设椭圆C的焦距为2c,由已知e==,2b=2,a2=b2+c2,得b=1,a=2,
∴椭圆C的标准方程为+y2=1.(4分)
(2)设M(x1,y1),N(x2,y2),联立得,
(4k2+1)x2+8kmx+4m2-4=0,
依题意,Δ=(8km)2-4(4k2+1)(4m2-4)>0,化简得m2<4k2+1.①
由根与系数的关系得,x1+x2=,x1x2=,(6分)
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
若kOM·kON=,则=,即4y1y2=5x1x2,
∴4k2x1x2+4km(x1+x2)+4m2=5x1x2,
∴(4k2-5)×+4km·+4m2=0,
即(4k2-5)(m2-1)-8k2m2+m2(4k2+1)=0,化简得m2+k2=.②(9分)
由①②得0≤m2<,
20.解析:(1)李某月应纳税所得额(含税)为19 600-5 000-1 000-2 000=11 600(元),(1分)
不超过3 000元的部分月应缴纳的个税金额为3 000×3%=90(元),(2分)
超过3 000元至12 000元的部分月应缴纳的个税金额为8 600×10%=860(元),(3分)
所以李某月应缴纳的个税金额为90+860=950(元).(4分)
(2)符合子女教育专项附加扣除,且符合赡养老人专项附加扣除的人应纳税所得额(含税)为20 000-5 000-1 000-2 000=12 000(元),
月应缴纳的个税金额为90+900=990(元);(5分)
符合子女教育专项附加扣除,不符合赡养老人专项附加扣除的人应纳税所得额(含税)为20 000-5 000-1 000=14 000(元),
月应缴纳的个税金额为90+900+400=1 390(元);(6分)
不符合子女教育专项附加扣除,符合赡养老人专项附加扣除的人应纳税所得额(含税)为20 000-5 000-2 000=13 000(元),
月应缴纳的个税金额为90+900+200=1 190(元);(8分)
不符合子女教育专项附加扣除,且不符合赡养老人专项附加扣除的人应纳税所得额(含税)为20 000-5 000=15 000(元),
月应缴纳的个税金额为90+900+600=1 590(元).(10分)
因为(990×30+1 390×10+1 190×5+1 590×5)÷50=1 150(元),
所以在新个税政策下这50名公司白领月平均缴纳个税金额为1 150元.(12分)
21.解析:(1)函数f(x)的定义域为(0,+∞),
f′(x)=,所以f′=2e4,又f=-e2,(2分)
所以函数f(x)的图象在x=处的切线方程为y+e2=2e4,
即y=2e4x-3e2.(4分)
(2)当x>1时,f(x)=a(x-1)+,即ln x-a(x2-x)=0.
令h(x)=ln x-a(x2-x),有h(1)=0,h′(x)=.(5分)
令r(x)=-2ax2+ax+1(a>0),
则r(0)=1,r(1)=1-a,
①当a≥1时,r(1)≤0,r(x)在(1,+∞)单调递减,所以x∈(1,+∞)时,r(x)<0,即h′(x)<0,所以h(x)在(1,+∞)单调递减,故当x>1时,h(x)
②当00,r(x)在(1,+∞)单调递减,所以存在x0∈(1,+∞),使得x∈(1,x0)时,r(x)>0,即h(x)单调递增;x∈(x0+∞)时,r(x)<0,即h(x)单调递减.(9分)
所以h(x)max=h(x0)>h(1)=0.
取x=1+(x>2),
则h=ln-a2+a=ln-.
令m(t)=ln t-t(t>2),
则m′(t)=-1<0,
所以m(t)在(2,+∞)单调递减,
所以m(t)
综上,a的取值范围为(0,1).(12分)
22.解析:(1)由ρ=4cos θ得曲线C1的直角坐标方程为(x-2)2+y2=4,(2分)
经过变换后的曲线对应的方程为+y2=1,即曲线C2的普通方程,(4分)
∴曲线C2的参数方程为(α为参数).(5分)
(2)设四边形MNPQ的周长为l,点M(2cos α,sin α),
则l=8cos α+4sin α=4=4sin(α+φ),其中cos φ==,sin φ==.(7分)
∵0<α<,∴φ<α+φ<+φ,∴sin
∴2cos α=2sin φ=,sin α=cos φ=,M.(10分)
23.解析:(1)当a=1时,不等式f(x)<4即|x-2|+|2x+1|<4,(1分)
①当x<-时,不等式化为-(x-2)-(2x+1)<4,解得-1
③当x>2时,不等式化为(x-2)+(2x+1)<4,无解.(4分)
综上,不等式f(x)<4的解集为{x|-1
f(x)
所以a的取值范围为.(10分)
注意事项:
1.本卷仿真文科数学,题序与高考题目序号保持一致,考试时间为120分钟,满分为150分。
2.请将答案填写在答题卷上。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知复数z满足(i-1)·z=2i(i是虚数单位),则z的共轭复数是( )
A.i-1 B.1+i
C.1-2i D.1-i
2.已知集合M={x|x2=1},N={x|ax=1},若N⊆M,则实数a的取值集合为( )
A.{1} B.{-1,1}
C.{1,0} D.{-1,1,0}
3.下列有关命题的说法错误的是( )
A.若“p∨q”为假命题,则p与q均为假命题
B.“x=1”是“x≥1”的充分不必要条件
C.若p:∃x0∈R,x≥0,则綈p:∀x∈R,x2<0
D.“sin x=”的必要不充分条件是“x=”
4.《九章算术》是我国古代的数学名著,书中把三角形的田称为“圭田”,把直角梯形的田称为“邪田”,称底是“广”,称高是“正从”,“步”是丈量土地的单位.现有一邪田,广分别为十步和二十步,正从为十步,其内有一块广为八步,正从为五步的圭田.若在邪田内随机种植一株茶树,求该株茶树恰好种在圭田内的概率为( )
A. B. C. D.
5.角θ的顶点为坐标原点,始边为x轴正半轴,终边经过点P(4,y),且sin θ=-,则tan θ=( )
A.- B. C.- D.
6.已知直线l:x+y-5=0与圆C:(x-2)2+(y-1)2=r2(r>0)相交所得的弦长为2,则圆C的半径r=( )
A. B.2 C.2 D.4
7.某几何体的三视图如图所示,计量单位为cm,它的体积是( )
A. cm3 B. cm3 C. cm3 D. cm3
8.执行如图所示的程序框图,若输出的结果为15,则判断框中的条件是( )
A.i<4? B.i<5?
C.i<6? D.i<7?
9.记不等式组的解集为D,若∀(x,y)∈D,不等式a≤2x+y恒成立,则a的取值范围是( )
A.(-∞,3] B.[3,+∞)
C.(-∞,6] D.(-∞,8]
10.若函数f(x)=ax-2,g(x)=loga|x|,其中a>0,且a≠1,f(2)·g(2)<0,则函数f(x),g(x)在同一坐标系中的大致图象是( )
11.如图,函数f(x)的图象为两条射线CA,CB组成的折线,如果不等式f(x)≥x2-x-a的解集中有且仅有1个整数,则实数a的取值范围是( )
A.{a|-2
12.抛物线y=2x2上有一动弦AB,中点为M,且弦AB的长为3,则点M的纵坐标的最小值为( )
A. B. C. D.1
二、填空题:本题共4小题,每小题5分,共20分.
13.已知向量a与b的夹角为45°,且|a|=1,|b|=,则|a-b|=________.
14.已知f(x)是定义域为R的奇函数,且函数y=f(x-1)为偶函数,当0≤x≤1时,f(x)=x3,则f=________.
15.某同学同时掷两颗均匀的正方体骰子,得到的点数分别为a,b,则椭圆+=1的离心率e>的概率是________.
16.已知数列{an}的前n项和为Sn,对任意n∈N*,Sn=(-1)nan++n-3,且(t-an+1)(t-an)<0恒成立,则实数t的取值范围是____________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17.(12分)在△ABC中,角A,B,C的对边分别是a,b,c,且asin C=2ccos2.
(1)求角A的大小;
(2)若a=7,△ABC的面积是,求△ABC的周长.
18.(12分)
如图,已知三棱锥P-ABC中,△ABC为等腰直角三角形,AB=AC=1,PB=PC=,设E为PA中点,D为AC中点,F为PB上一点,且PF=2FB.
(1)证明:BD∥平面CEF;
(2)若PA⊥AC,求三棱锥P-ABC的表面积.
19.(12分)已知椭圆C:+=1(a>b>0)的离心率为,短轴长为2.
(1)求椭圆C的标准方程;
(2)设直线l:y=kx+m与椭圆C交于M,N两点,O为坐标原点,若kOM·kON=,求证:点(m,k)在定圆上.
20.(12分)随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,新政策的主要内容包括:①个税起征点为5 000元;②每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;③专项附加扣除包括赡养老人、子女教育、继续教育、大病医疗等、新个税政策赡养老人的扣除标准为每月扣除2 000元,子女教育的扣除标准为每个子女每月扣除1 000元.
新个税政策的税率表部分内容如下:
级数
一级
二级
三级
四级
…
每月应纳税所得额(含税)
不超过3 000元的部分
超过3 000元至12 000元的部分
超过12 000元至25 000元的部分
超过25 000元至35 000元的部分
…
税率(%)
3
10
20
25
…
(1)现有李某月收入19 600元,膝下有一个孩子,李某符合子女教育专项附加扣除、赡养老人专项附加扣除,除此之外,无其他专项附加扣除.请问李某月应缴纳的个税金额为多少?
(2)现收集了某城市50名年龄在40岁到50岁之间的公司白领的相关资料,通过整理资料可知,他们每人至多有一个孩子,符合子女教育专项附加扣除的有40人,不符合子女教育专项附加扣除的有10人,符合子女教育专项附加扣除的人中有30人符合赡养老人专项附加扣除,不符合子女教育专项附加扣除的人中有5人符合赡养老人专项附加扣除,并且他们均不符合其他专项附加扣除(接受统计的这50人中,任何两人均不在一个家庭).若他们的月收入均为20 000元,试求在新个税政策下这50名公司白领的月平均缴纳个税金额为多少?
21.(12分)已知函数f(x)=.
(1)e为自然对数的底数,求函数f(x)的图象在x=处的切线方程;
(2)当x>1时,方程f(x)=a(x-1)+(a>0)有唯一实数根,求a的取值范围.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.
22.[选修4-4:坐标系与参数方程](10分)
在平面直角坐标系中,将曲线C1向左平移2个单位长度,再将得到的曲线上的每一个点的横坐标保持不变,纵坐标缩短为原来的,得到曲线C2,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的极坐标方程为ρ=4cos θ.
(1)求曲线C2的参数方程;
(2)已知点M在第一象限,四边形MNPQ是曲线C2的内接矩形,求内接矩形MNPQ周长的最大值,并求周长最大时点M的坐标.
23.[选修4-5:不等式选讲](10分)
已知f(x)=|x-2a|+|2x+a|,g(x)=2x+3.
(1)当a=1时,求不等式f(x)<4的解集;
(2)若0
仿真模拟冲刺卷(一)
1.答案:B
解析:z====-i2-i=1-i,所以=1+i,故选B.
2.答案:D
解析:M={x|x2=1}={-1,1},当a=0时,N=∅,满足N⊆M,当a≠0时,因为N⊆M,所以=-1或=1,即a=-1或a=1.故选D.
3.答案:D
解析:当x=时,sin x=成立,所以满足充分条件;当sin x=时,x不一定为,所以必要条件不成立.故D错误,选D.
4.答案:A
解析:由题意可得邪田的面积S=×(10+20)×10=150,圭田的面积S1=×8×5=20,则所求的概率P===.
5.答案:C
解析:因为角θ的终边经过点P(4,y),sin θ=-<0,所以角θ为第四象限角,所以cos θ==,所以tan θ==-,故选C.
6.答案:B
解析:解法一 依题意,圆C的圆心为(2,1),圆心到直线的距离d==,又弦长为2,所以2=2,所以r=2,故选B.
解法二 联立得,整理得2x2-12x+20-r2=0,设直线与圆的两交点分别为A(x1,y1),B(x2,y2),所以x1+x2=6,x1·x2=,所以|AB|=|x1-x2|==2,解得r=2.
7.答案:C
解析:
由三视图可知,该几何体为如图所示的四棱锥S-ABCD,则其体积V=××(2+4)×3×3×=(cm3),故选C.
8.答案:C
解析:由程序框图可知,该程序框图的功能是计算S=1+2+3+…+i=的值,又S=15,所以i=5,当i+1=6时退出循环,结合选项可知,应填i<6?.故选C.
9.答案:C
解析:不等式组表示的平面区域如图中阴影部分所示,设z=2x+y,作出直线2x+y=0并平移,由图知目标函数z=2x+y取得最小值的最优解为(1,4),所以目标函数z=2x+y的最小值为6,因为∀(x,y)∈D,不等式a≤2x+y恒成立,所以a≤6,故选C.
10.答案:A
解析:由题意知f(x)=ax-2是指数型函数,g(x)=loga|x|是对数型函数,且是一个偶函数,由f(2)g(2)<0,可得g(2)<0,故loga2<0,故0
解析:根据题意可知f(x)=,不等式f(x)≥x2-x-a等价于a≥x2-x-f(x),令g(x)=x2-x-f(x)=,作出g(x)的大致图象,如图所示,又g(0)=-2,g(1)=-1,g(-1)=2,∴要使不等式的解集中有且仅有1个整数,则-2≤a<-1,即实数a的取值范围是{a|-2≤a<-1}.故选B.
12.答案:A
解析:由题意设A(x1,y1),B(x2,y2),M(x0,y0),直线AB的方程为y=kx+b.由题意知y0≥b>0.联立得,整理得2x2-kx-b=0,Δ=k2+8b>0,x1+x2=,x1x2=-,则|AB|=,点M的纵坐标y0==x+x=+b.因为弦AB的长为3,所以=3,即(1+k2)=9,故(1+4y0-4b)(y0+b)=9,即(1+4y0-4b)(4y0+4b)=36.由基本不等式得,(1+4y0-4b)+(4y0+4b)≥2=12,当且仅当时取等号,即1+8y0≥12,y0≥,点M的纵坐标的最小值为.故选A.
13.答案:1
解析:因为|a-b|2=|a|2+|b|2-2a·b=12+()2-2×1×cos 45°=1,故|a-b|=1.
14.答案:-
解析:解法一 因为f(x)是R上的奇函数,y=f(x-1)为偶函数,所以f(x-1)=f(-x-1)=-f(x+1),所以f(x+2)=-f(x),f(x+4)=f(x),即f(x)的周期T=4,因为0≤x≤1时,f(x)=x3,所以f=f=f=-f=-f=f=-f=-.
解法二 因为f(x)是R上的奇函数,y=f(x-1)为偶函数,所以f(x-1)=f(-x-1)=-f(x+1),所以f(x+2)=-f(x),由题意知,当-1≤x<0时,f(x)=x3,故当-1≤x≤1时,f(x)=x3,当1
解析:同时掷两颗均匀的正方体骰子,得到的点数分别为a,b,共有6×6种情况.当a>b时,离心率e=>,所以a>2b,符合a>2b的有,,,,,,共6种情况.同理,当a
16.答案:
解析:当n=1时,a1=S1=-a1++1-3,解得a1=-.当n≥2时,an=Sn-Sn-1=(-1)nan++n-3-(-1)n-1an-1--(n-1)+3=(-1)nan-(-1)n-1an-1-+1.若n为偶数,则an-1=-1,
∴an=-1(n为正奇数);若n为奇数,则an-1=-2an-+1=-2-+1=3-,
∴an=3-(n为正偶数).当n为正奇数时,数列{an}为递减数列,其最大值为a1=-1=-,当n为正偶数时,数列{an}为递增数列,其最小值为a2=3-=.若(t-an+1)(t-an)<0恒成立,则-
解法一 所以2sincos=2sin2,又sin≠0,所以cos=sin,所以tan=,易知0
即sin=,
又
由余弦定理,得b2+c2-2bccos A=b2+c2+bc=49,
即(b+c)2-bc=49,
所以(b+c)2-15=49,b+c=8,
故△ABC的周长为a+b+c=15.(12分)
18.解析:(1)如图,连接PD交CE于G点,连接FG,
∵E为PA中点,D为AC中点,
∴点G为△PAC的重心,∴PG=2GD.(2分)
∵PF=2FB,∴FG∥BD.(4分)
又FG⊂平面CEF,BD⊄平面CEF,
∴BD∥平面CEF.(5分)
(2)∵AB=AC=1,PB=PC=,PA=PA,
∴△PAB≌△PAC.
∵PA⊥AC,∴PA==2.(7分)
S△ABC=,S△PAC=1.(9分)
在△PBC中,BC=,PB=PC=,
∴BC边上的高为 =,
∴S△PBC=××=,(11分)
∴三棱锥P-ABC的表面积S表面积=S△ABC+2S△PAC+S△PBC=+2+=4.(12分)
19.解析:(1)设椭圆C的焦距为2c,由已知e==,2b=2,a2=b2+c2,得b=1,a=2,
∴椭圆C的标准方程为+y2=1.(4分)
(2)设M(x1,y1),N(x2,y2),联立得,
(4k2+1)x2+8kmx+4m2-4=0,
依题意,Δ=(8km)2-4(4k2+1)(4m2-4)>0,化简得m2<4k2+1.①
由根与系数的关系得,x1+x2=,x1x2=,(6分)
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
若kOM·kON=,则=,即4y1y2=5x1x2,
∴4k2x1x2+4km(x1+x2)+4m2=5x1x2,
∴(4k2-5)×+4km·+4m2=0,
即(4k2-5)(m2-1)-8k2m2+m2(4k2+1)=0,化简得m2+k2=.②(9分)
由①②得0≤m2<,
20.解析:(1)李某月应纳税所得额(含税)为19 600-5 000-1 000-2 000=11 600(元),(1分)
不超过3 000元的部分月应缴纳的个税金额为3 000×3%=90(元),(2分)
超过3 000元至12 000元的部分月应缴纳的个税金额为8 600×10%=860(元),(3分)
所以李某月应缴纳的个税金额为90+860=950(元).(4分)
(2)符合子女教育专项附加扣除,且符合赡养老人专项附加扣除的人应纳税所得额(含税)为20 000-5 000-1 000-2 000=12 000(元),
月应缴纳的个税金额为90+900=990(元);(5分)
符合子女教育专项附加扣除,不符合赡养老人专项附加扣除的人应纳税所得额(含税)为20 000-5 000-1 000=14 000(元),
月应缴纳的个税金额为90+900+400=1 390(元);(6分)
不符合子女教育专项附加扣除,符合赡养老人专项附加扣除的人应纳税所得额(含税)为20 000-5 000-2 000=13 000(元),
月应缴纳的个税金额为90+900+200=1 190(元);(8分)
不符合子女教育专项附加扣除,且不符合赡养老人专项附加扣除的人应纳税所得额(含税)为20 000-5 000=15 000(元),
月应缴纳的个税金额为90+900+600=1 590(元).(10分)
因为(990×30+1 390×10+1 190×5+1 590×5)÷50=1 150(元),
所以在新个税政策下这50名公司白领月平均缴纳个税金额为1 150元.(12分)
21.解析:(1)函数f(x)的定义域为(0,+∞),
f′(x)=,所以f′=2e4,又f=-e2,(2分)
所以函数f(x)的图象在x=处的切线方程为y+e2=2e4,
即y=2e4x-3e2.(4分)
(2)当x>1时,f(x)=a(x-1)+,即ln x-a(x2-x)=0.
令h(x)=ln x-a(x2-x),有h(1)=0,h′(x)=.(5分)
令r(x)=-2ax2+ax+1(a>0),
则r(0)=1,r(1)=1-a,
①当a≥1时,r(1)≤0,r(x)在(1,+∞)单调递减,所以x∈(1,+∞)时,r(x)<0,即h′(x)<0,所以h(x)在(1,+∞)单调递减,故当x>1时,h(x)
②当0
所以h(x)max=h(x0)>h(1)=0.
取x=1+(x>2),
则h=ln-a2+a=ln-.
令m(t)=ln t-t(t>2),
则m′(t)=-1<0,
所以m(t)在(2,+∞)单调递减,
所以m(t)
综上,a的取值范围为(0,1).(12分)
22.解析:(1)由ρ=4cos θ得曲线C1的直角坐标方程为(x-2)2+y2=4,(2分)
经过变换后的曲线对应的方程为+y2=1,即曲线C2的普通方程,(4分)
∴曲线C2的参数方程为(α为参数).(5分)
(2)设四边形MNPQ的周长为l,点M(2cos α,sin α),
则l=8cos α+4sin α=4=4sin(α+φ),其中cos φ==,sin φ==.(7分)
∵0<α<,∴φ<α+φ<+φ,∴sin
∴2cos α=2sin φ=,sin α=cos φ=,M.(10分)
23.解析:(1)当a=1时,不等式f(x)<4即|x-2|+|2x+1|<4,(1分)
①当x<-时,不等式化为-(x-2)-(2x+1)<4,解得-1
③当x>2时,不等式化为(x-2)+(2x+1)<4,无解.(4分)
综上,不等式f(x)<4的解集为{x|-1
f(x)
所以a的取值范围为.(10分)
相关资料
更多








