甘肃省武威市凉州区和平联片教研组2024-2025学年九年级上学期10月期中数学试题

这是一份甘肃省武威市凉州区和平联片教研组2024-2025学年九年级上学期10月期中数学试题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共30分）
1．（3分）下列图形中，既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
2．（3分）下列方程中，是关于的一元二次方程的是（ ）
A．B．
C．D．
3．（3分）若一元二次方程有实数根，则m的值不可能是（ ）
A．B．C．0D．1
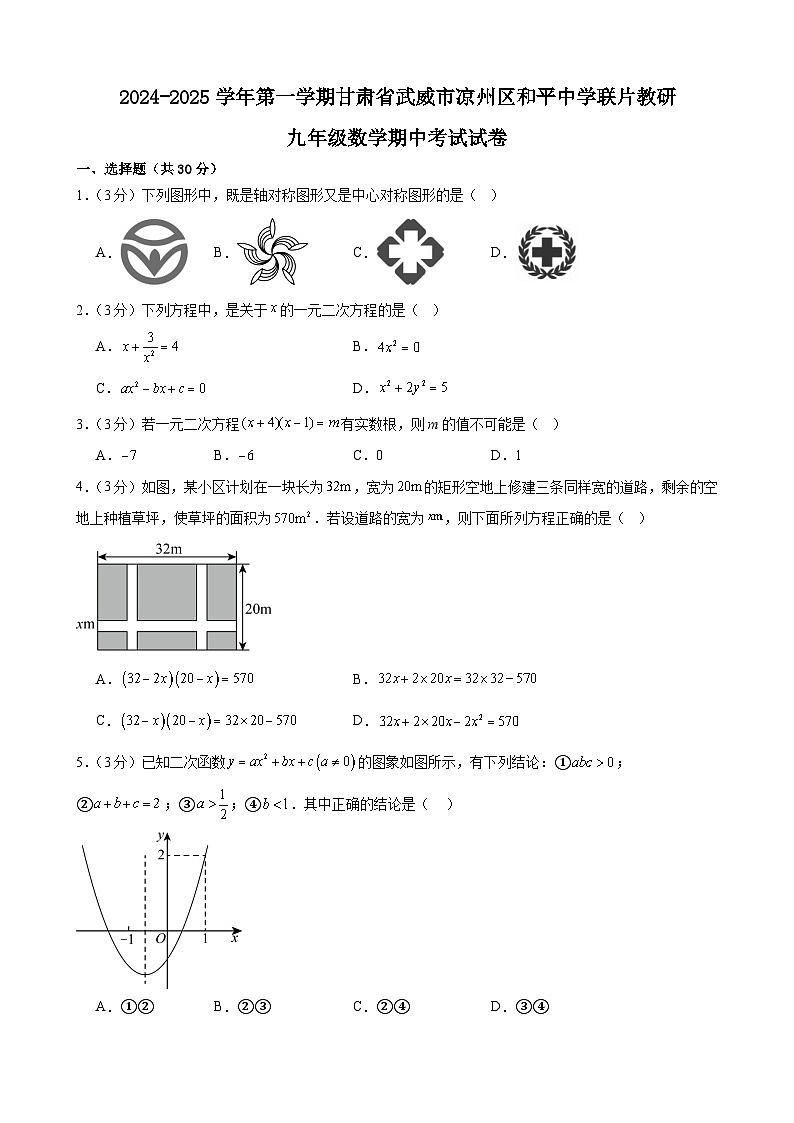
4．（3分）如图，某小区计划在一块长为，宽为的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为．若设道路的宽为，则下面所列方程正确的是（ ）
A．B．
C．D．
5．（3分）已知二次函数的图象如图所示，有下列结论：①；②；③；④．其中正确的结论是（ ）
A．①②B．②③C．②④D．③④
6．（3分）关于二次函数的图象，下列说法正确的是（ ）
A．对称轴是直线B．当时，随的增大而减小
C．最小值是D．图象与轴没有交点
7．（3分）如图，有一矩形纸片，，，将该矩形纸片沿垂直于的三条虚线折成一个上下无盖的长方体纸盒，则长方体纸盒的最大容积为（ ）
A．B．C．D．
8．（3分）如图，将绕B点顺时针方向旋转一个角α到，点A的对应点D恰好落在上，且．若，则α的度数为（ ）
A．30°B．40°C．45°D．36°
9．（3分）已知点与点是关于原点O的对称点，则（ ）
A．B．C．D．
10．（3分）如图，正方形的顶点B、C的坐标分别为0,3，2,0，则点A关于原点O的对称点的坐标为（ ）
A．B．C．D．
二、填空题（共24分）
11．（3分）一元二次方程化为一般形式是 ．
12．（3分）已知m，n，3分别是等腰三角形三边的长，且m，n是关于x的一元二次方程的两个实数根，则k的值为 ．
13．（3分）我市某楼盘2013年房价为每平方米4500元，经过两年连续降价后，2015年房价为3645元．设该楼盘这两年房价平均降低率为x，根据题意可列方程为 ．
14．（3分）若点，都在抛物线上，则线段的长为 ．
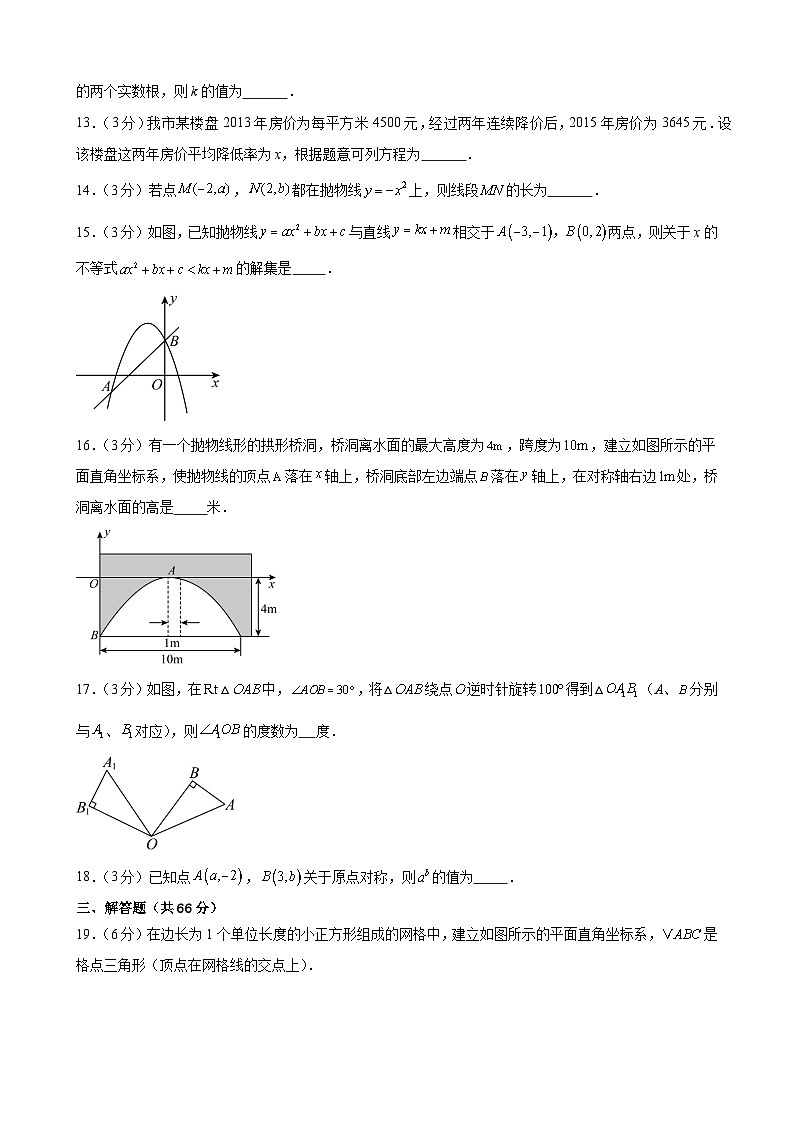
15．（3分）如图，已知抛物线与直线相交于两点，则关于x的不等式的解集是 ．
16．（3分）有一个抛物线形的拱形桥洞，桥洞离水面的最大高度为，跨度为，建立如图所示的平面直角坐标系，使抛物线的顶点落在轴上，桥洞底部左边端点落在轴上，在对称轴右边处，桥洞离水面的高是 米．
17．（3分）如图，在△中，，将△绕点逆时针旋转得到△（A、分别与、对应），则的度数为 度．
18．（3分）已知点，关于原点对称，则的值为 ．
三、解答题（共66分）
19．（6分）在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系，是格点三角形（顶点在网格线的交点上）．
(1)作出关于原点O成中心对称的，并写出点的坐标 ，点的坐标 ；
(2)把向上平移4个单位长度得到，画出；
(3)已知与成中心对称，请直接写出对称中心的坐标．
20．（8分）解方程：
(1)；
(2)（用公式法解）．
21．（6分）已知关于x的一元二次方程，其中a，b，c满足，求满足条件的一元二次方程．
22．（8分）已知 ，是一元二次方程的两个实数根．
(1)求实数的取值范围．
(2)若，满足；求实数的值．
(3)实数在（2）条件下，求代数式的值．
23．（6分）已知二次函数．
(1)求证：不论取何值，该函数图象与轴总有两个交点；
(2)若该函数图象的对称轴是直线，求该函数的图象与轴的交点坐标．
24．（8分）如图，已知正方形的边长为3，E、F分别是AB、边上的点，且，将绕点D按逆时针方向旋转得到．
(1)求证：；
(2)当时，求的长．
25．（6分）如图，在中，，将绕点顺时针旋转得到，点的对应点为，点的对应点落在线段AB上，DE与相交于点，连接．
(1)求证：平分；
(2)若，求的度数．
26．（8分）某商店销售一种商品，平均每周可售出件，每件利润元．为了增加利润，商店准备适当降价，若此商品每降价元，平均每周将多售出件，考虑到运营过程中其它成本，此商品利润不得低于元．
(1)若要使每周销售利润达到元，则此商品每件需要降价多少元？
(2)请问该商品每周的销售利润能达到2000元吗？请说明理由．
27．（10分）如图1，抛物线与x轴，y轴分别交于，B4,0，C三点．

(1)（3分）试求抛物线的解析式；
(2)（3分）若P点在第一象限的抛物线上，连接，当的面积最大时，求点P的坐标．
(3)（4分）点在第一象限的抛物线上，连接．试问，在对称轴左侧的抛物线上是否存在一点P，满足？如果存在，请求出点P的坐标；如果不存在，请说明理由．
答案
11．；12．5或6；13．；14．4；15．或x>0
16．；17．70；18．
19．（1）解：如图，为所求作的三角形；
根据图可知，，；
（2）解：如图，为所求作的三角形；
（3）解：连接、，则、的交点即为对称中心，
∵，，
∴对称中心的坐标为，
即对称中心的坐标为0,2．
20．(1)，
(2)，
21．满足条件的一元二次方程为或
22．(1)；(2)；(3)
23．（1）解：∵
∴
∵
∴
∴不论取何值，该函数图象与轴总有两个交点；
（2）解：∵该函数图象的对称轴是直线，
∴对称轴为直线
∴
∴
∴当时，
∴该函数的图象与轴的交点坐标为．
24．（1）证明：∵四边形为正方形，
∴，，
根据旋转的性质，可知：，
∴，，，
∴，
∴点、、共线，
∵，
∴，
∵，
∴，
∴，
又∵，，
∴，
∴；
（2）解：设，
∵，，
∴，，
∴，
∴，
∵，
∴在中，有，
∴，
解得，
即．
25．（1）证明：绕点顺时针旋转得到，点的对应点为，点的对应点落在线段AB上，
，，
，
，
平分．
（2）解：，，
，
，
，
绕点顺时针旋转得到，
，，，
，
．
26．（1）解：设此商品每件需要降价元，
由题意得，，
解得，，
∵商品利润不得低于元，
∴，
即，
∴不合，舍去，
∴，
答：此商品每件需要降价元；
（2）解：能，理由如下：
当时，
方程整理得，，
解得，（不合，舍去），
∴当每件需要降价10元时，该商品每周的销售利润能达到2000元．
27．（1）解：把，B4,0，代入，得：
，解得：，
∴；
（2）∵，当时，，
∴，
设直线的解析式为：，把B4,0，代入，得：，
∴，
过点作轴，交于点，设，则，

∴，
∴；
∴当时，有最大值，此时；
（3）存在，
∵，
∴抛物线的对称轴为直线，当时，，
∴，
∵，
∴轴，，
∵B4,0，
∴，
∴，
∵轴，
∴，
∴，
设直线与轴交于点，如图，

∵，，，
∴，
∴，
∴，
同（2）可得，直线的解析式为：，
联立，解得：或，
∴．
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
A
B
D
B
B
A
C